Abstract
- Introduction
- 1. Theme urgency
- 2. Goal and tasks of the research
- 3. Theoretical information
- 3.1 Basic definitions and notations
- 3.2 Presentation of oriented graphs
- 3.3 An algorithm for constructing a regular expression
- Conclusion
- References
Introduction
Currently, relevant tasks related to the analysis and synthesis of languages represented in the columns labeled graphs. Interest in the study of these graphs caused by the fact that there are a number of important tasks that are naturally presented in the form of labeled graphs. These graphs have been studied intensively in the verification program and a mobile robot motion planning [1].
Properties of the languages that can be represented by graphs with labeled arcs studied Kleene. He proposed a very well-known algebra describes those languages. Currently, a number of algorithms known to describe these languages and Kleene algebra construction of graphs on this description [2]. It has been proposed algebra similar Kleene algebra to describe languages generated by such graphs, and algorithms of transition from algebraic expressions, describing languages, representing them in graphs and vice versa. It has also been developed and an algorithm for constructing a regular expression for a given labeled graphs [1]. In this paper, we propose to improve the above algorithm to find patterns in the structure and construction of graphs of regular expressions for them.
1. Theme urgency
At this moment there are two types of algorithms for constructing regular expressions for labeled graphs: A) solution of linear equations; B) conversion of the graph. The idea of the transformation of the graph, which consists in reducing its vertices and edges, It was first presented in the book Hopcroft "Introduction to Automata Theory, Languages and Computing" [2]. The method of successive removal of vertices, as well as a method for solving systems of linear equations to construct a regular expression is complex. The difficulty is, if this method is used on a large graph, the growing number of iterations performed by the algorithm. The number of iterations of the algorithm depends on the order the removal of vertices and arcs. The problem of optimal removal of tops and arcs are still not solved. Nogina NV He proposed to exclude those peaks, which are transient in the final [1].
Master's thesis is devoted to actual scientific problem of constructing a regular expression for a given labeled graphs and improvement of an existing algorithm.
2. Goal and tasks of the research
The aim of this work is to identify qualifying special cases subgraphs for which the order is proposed effective removal of vertices and arcs. These methods are heuristic methods for constructing regular expressions.
The main objective of this work is to improve the programming and implementation of the algorithm for constructing a regular expression for a given graph.
Object of research: the construction of a regular expression for a given labeled graph
Subject of research: method of constructing a regular expression for a given labeled graph, based on a consistent reduction of the vertices of the graph.
3. Theoretical information
3.1 Basic definitions and notations
Graph - a collection of objects with links between them. Objects are considered as vertices or nodes of the graph, and communications - as arcs or edges. For different types of uses graphs may differ orientability, restrictions on the number of links and additional data on vertices or edges. A large number of structures that have practical value in mathematics and computer science can be represented by graphs. Graph G - is an ordered pair G = (V; E), for which the following conditions: V - the set of vertices or nodes E - set of pairs (in the case of an undirected graph - unordered) vertices, called edges V and E are generally considered finite sets . The main elements of a graph consists of nodes of the graph, the graph edges and arcs. The combination of these elements defines the concept: an undirected graph, directed graph, and a mixed graph.
Undirected graph - a graph for each edge is immaterial order of its two end-nodes. Directed graph - a graph for each edge which is essentially the order of its two end-nodes. Mixed graph - a graph that contains both oriented and non-oriented edge. Any of these types of graph may comprise one or more ribs, in which both ends meet at a vertex, such ribs are called loops. If a pair of vertices is connected by several edges or arcs in one direction, then the edge (arc) is called multiple (parallel). Arc or edge connects a vertex to itself is called a loop. Graph without loops and multiple arcs called simple.
Arcs with common terminal vertices are called adjacent. The path (or loop) is called simple if ribs therein are not repeated; elementary if it simple and peaks therein are not repeated. Oriented path in a digraph is a finite sequence of vertices V i, for which all pairs (Vi, V i + 1) is the (oriented) edges. Path length (mashrut) in a weighted graph is the sum of the lengths of the links of the way (mashrut).
K number of edges in a path called the length of the path. It is said that this path connects the vertices v1 and vk +1 or leads from the top to the top v1 vk + 1.Putem length of 0 is considered to be a sequence consisting of a single vertex. The way in which all the edges are distinct is called a chain. The way in which all intermediate vertices are distinct is called a simple chain. The path is called a cycle if it first and last vertices are the same.
Labeled graph is said to be eight G = (Q, E, X, Y, μ, π, q0, F), where Q – a finite set of vertices, E – set of arcs, X – set of stamps of vertices, Y – set of stamps of arcs, μ: Q → X – marking function of vertices, π: L → Y – marking function of of arcs, q0 – the initial vertex, F – the set of final vertices.
Let Pre(qi) – set of initial vertices of arcs, incoming to qi, Post(qi) – set of dinal vertices of arcs, outgoing from qi.
Transient vertex is called q ≠ q0,it had Pre(q)= Æ, hanging – q ≠ fin,in which Post(q)=Æ.
Let Z the set of all non-empty words of the form. Consider algebra, ⊛,, wherein the operations on the languages L1, L2, L Í Z+ defined as follows::
1) union operation: V;
2) joint operation: °;
3) operation iteration (loop): L⊛ =, where L0= LinitialLfinal, at that Linitial={x| xw=L, x=X}, Lfinal= {x|w’=L,x=X}; L1=L; Ln+1=Ln◦L for all n≥1.
Regular expressions define inductively:
1) empty set Æ is the regular expression;
2) x, xyx’ Is a regular expression for all characters x,x’=X, y = Y;
3) ifpи qregular expressions, the expressions p◦q, pq, p⊛ as they are regular.
3.2 Presentation of oriented graphs
To represent directed graphs can be used various data structures. Selection depends on the data structure operators to be applied to the top and the arcs of the digraph. One of the most common representations of the digraph G = (V, E) is the adjacency matrix. Suppose that the set of vertices V = {1, 2, ..., n}. The adjacency matrix for the digraph G - is the matrix and the range n x n with a boolean value, where A[i] [j] = true if and only if there is an arc from vertex i to vertex j. Often, the adjacency matrix is true is replaced by 1 and the false - to 0. The access time to the elements of the adjacency matrix depends on the size the set of vertices and a set of arcs. Submission of a digraph adjacency matrix is conveniently used in the algorithms that often need to check for the existence of the arc.
Described generally digraph representation using adjacency matrix can be considered view labeled digraph as by the adjacency matrix, but where element A[i][j] is equal to the label of the arc i>j.
If an arc from i vertex to vertex j does not exist, then the value of A[i][j] can be any value permissible tags, and can be seen as "empty" cell.
Below (pic.1) shows the adjacency matrix for the labeled digraph, who was depicted earlier.
There arc presented Tagged character type, and a space is used in the absence of arcs. The main drawback of the adjacency matrix is that it requires O(N2) the memory capacity, even if the arc substantially less than n2. So read matrix or finding it necessary element requires time on the order O(n2), which does not allow to create algorithms with time O(n) to work with digraphs having order O(n) edges.
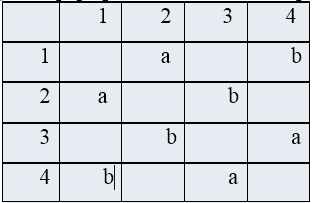
Picture 1 – Adjacency matrix
3.3 An algorithm for constructing a regular expression
Graph G with marked vertices, with initial and final vertices.
Out.The regular expression language generated by the original graph.
Step 1. Graph Gconverted into a graph with marked arcs. To do this, mark the vertices and arcs are erased (qi, ei, qj) markei becomes xiyixj, where xk=m(qk), wherek=i,j, yi=ρ(ei).
The list of vertices introduced fictitious final vertex fin, and a list of arcs – the arc of each final vertexqi to the top fin marked vertex qi.
Step 2. Removal of transient and pendant vertices.
While in the graph there is a vertex q ≠ q0, in which Pre(qi)=Æ do
Delete vertex qiand all arcs emanating from it;
While in the graph there is a vertex qi≠ fin, in whichPost(qi) = Æ do
Delete vertex qi and all arcs incoming to it;;
Step 3. If Graph there is at least one loop or there are peaks that are not initial, of which at least one arc starts, then goto Step 4
else goto Step 7;
Step 4. Deleting multiple arcs and loops.
1. Remove multiples arcs and replaces them with a single arc mark, equal union & shy; pared marks the starting arcs.
2. Remove all loops the next rule.
Let the top qi has a loop with a mark А. If the vertex of the arc in no other vertex, then the loop is removed. The Otherwise, all the arcs (qi, ei, qj), where i≠j, marked arc В, the loop is removed, and the markВ is replaced by the mark А⊛, В ○ В.
On steps 5 – 6 removes one vertex.
Step 5.
Choose qi = Pre(fin);
q := qi;
Step 6.
If q ¹ q0 then remove the top of the q and all incoming and arc extending therefrom. If this is an arbitrary path from a vertex q i in top of the q k , leaving through the top of the q , where q j belongs Pre(q) and q k belongs Post(q), in the graph added arc with & shy; holding a note equal to gluing marks deleted arcs of the path;
goto Step 2;
else qi equal q0 It is not excluded;
choose qm =Pre(q0);
q := qm;
goto 6;
Step 7. Remove all vertices q != q0 and q != fin and all the included arc. We obtain a graph consisting of two vertices: q0 and fin and arcs,between them markedR, where R – this required regular expression.
There is an algorithm(pic.2):
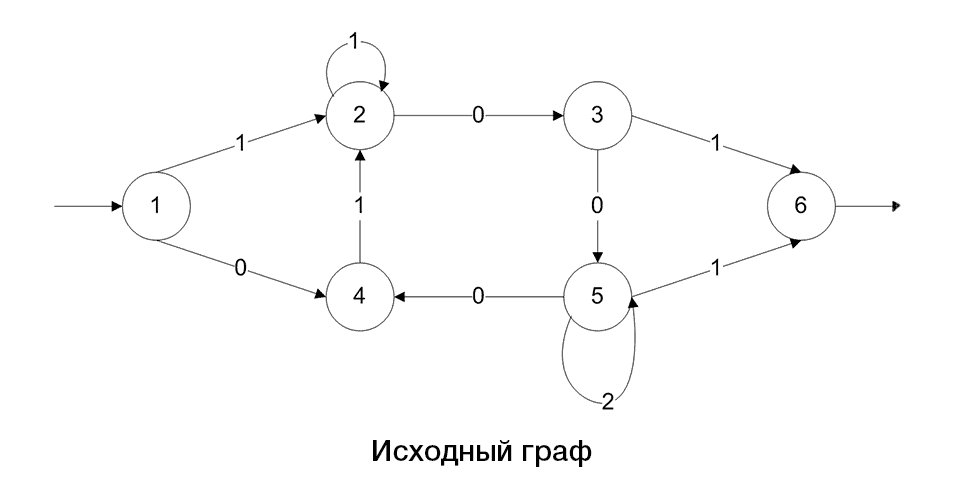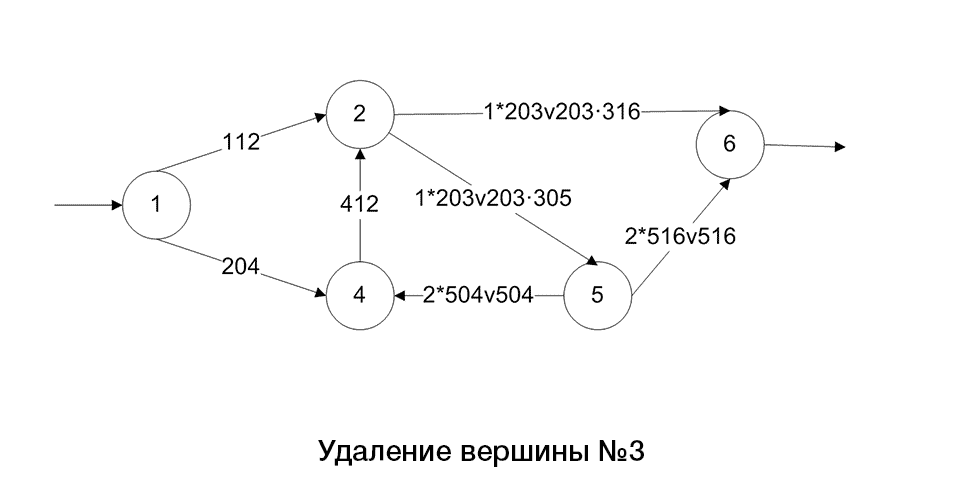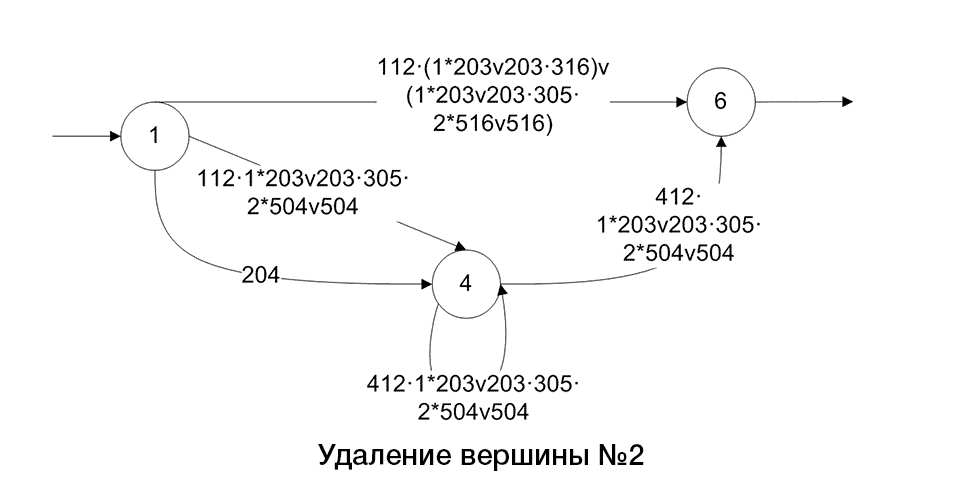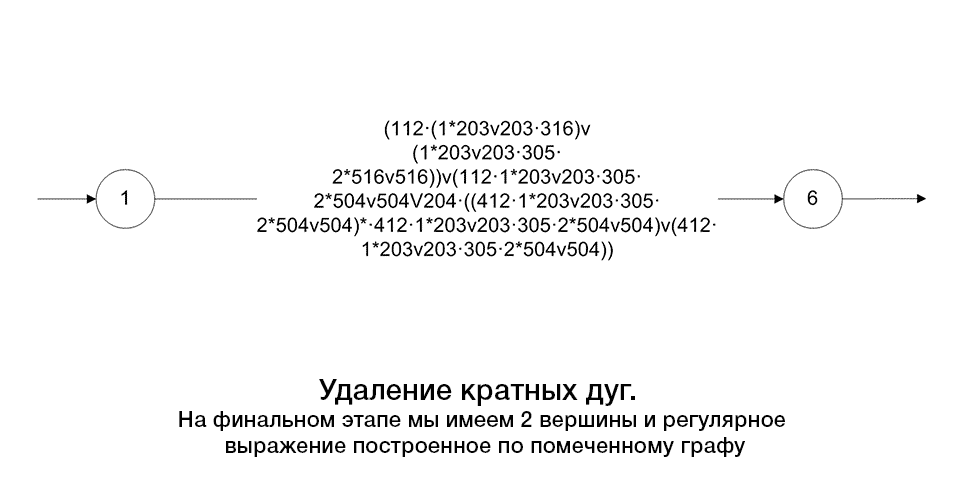
Picture 2 – The algorithm graph transformation by reducing its arcs and vertices
(animation: 10 frames, 5 cycles, 108 KB)
Conclusion
Optimization algorithm for constructing a regular expression on the labeled graph is relevant today.
In this master's work will be to explore different kinds of subgraphs, as well as the best ways to reduce them. As part of the research carried out:
1. The proposed algorithm is analyzed Nogina N.V.
2. Based on the above algorithm was implemented manual errors on different kinds of graphs.
In writing this essay master's work is not yet complete. Final completion: December 2015. The full text of work and materials on the topic can be obtained from the author or his manager after that date.
References
- Ногина Н.В., Грунский И.С. - Синтез регулярного выражения языка,порожденного помеченным графом,методом его локальной редукции, 2012.
- Хопкрофт Д. Введение в теорию автоматов, языков и вычислений / Д. Хопкрофт, Р. Мотвани, Д. Ульман. – М.: Издательский дом «Вильямс», 2002. – 528 с.
- Кристофидес, Н. Теория графов: алгоритмический подход / Н. Кристофидес. – М.: Мир, 1978. – 430 с.
- Ахо А. Построение и анализ вычислительных алгоритмов / А. Ахо, Дж. Хопкрофт, Дж. Ульман. – М.: Мир, 1979. – 536 с.
- Батищев Д.И. Многоуровневая декомпозиция гиперграфовых структур / Батищев Д.И., Старостин Н.В., Филимонов А.В. // Прилож. к журналу «Информационные технологии» №5(141). – М.: Новые технологии. – 2008. – 32 с.
- Ногина Н.В. Построение кратчайшего пути в помеченном графе при помощи локальной редукции графа / Н.В. Ногина, А.В. Билык // Сучасна інформаційна Україна: інформатика, економіка, філософія: матеріали доповідей конференції, 26 квітня 2012 року. – Донецьк, 2012. – 316 с. – С. 76-79.
- Бєлов В.Теорія графів / Бєлов В.– М. : Питер,1968. – 304 с.
- Полат Е.С. Новые педагогические и информационные технологии / Полат Е.С. – М. : Akademia, 1999. – 401с.
- Кузнєцов О.П. Дискретная математика для инженера / Кузнєцов О.П. – М. : Энергоатомиздат, 1988. – 703 с.
- Оре О. Теорія графів / Оре О. – М. : Наука, 1980. – 340 с.
- Смольяков Е.Р. Введение в теоpию гpафов / Смоляков Е.Р. – М. : МГТУ, 1992. – 705 с.
- Hечепуpенко М.И. Алгоpитмы и пpогpаммы pешения задач на гpафах и сетях / Hечепуpенко И.М. – М. : Hаука, 1990. – 202 с.
- Романовский И.В. Алгоpитмы pешения экстpемальных задач / Романовский И.В. – М. : Hаука, 1977. – 506 с.
- Землянухин В.Н. Задачи оптимизации на графах / В.Н. Землянухин, Л.Н. Землянухина. – М. : Наука, 2009. – 677 с.
- Евстигнеев В.А. Графы в программировании: обработка, визуализация и применение / В.А. Евстигнеев, В.Н. Касьянов. – М. : Наука, 1999. – 266 с.
- Новиков Ф.А. Дискретная математика / Новиков Ф.А. – М. : Питер, 2001. – 301 с.
- Алгоритмы на графах [Электронный ресурс] - http://www.chasolimp.de/alggraph_prac.htm