Русский   English
ДонНТУ   Портал магістрів

Реферат за темою випускної роботи

Зміст

Вступ

В даний час актуальні задачі, пов'язані з аналізом і синтезом мов, які представлені у помічених графах. Інтерес до вивчення таких графів викликаний тим, що існує ряд важливих завдань, які природним чином представляються у вигляді позначених графів. Такі графи інтенсивно вивчаються при верифікації програм та плануванні руху мобільного робота [1].

Властивості мов, представимо графами із зазначеними дугами, вивчалися С. Кліні. Ним запропонована широковідома алгебра, що описує ці мови. В даний час відомий ряд алгоритмів опису цих мов в алгебрі Кліні та побудова графів по такому опису [2]. Були запропоновані алгебри, аналогічні алгебрі Кліні, для опису мов, породжених такими графами, і алгоритми переходу від алгебраїчних виразів,   описують мови, до представляють їх графам і навпаки. Також був розроблений і запропонований алгоритм побудови регулярного виразу за заданим позначеного графу [1]. У даній роботі пропонується удосконалити вищевказаний алгоритм, знайти закономірності в будові графів і побудові регулярного виразу по ним.

1. Актуальність теми

На даний момент існує два типи алгоритмів побудови регулярного виразу по позначеному графу: А) рішення системи лінійних рівнянь; Б) перетворення графа. Ідея перетворення графа, яка полягає в скороченні його вершин і дуг, вперше була викладена в книзі Хопкрофта "Введение в теорию автоматов, языков и вычислений" [2]. Метод послідовного видалення вершин, як і метод розв'язання систем лінійних рівнянь для побудови регулярного виразу, є досить складним. Складність полягає в тому що якщо цей метод застосовується на великих графах, то зростає кількість ітерацій виконуваного алгоритму. Кількість ітерацій алгоритму залежить від порядку видалення вершин і дуг. Завдання оптимального видалення вершин і дуг досі не вирішена. Ногіна Н.В. запропонувала виключати ті вершини, які є минущими у фінальну [1].

Магістерська робота присвячена актуальній науковій задачі побудови регулярного виразу за заданим позначеного графу та удосконаленню вже існуючого алгоритму.

2. Мета і задачі дослідження та заплановані результати

Метою даної кваліфікаційної роботи є виділення окремих випадків подграфов, для яких пропонується порядок ефективного видалення вершин і дуг. Ці методи є евристичними методами побудови регулярного виразу.

Основним завданням даної роботи є удосконалення та програмна реалізація алгоритму побудови регулярного виразу за заданим графу.

Об'єкт дослідження: побудова регулярного виразу за заданим позначеного графуя

Предмет дослідження: метод побудови регулярного виразу за заданим позначеного графу, заснований на послідовній редукції вершин графа.

3. Теоретичні відомості

3.1 Основні визначення та позначення

Граф – це сукупність об'єктів із зв'язками між ними. Об'єкти розглядаються як вершини, або вузли графу, а зв'язки – як дуги, або ребра. Для різних областей використання види графів можуть відрізнятися орієнтовністю, обмеженнями на кількість зв'язків і додатковими даними про вершини або ребра. Велика кількість структур, які мають практичну цінність в математиці та інформатиці, можуть бути представлені графами. Граф G – це впорядкована пара G = (V;E), для якої виконуються наступні умови: V –множина вершин або вузлів; E – множина пар (у випадку неорієнтованого графа – невпорядкованих) вершин, які називають ребрами.V і E зазвичай вважаються скінченними множинами. Основні елементи графа складаються з вершин графу, ребер графу та дуг графу. Сполучення цих елементів визначає поняття: неорієнтований граф, орієнтований граф та змішаний граф. Неорієнтований граф – це граф , для кожного ребра якого несуттєвий порядок двох його кінцевих вершин.

Орієнтований граф – це граф, для кожного ребра якого істотний порядок двох його кінцевих вершин. Змішаний граф – це граф, що містить як орієнтовані, так і неорієнтовані ребра. Кожної з перерахованих видів графа може містити одне або кілька ребер, у яких обидва кінці сходяться в одній вершині, такі ребра називаються петлями .

Якщо пара вершин сполучається кількома ребрами чи дугами одного напрямку, то ребра (дуги) називають кратними (паралельними). Дуга чи ребро що сполучає вершину саму із собою називається петлею. Граф без кратних дуг і петель називається простим. Ступінь вершини – кількість ребер графа G, інцидентних вершині x. Вага ребра – значення, поставлено у відповідність даному ребру зваженого графа . Зазвичай вага – дійсне число, в такому випадку його можна інтерпретувати як "довжину" ребра.

Граф, у якому кожному ребру (кожній дузі) поставлено у відповідність певне невід'ємне число, яке називають вагою або довжиною ребра (дуги), називають зваженим графом. Шляхом у графі називають кінцеву послідовність вершин, в якій кожна вершина з'єднана ребром з наступною в послідовності вершин. Дуги, які мають спільні кінцеві вершини, називаються суміжними. Шлях (або цикл) називають простим, якщо ребра в ньому не повторюються; елементарним, якщо він простий і вершини в ньому не повторюються.

Орієнтованим шляхом в Орграф називають кінцеву послідовність вершин V i, Для якої всі пари (Vi,V i + 1) є (орієнтованими) ребрами. Довжиною шляху (машруту) у зваженому графі називають суму довжин ланок цього шляху (машруту). Кількість k ребер у шляху називається довжиною шляху. Кажуть, що цей шлях з’єднує вершини v1 і vk +1 або веде з вершини v1 у вершину vk +1. Шляхом довжини 0 вважається послідовність, що складається з єдиної вершини. Шлях, в якому всі ребра попарно різні, називається ланцюгом. Шлях, в якому всі проміжні вершини попарно різні, називається простим ланцюгом. Шлях називають циклом, якщо в ньому перша та остання вершини збігаються.

Поміченим графом назвемо вісімку G = (Q, E, X, Y, μ, π, q0, F), де Q – множина фінальніх вершин, E – множина дуг, X – множина отметок вершин, Y – множина отметок дуг, μ: Q → X – функція розмітки вершин, π: L → Y – функція розмітки дуг, q0 – початкова вершина графа, F – множина фінальных вершин.

Нехай Pre(qi) – множина початкових вершин всех дуг, входящих в qi, Post(qi) – множина фінальних вершин усіх дуг, вихідних з qi.

Скороминущою вершиною назвемо вершину q ≠ q0, у якої Pre(q)= Æ, висячої – q ≠ fin,у якої Post(q)=Æ.

Пусть Z множина усіх непорожніх слів вида. Розглянемо алгебру, ⊛,, у якій операції на мовах L1, L2, L Í Z+ визначені наступним чином:

1) операція об'єднання: V;

2) операція зчленування (склеювання): °;

3) операція ітерації (зациклення): L⊛ =, где L0= LпочLфін, причем Lпоч={x| xw=L, x=X}, Lфін= {x|w’=L,x=X}; L1=L; Ln+1=Ln◦L для усіх n≥1.

Регулярні вирази визначимо індуктивно:

1) порожня множина Æ є регулярним виразом;

2) x, xyx’ Є регулярними виразами для всіх символівx,x’=X, y = Y;

3) якщо pи qрегулярні вирази, то вирази p◦q, pq, p⊛ також є регулярними.

3.2 Подання графів. Матриця суміжності

Для представлення орієнтованих графів можна використовувати різні структури даних. Вибір структури даних залежить від операторів, які будуть застосовуватися до вершин і дуг орграфа. Одним з найбільш загальних уявлень орграфа G = (V, Е) є матриця суміжності. Припустимо, що множини вершин V = {1, 2, ..., n}. Матриця суміжності для орграфа G - це матриця А розмі-ра n х n зі значеннями булевого типу, де A [i] [j] = true тоді і тільки тоді, коли існує дуга з вершини i в вершину j. Часто в матрицях суміжності значення true замінюється на 1, а значення false - на 0. Час доступу до елементів матриці суміжності залежить від розмірів безлічі вершин і безлічі дуг. Подання орграфа у вигляді матриці суміжності зручно застосовувати в тих алгоритмах, в яких треба часто перевіряти існування даної дуги.

Узагальненням описаного уявлення орграфа за допомогою матриці суміжності можна вважати уявлення поміченого орграфа також за допомогою матриці суміжності,   але у якої елемент А [i] [j] дорівнює мітці дуги i> j.

Якщо дуги від верші¬ни i   до вершини j не існує, то значення A [i] [j] не може бути значенням якої-небудь   допустимої мітки, а може розглядатися як "порожня" осередок.

Нижче (рис. 1) показана матриця суміжності для поміченого орграфа, який був зображений раніше.

Тут дуги представлені міткою символьного типу, а пробіл використовується при відсутності дуг. Основний недолік матриць суміжності полягає в тому, що вона вимагає? (N2) обсягу пам'яті, навіть якщо дуг значно менше, ніж n2. Тому для читання мат¬ріци або знаходження   в ній необхідного елемента потрібен час порядку O (n2), що не дозволяє створювати   алгоритми з часом O (n) для роботи з орграфа, що мають порядку O (n) дуг.

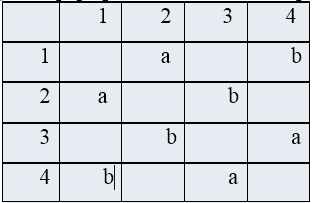
Алгоритм преобразования графа, путем сокращения его дуг и вершин

Рисунок 1 – Матриця суміжності

3.3 Алгоритм побудови регулярного виразу

Вхід. Граф Gіз зазначеними вершинами, Сначальное і фінальними вершинами.

Вихід.Регулярний вираз мови, породженого вихідним графом.

Крок 1. Граф Gперетворюється в граф із зазначеними дугами. Для цього позначки вершин стираються і в дугах (qi, ei, qj)відміткою ei стає xiyixj, де xk=m(qk), де k=i,j, yi=ρ(ei).

У список вершин вводиться фіктивна кінцева вершина fin, а в список дуг & ndash; дуга з кожної фінальної вершини qi в вершину fin з відміткою вершини qi.

Крок 2. Видалення минущих і висячих вершин.

While в графі існує вершина q ≠ q0, у якої Pre(qi)=Æ do

видаляємо вершину qiі всі дуги, що виходять з неї;

While в графі існує вершина qi≠ fin, у якої Post(qi) = Æ do

Видаляємо вершину qi і всі дуги, які входять до неї;

Крок 3. If в графі існує хоч одна петля або існують вершини, що не є початковими, з яких виходить хоч одна дуга, then goto Крок 4

else goto Крок 7;

Крок 4. Видалення кратних дуг і петель.

1. Видалення кратних дуг і петель.

2. Видаляємо всі петлі за таким правилом.

Нехай у вершині qi є петля з відміткоюА. Якщо з цієї вершини немає дуги в іншу вершину, то петля видаляється. В Інакше для всіх дуг (qi, ei, qj), де i≠j, з відміткою дуги В, петля видаляється, а відміткаВ замінюється відміткою А⊛, В ○ В.

На Кроках 5 – 6 відбувається видалення однієї вершини.

Крок 5.

Обираємо qi = Pre(fin);

q := qi; 

Крок 6.

If q ¹ q0 then видаляємо вершинуq і всі вхідні і виходять з неї дуги. Якщо при цьому є довільний шлях з деякої вершини qi у вершину qk, через видаляєму вершину q, де qj належить Pre(q) та qk належить Post(q), то в граф додається дуга, зі & shy; тримає позначку, рівну склеюванню позначок видаляються дуг даного шляху;

goto Крок 2;

else qi рівна q0 не виключается;

обираємо qm =Pre(q0);

q := qm;

goto Крок 6;

Крок 7. Видаляємо всі вершиниq != q0 та q != fin і всі вхідні в них дуги. Отримаємо граф, що складається з двох вершин:q0 таfin і дуги, між ними з позначкоюR, де R – це шукане регулярний вираз.

Нижче приведено алгоритм побудови регулярного виразу по поміченому графу(рис.2).

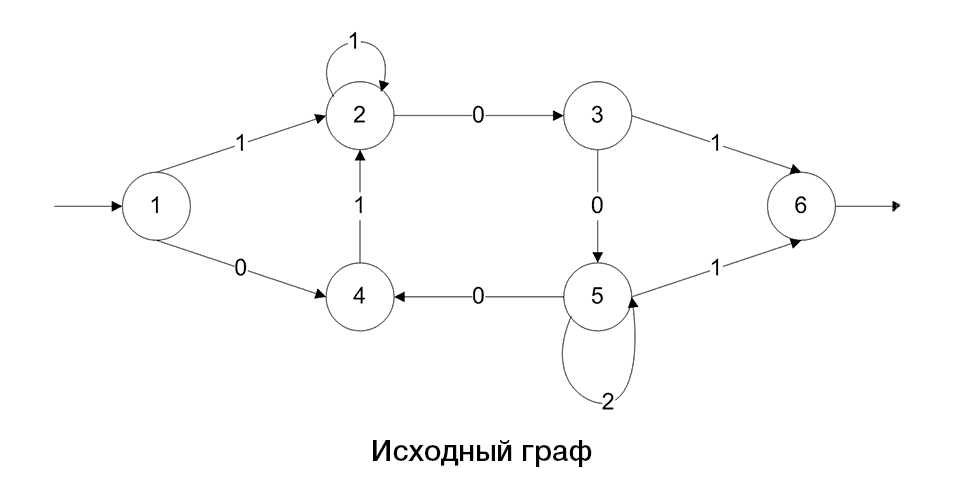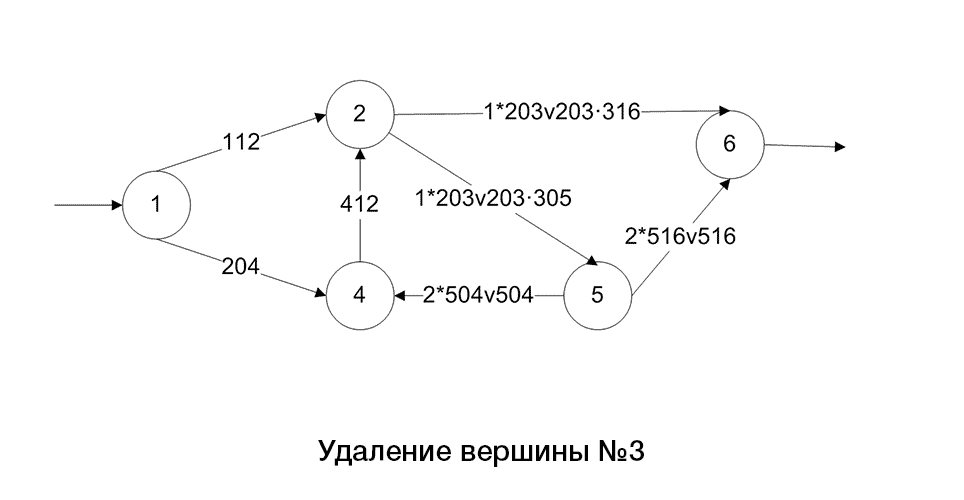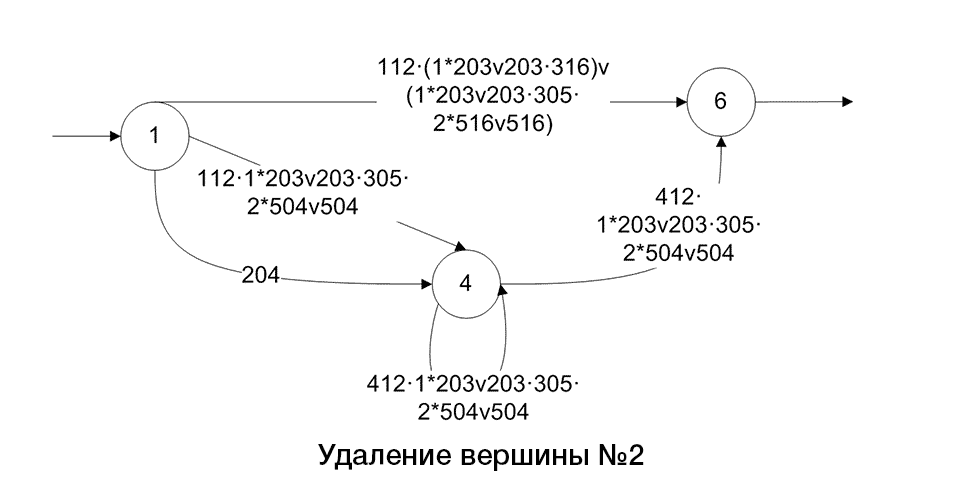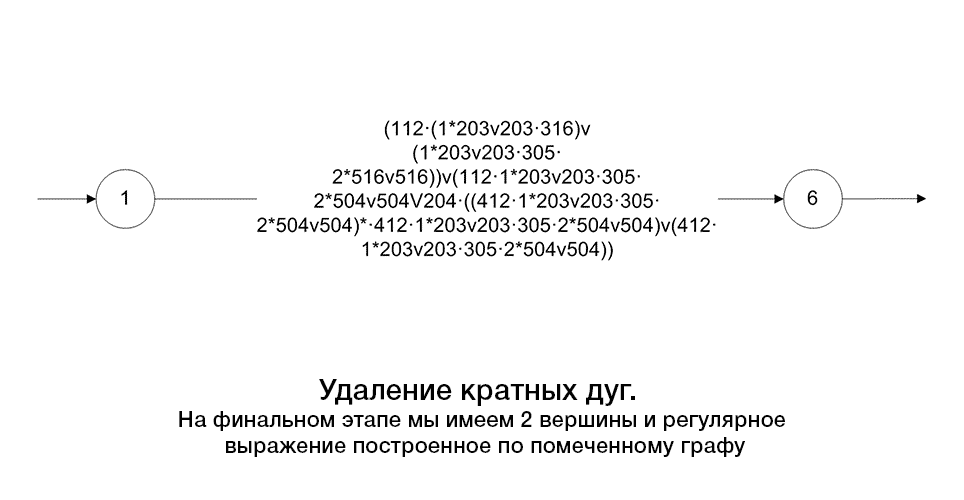
Алгоритм преобразования графа, путем сокращения его дуг и вершин

Рисунок 2 – Алгоритм перетворення графа, шляхом скорочення його дуг і вершин
(анімация: 12 кадрів, 5 циклів повторення, 108 кілобайт)

Види подграфів

На поточному етапі роботи був визначений такий вид графа(рис.3)

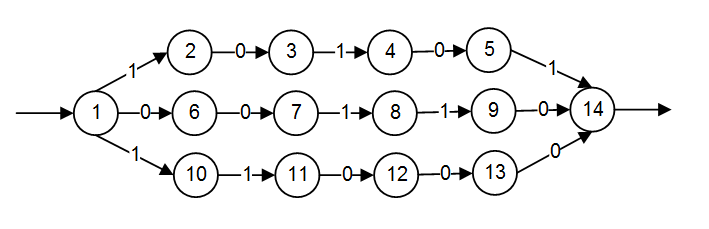
Алгоритм преобразования графа, путем сокращения его дуг и вершин

Рисунок 3 – K-вырожденный ациклический граф двухполюсник

Пояснення: K-вироджений ациклический граф двухполюсник

K-вироджений - у графі є k паралельних шляхів

ациклический - у графі відсутні цикли

двухполюсник - має 1 початкову та 1 кінцеву вершину

Пропонується розробити метод аналізу графів з метою виділення таких подграфов, оскільки для них очевидний простий алгоритм побудови регулярного виразу. Так, для цього графа регулярний вираз = 10101v00110 v11000

Висновки

Оптимізація алгоритму побудови регулярного виразу по позначеному графу є актуальною на сьогоднішній день.

У даній магістерській роботі будуть досліджуватися різні види подграфов, а також оптимальні шляхи їх скорочення. В рамках проведених досліджень виконано:

1. Проаналізовано алгоритм запропонований Ногіною Н.В..

2. На підставі вищевказаного алгоритму були здійснені ручні прорахунки на різних видах графів.

При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2015 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати

Перелік посилань

  1. Ногина Н.В., Грунский И.С. - Синтез регулярного выражения языка,порожденного помеченным графом,методом его локальной редукции, 2012.
  2. Хопкрофт Д. Введение в теорию автоматов, языков и вычислений / Д. Хопкрофт, Р. Мотвани, Д. Ульман. – М.: Издательский дом «Вильямс», 2002. – 528 с.
  3. Кристофидес, Н. Теория графов: алгоритмический подход / Н. Кристофидес. – М.: Мир, 1978. – 430 с.
  4. Ахо А. Построение и анализ вычислительных алгоритмов / А. Ахо, Дж. Хопкрофт, Дж. Ульман. – М.: Мир, 1979. – 536 с.
  5. Батищев Д.И. Многоуровневая декомпозиция гиперграфовых структур / Батищев Д.И., Старостин Н.В., Филимонов А.В. // Прилож. к журналу «Информационные технологии» №5(141). – М.: Новые технологии. – 2008. – 32 с.
  6. Ногина Н.В. Построение кратчайшего пути в помеченном графе при помощи локальной редукции графа / Н.В. Ногина, А.В. Билык // Сучасна інформаційна Україна: інформатика, економіка, філософія: матеріали доповідей конференції, 26 квітня 2012 року. – Донецьк, 2012. – 316 с. – С. 76-79.
  7. Бєлов В.Теорія графів / Бєлов В.– М. : Питер,1968. – 304 с.
  8. Полат Е.С. Новые педагогические и информационные технологии / Полат Е.С. – М. : Akademia, 1999. – 401с.
  9. Кузнєцов О.П. Дискретная математика для инженера / Кузнєцов О.П. – М. : Энергоатомиздат, 1988. – 703 с.
  10. Оре О. Теорія графів / Оре О. – М. : Наука, 1980. – 340 с.
  11. Смольяков Е.Р. Введение в теоpию гpафов / Смоляков Е.Р. – М. : МГТУ, 1992. – 705 с.
  12. Hечепуpенко М.И. Алгоpитмы и пpогpаммы pешения задач на гpафах и сетях / Hечепуpенко И.М. – М. : Hаука, 1990. – 202 с.
  13. Романовский И.В. Алгоpитмы pешения экстpемальных задач / Романовский И.В. – М. : Hаука, 1977. – 506 с.
  14. Землянухин В.Н. Задачи оптимизации на графах / В.Н. Землянухин, Л.Н. Землянухина. – М. : Наука, 2009. – 677 с.
  15. Евстигнеев В.А. Графы в программировании: обработка, визуализация и применение / В.А. Евстигнеев, В.Н. Касьянов. – М. : Наука, 1999. – 266 с.
  16. Новиков Ф.А. Дискретная математика / Новиков Ф.А. – М. : Питер, 2001. – 301 с.
  17. Алгоритмы на графах [Электронный ресурс] - http://www.chasolimp.de/alggraph_prac.htm>