Abstract
At the time of this writing, the master's thesis has not been completed. The planned completion date is summer of 2021.
Table of contents
- Introduction
- 1. Urgency
- 2. The purpose and objectives of the research, the expected results
- 3. Research and development overview
- 3.1. Review of international sources
- 3.2. Review of national sources
- 3.3. Review of local sources
- 4. Introduction to the FEM theory
- Conclusion
- References
Introduction
To analyze the strength characteristics of structures, engineering calculations are carried out using analytical and numerical methods. Analytical methods require a high level of mathematical training from an engineer and, as a rule, allow to solve problems only for bodies with a relatively simple geometric shape. At the same time, the effectiveness of numerical methods is not limited either by complexity of bodies geometry, or by methods of applying forces.
Finite Element Method (FEM) — is one of the modern methods of numerical analysis, which initially developed in two directions independently — in engineering and mathematics. Complex engineering structures were replaced by simpler ones using rods in accordance with the methods of statics of linear supports. In mathematics, the emphasis was on solving boundary value problems, which then implied a variational method. Later, the two approaches merged into one, which was of great importance for the spread of FEM. In 1941 A. P. Hrennikov —, Canadian engineer of Russian origin, — for the first time applied the method of physical discretization of a continuous medium when solving a plane problem of elasticity theory. This prompted other researchers to further explore the properties of discrete structures.
For the first time, the FEM was used to carry out calculations of engineering structures in the 50s of XX c., when the objective was to solve the problem of plane stress. Soon thereafter, FEM became an independent field of science. Its development took place in parallel with the development of computer technology, which also contributed to the expansion of opportunities for research and modeling problems in mathematics, physics and mechanics.
The rapid development of engineering required more accurate calculations, especially in aviation, where high payload and reliability are required with a minimum weight [1][2].
1. Urgency
Reliability and efficiency of a created engineering structures largely depend on the ability to predict their behavior under influence of various external factors. Reliability of prediction, in turn, directly correlates with accuracy of a technologies used for this. Confidence that a new design will withstand an expected loads, while allowing more rational use of materials, introduces some additional functionality or something else, favorably affects the development of a huge number of industries.
One of the most common methods of predicting the behavior of bodies under the influence of external factors today is the finite element method. It is used to solve such problems as the solid mechanics problem, problems of the theory of elasticity, problems of heat propagation, problems of fluid dynamics, etc. Many scientific works and literature are devoted to the theory and implementation of FEM. In addition to its versatility, its popularity is due to its direct connection with the classical methods of structural mechanics and independence from a geometric shape of investigated bodies.
There are many modern structural design tools, where FEM plays one of the most important roles, for example, CAD Catia, SolidWorks, KOMPAS-3D, etc.
2. The purpose and objectives of the study, the expected results
Purpose of study: search for possible ways to optimize the software implementation of the finite element method.
Object of study: finite element method.
Subject of study: optimization of the finite element method algorithm using modern technologies.
The main objectives of study:
- An introduction to the mathematics of FEM.
- FEM software implementation design.
- Analysis of the FEM algorithm for potential optimization areas.
- Analysis of modern methods and technologies capable of optimizing operations in the identified areas.
- Software implementation of the prototype of the optimized FEM algorithm.
Within the master's work, it is expected to obtain the following scientific results:
- List of potential areas for optimization of the FEM algorithm.
- Working prototype of the optimized FEM algorithm.
3. Research and development overview
In the literature on this topic, it is believed that the finite element method is the application of methods of structural mechanics to approximate the solution of problems in continuum mechanics.
Figure 1 shows that the peak period of publications on FEM is the 1980s both for the Russian-speaking and for the English-speaking society.
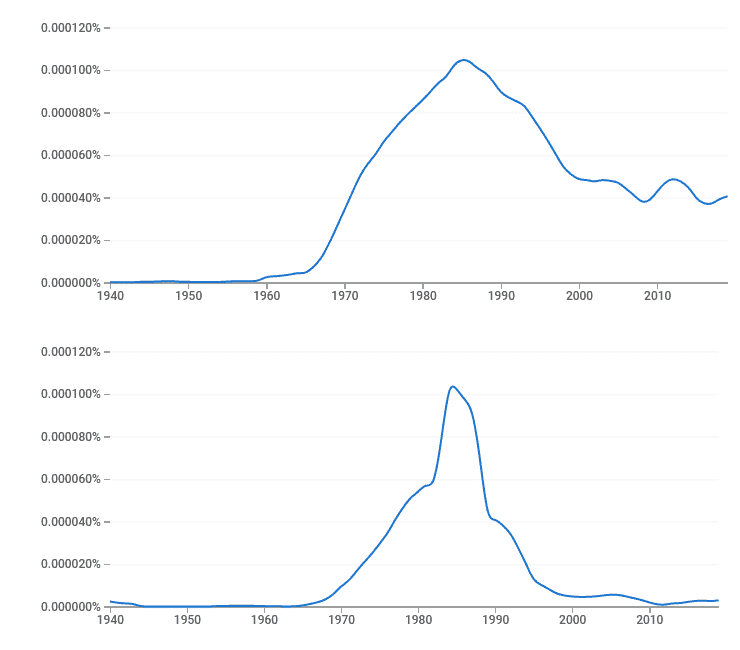
Figure 1. Frequency distribution graphs of FEM mention in literature in English (above) and Russian (below) languages in the period 1940–2019 [3][4]
3.1. Review of international sources
Canadian engineer of Russian origin Alexander Hrennikov and American mathematician of German origin Richard Courant are considered to be one of the founders of ideas underlying the FEM. Their work has been published in the 1940s [5][6]. In his later work, Hrennikov writes that one of the first similarities of the FEM was developed back in 1941 to solve problems of the theory of elasticity by methods of calculating rod systems and was originally used to calculate flat plates, replaced by a mesh system of a large number of connected triangular or rectangular cells.
A significant contribution to the development of FEM was made by Greek John Argyris, who was teaching aviation engineering in London at that time. He was the first to give a general matrix formulation for the calculation of rod systems based on fundamental energy principles, defined the compliance matrix, and later — the stiffness matrix (as the inverse of the compliance matrix). The works of Argyris and his collaborators, published in the period 1954–1960, are the starting point for the matrix formulation of known numerical methods and computer-assisted structural calculations. In his work Energy Theorems and Structural Analysis
, the term finite element
is first encountered. It also summarizes the basic energy principles that were used to calculate structures [7].
American scientist Ray William Clough, in his work The Finite Element Method in Plane Stress Analysis
, when solving the two-dimensional problem of elasticity theory, splits the two-dimensional continuum into triangular or quadrangular elements, which are then connected at nodes. It uses the already well-known matrix formulation, borrows the idea of representing a continuous medium in the form of a finite number of elements. The novelty lies in the fact that two-dimensional and three-dimensional structural elements were used as finite elements [8].
In 2016 M. Nepley achieved performance improvements when integrating FEM using GPUs. At that time, the NVIDIA GTX580 graphics card processed the Laplace operator in the algorithm at a speed of almost 3*10^11 floating point operations per second with variable coefficients in two dimensions and over 4*10^11 — in three, which is dedicated to work Finite Element Integration with Quadrature on the GPU
[9].
In the article A computational framework for G/XFEM material nonlinear analysis
(2017) A. Monteiro et al. describes the developed framework for nonlinear analysis of substances, created to overcome some limitations of FEM [10]. Later M. Malekan with members of the same team published the article Two-dimensional fracture modeling with the generalized/extended finite element method: An object-oriented programming approach
, where he presented an object-oriented oriented G/XFEM implementation [11].
GPU-warp based finite element matrices generation and assembly using coloring method
(2019) by W. Kieran describes new matrix generation strategies for FEM based on the coloring method, and also explains the benefits of CUDA technologies [12].
3.2. Review of national sources
In the book Метод конечных элементов в механике разрушения
(1980) E. Morozov expounds the basic concepts of the finite element method and methods of its implementation in problems of fracture mechanics. The author reveals a wide range of issues — from methods for calculating stress intensity factors in plane and axisymmetric bodies under mechanical and thermal loading of plastically deformed regions and local fracture parameters in the case of a developed plastic zone to a number of computational experiments that help to solve complex problems of mechanical behavior of elastic-plastic bodies with cracks. Appendix to the book contains algorithms for solving basic problems, designed in the form of computer programs in the FORTRAN language [13].
In the Пластическая деформация легких и специальных сплавов
(1982) N. Koryagin examines theoretical and practical issues of the effect of forces on metals and alloys. Methods for studying deformed bodies in a state of stress and heat transfer are disclosed. Conditions and principles of formation of mechanical properties of bodies during hot rolling are stated. The book contains results of studies of plastic deformations of light and special alloys during various interactions of bodies. The issues of resistance to plastic deformation, mechanical properties of bodies during plastic deformation, methods of studying mechanical properties are also considered [14].
In 2004 R. Dautov outlined the main methods of constructing and analyzing FEM circuits in the tutorial Введение в теорию метода конечных элементов
, and in 2014 described their software implementation in the edition Программная реализация метода конечных элементов в МATLAB
[15][16].
In the book Метод конечных элементов. Теория и задачи
(2008) S. Trushin introduces the finite element method in the context of solving applied problems. The algorithm is also described in general form. The issues of static analysis of structures, stability of the deformed state of systems, heat transfer, dynamics and mechanics of fluid are considered. Existing methods for solving nonlinear problems are described [17].
The A. Alamovsky's book COSMOSWorks. Основы расчета конструкций в среде SolidWorks
(2010) mostly talks about the use of the finite element method in a computer-aided design systems, namely, the COSMOSWorks package integrated into the SolidWorks CAD system. The author described the capabilities of the system in the problems of engineering calculation of strength, highlighted the range of tasks solved by this tool. Attention is focused on the mechanics problems. The main issues of finite element modeling are considered: thin-walled structures, joints, contact problem, thermoelasticity and thermal calculation. As examples, both calculations of canonical objects and real production projects are given. Tips are given for the effective operation of the software package for solving problems of fluid dynamics and heat transfer [18].
3.3. Review of local sources
Given the role of the Donetsk National Technical University in the development of the mining industry, it is inextricably linked with the finite element method. The library of DonNTU has hundreds of publications in which the concepts of strength analysis
, prediction of structural deformation
, temperature analysis
, etc. are encountered in one way or another.
L. Lesik, N. Datsun and O. Symonenko in the work Демонстрационная модель деформации металла (прокатка)
(1994) describe a training system for students of metallurgical specialties, which includes information about FEM and its application [19].
In 2002 V. Ovsyannikov, V. Overko and P. Zyma published the article Алгоритм построения расчетной модели участка трубопровода при прочностных расчетах в среде ANSYS
, where, using an example, they explained the algorithm for constructing a pipeline model and calculating its state under the influence of loads in the ANSYS finite element analysis software [20].
I. Sakhno, S. Negrei and A. Lyzenko dedicated to the FEM the article Математическое моделирование деформационных процессов в разрушенных горных породах с помощью метода конечных элементов
(2008), which demonstrates the prediction of the behavior of destroyed rocks and bulk solids [21].
A lot of attention is also paid to the finite element method in the graduation works of DonNTU masters. Among them are: Решение двумерных краевых задач параллельным методом конечных элементов
by Khoroshilov А. V. [22], Расчет барьерных целиков возле затопленных выработок
by Klimov А. А. [23], Исследование процесса упруго-пластической деформации непрерывнолитой слябовой заготовки методом конечных элементов
by Skorokhodov D. А. [24].
4. Introduction to the FEM theory
The basic ideas of the FEM can be illustrated using the simplest boundary value problems. Consider a second-order differential equation with boundary conditions of the first kind:
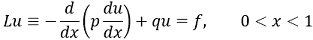 |
(1) |
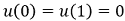 |
(2) |
Let ![C^k[0, 1]](images/formulas/inline/1.png) denote a set of continuous and 𝑘 times continuously differentiable on the interval [0, 1]. By
denote a set of continuous and 𝑘 times continuously differentiable on the interval [0, 1]. By ![C_0^k[0, 1]](images/formulas/inline/2.png) we denote a set of functions that also vanish at the ends of the segment [0, 1]. Let's accept
we denote a set of functions that also vanish at the ends of the segment [0, 1]. Let's accept ![p belongs to C^1[0, 1]](images/formulas/inline/3.png) ,
, ![q and f belong to C[0, 1]](images/formulas/inline/4.png) , moreover
, moreover
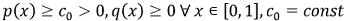 |
(3) |
Let's modify equation (1) by multiplying it by the function ![v belongs to C_0^1[0, 1]](images/formulas/inline/5.png) , and integrate it over the segment [0, 1].
, and integrate it over the segment [0, 1].
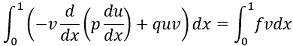 |
(4) |
Applying the formula for integration by parts, we get:
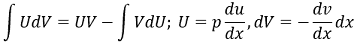 |
(5) |
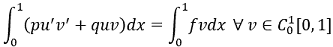 |
(6) |
Relation (6) is an integral identity corresponding to the boundary value problem (1), (2). If 𝑢 satisfies identity (6), then it is a solution to problem (1), (2), and vice versa [15].
For an approximate solution of problem (1), (2), we split the 𝑂𝑋 axis into 𝑛 equal parts of length ℎ, introduce the set of basis functions ![phi belongs to C_0^1[0, 1]](images/formulas/inline/6.png) , which are equal to zero at all x values, except for areas
, which are equal to zero at all x values, except for areas ![[x_(i-1), x]](images/formulas/inline/7.png) , where they grow linearly from 0 to 1, and
, where they grow linearly from 0 to 1, and ![[x, x_(i+1)]](images/formulas/inline/8.png) , where linearly decrease from 1 to 0 (Fig. 2):
, where linearly decrease from 1 to 0 (Fig. 2):
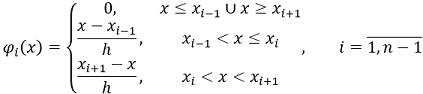 |
(7) |
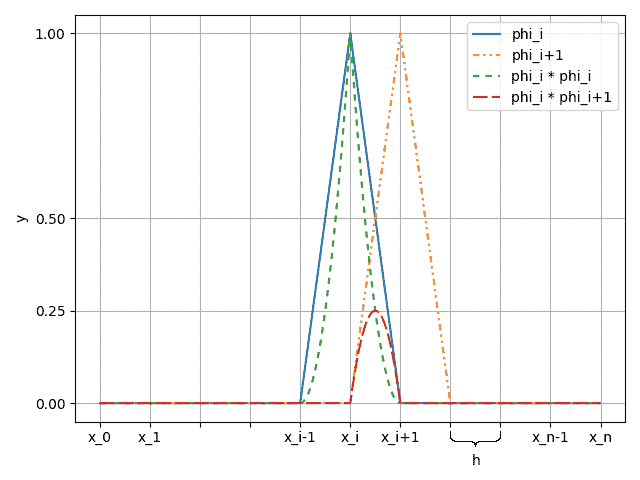
Figure 2. Two adjacent functions 𝜑(𝑥)
The straight line obtained at each segment is a finite element. One of the examples of applied application of this method is predicting the deflection of a stretched string, fixed at two points, under the influence of certain forces.
The required function 𝑢 can be represented as:
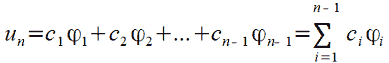 |
(8) |
Then relation (6) can be rewritten as:
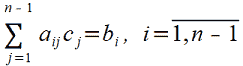 |
(9) |
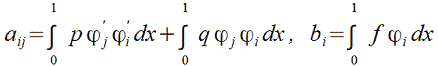 |
(10) |
For simplicity, we define that 𝑝 and 𝑞 are constants and calculate the values of both integrals 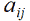 :
:
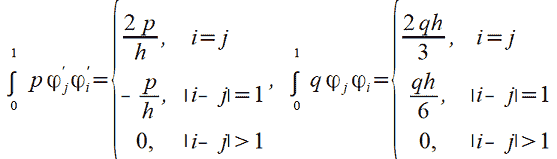 |
(11) |
Thus, we have a system of 𝑛-1 linear equations with 𝑛-1 unknowns, solving which, we obtain the coefficients of the piecewise linear function 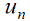 .
.
Conclusion
The finite element method hasn't lost its relevance to this day, occupying an important place in many industries. It is used in solving problems of strength, elasticity, fluid dynamics, heat distribution, etc. Modern CAD systems that are in demand include modules with FEM implementation, which once again confirms its relevance.
In the course of work on the master's thesis, a program has been developed so far that allows you to clearly demonstrate the operation of the FEM in the simplest case — the problem of deflection of a stretched string, fixed at two points, under the influence of certain forces. As input parameters, it takes the functions 𝑝, 𝑞 and 𝑓, boundaries of investigated interval 𝑥𝑙 and 𝑥𝑟, number of partitions of interval 𝑛. The result is coefficients 𝑐 of the piecewise linear function 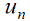 , as well as a forces distribution graph (in accordance with the given function 𝑓) and a graph of expected string deflection.
, as well as a forces distribution graph (in accordance with the given function 𝑓) and a graph of expected string deflection.
The results of the program operation on some sets of input parameters are shown below: the dependence of the approximation accuracy on the number of interval partitions is displayed (Fig. 3) and the dependence of the prediction of the string deflection on the value of the applied force (Fig. 4). The blue solid line illustrates the force distribution, the orange dash-dotted line — predicts the deflection of a string under the influence of this force.
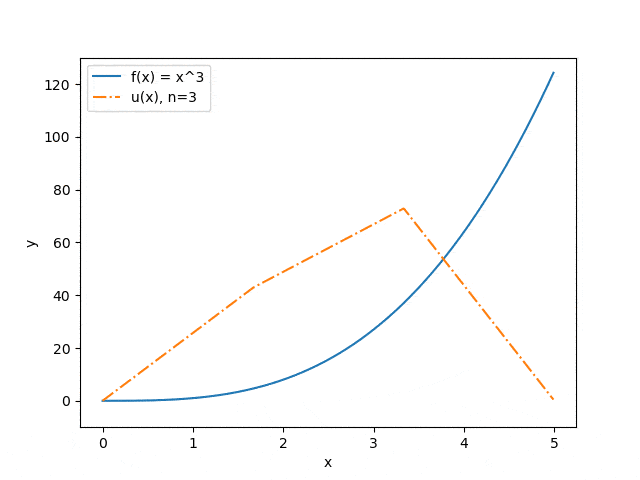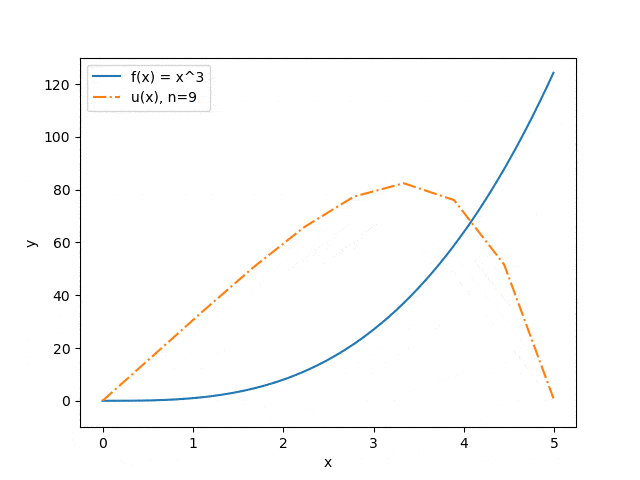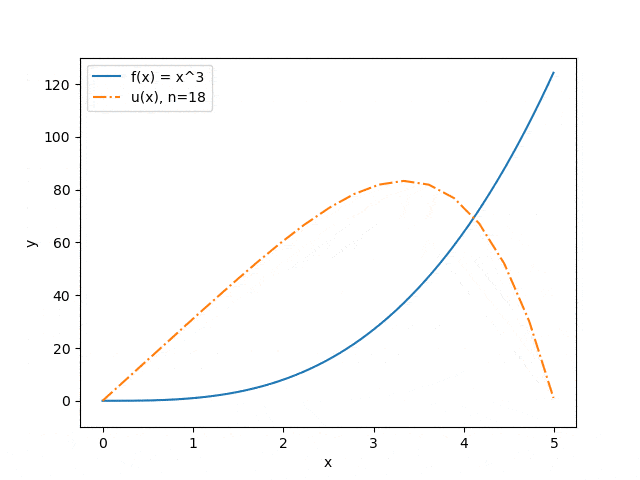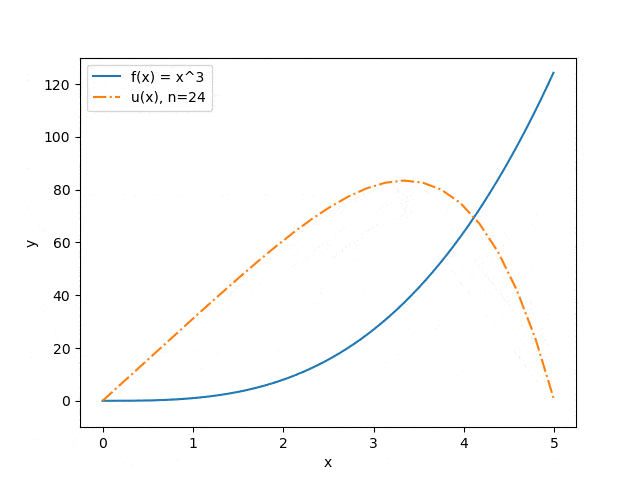
Figure 3. Dependence of the approximation accuracy on the number of interval partitions
(animation: 39.67 Kb, 640x480, 8 frames, frame duration 200 ms, 10 repetition cycles)
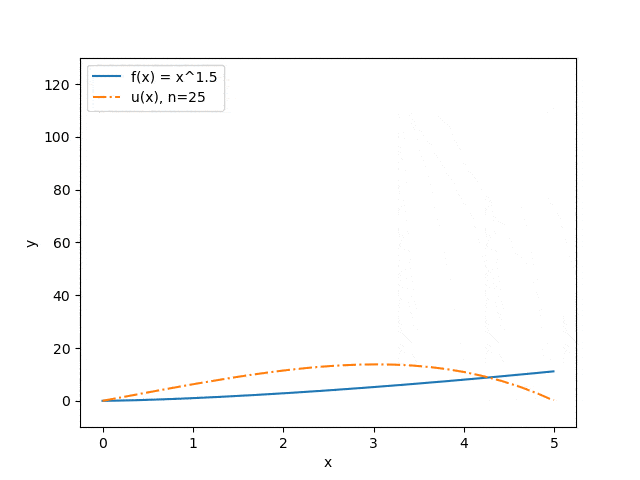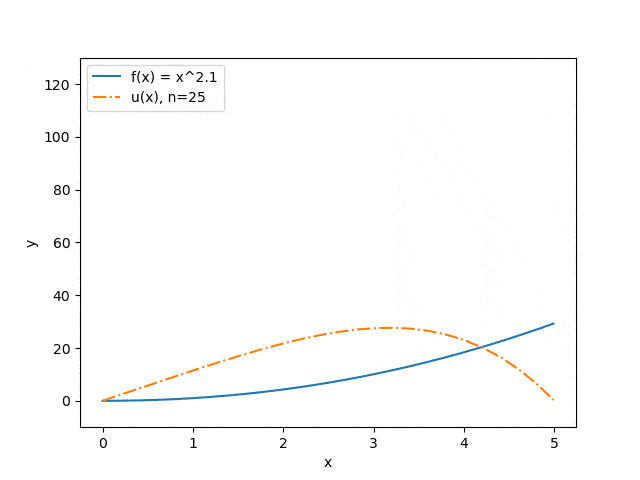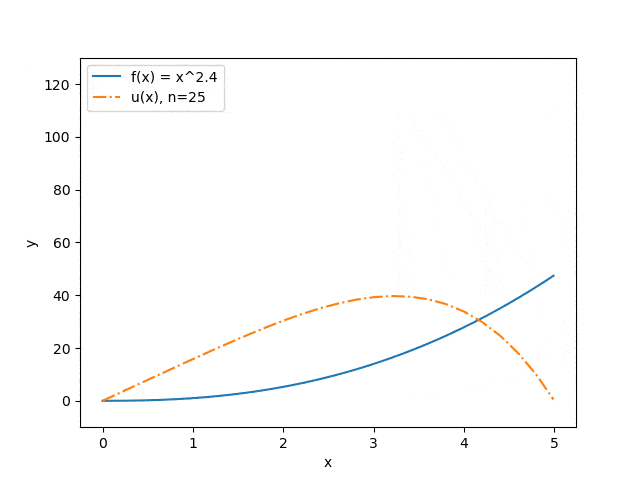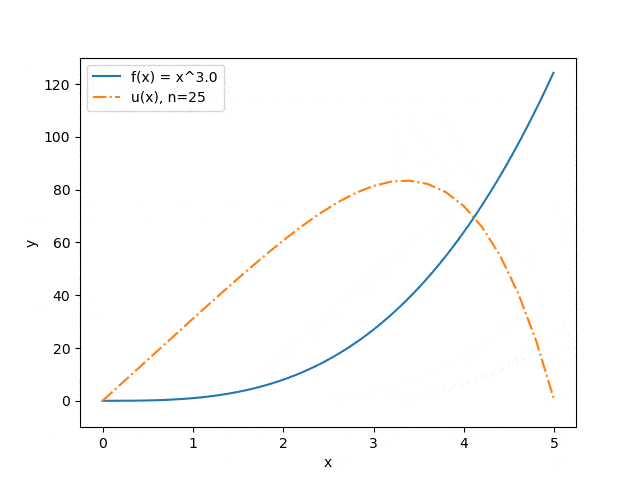
Figure 4. Dependence of the predicted string deflection on the magnitude of the applied force
(animation: 31.43 Kb, 640x480, 6 frames, 400 ms frame duration, 10 repetition cycles)
It has been established that in the process of processing each finite element, the same sequence of operations is performed. This situation, when it is required to execute the same instructions over and over again for a large amount of input data, in other words, SIMD (single instruction, multiple data), is favorable for improving performance using GPUs. Modern models of home central processors have dozens of computing cores on board, while video cards — thousands.
Even in the considered simplest case of the FEM problem, several potential areas for optimization have been identified. Firstly, given that the solution of the problem implies the solution of a SLAE (system of linear algebraic equations), and the number of equations can be huge, in the context of GPGPU (general-purpose computing on graphics processing units), parallelization of the process of coefficients matrix forming obviously suggests itself. Secondly, taking into account the specifics of the FEM, one can be sure that the coefficients matrix will be sparse, namely — tridiagonal. Therefore, it is proposed to abandon the usual representation of matrices in the form of two-dimensional arrays, thereby saving not only the execution time, but also the amount of memory consumed. Thirdly, there is an opportunity to win on the very solution of the SLAE by assigning this subtask to the cuSPARSE library, which contains ready-made optimized algorithms for this purpose [25].
References
- Секулович М. Метод конечных элементов / Пер. с серб. Ю. Н. Зуева; под ред. В. Ш. Барбакадзе. — М.: Стройиздат, 1993 — 664 с.: ил. — Перевод изд. Metid konacnih elemenata / Miodrag Sekulovic, 1988. — ISBN 5-274-01755-X.
- Шимановский А. Применение метода конечных элементов в решении задач прикладной механики : учеб.-метод. по собие для студентов технических специальностей / А. О. Шимановский, А. В. Путято ; М-во образования Респ. Беларусь, Белорус. гос. ун-т трансп. — Гомель : БелГУТ, 2008. — 61 с. ISBN 978-985-468-474-1.
- Finite element method [Electronic resource] // Google Books Ngram Viewer. URL: https://books.google.com/ngrams/graph?content=f... (accessed 2020 Nov 18).
- Метод конечных элементов [Electronic resource] // Google Books Ngram Viewer. URL: https://books.google.com/ngrams/graph?content=м... (accessed 2020 Nov 18).
- Courant R. Variational methods for the solution of problems of equilibrium and vibrations / R. Courant // Bull. Amer. Math. Soc, 1943. vol 49(1). — pp. 1-23.
- Hrennikoff A. Solution of Problems of Elasticity by the Framework Method / A. Hrennikoff // Journal of Applied Mechanics, 1941. — vol 7(4). — pp. 0-0.
- Argyris J. Energy Theorems and Structural Analysis: A Generalized Discourse with Applications on Energy Principles of Structural Analysis Including the Effects of Temperature and Non‐Linear Stress‐Strain Relations Part I. General Theory / J. H. Argyris // Aircraft Engineering and Aerospace Technology, 1955. — vol 27(3). — pp. 80-94.
- Clough R. The Finite Element Method in Plane Stress Analysis / R. W. Clough. — American Society of Civil Engineers, 1960. — 35 pp.
- Knepley M. Finite Element Integration with Quadrature on the GPU / M. G. Knepley, K. Rupp, A. R. Terrel // CoRR, 2016. — vol. abs/1607.04245. — 14 pp.
- Monteiro A. A computational framework for G/XFEM material nonlinear analysis / A. B. Monteiro, A. R. V. Wolenski, F. B. Barros, R. L. S. Pitangueira, S. S.Penna // Advances in Engineering Software, 2017. — vol. 114. — pp. 380-393.
- Malekan M. Two-dimensional fracture modeling with the generalized/extended finite element method: An object-oriented programming approach / M. Malekan, L. L. Silva, F. B. Barros, R. L. S. Pitangueira, S. S. Penna // Advances in Engineering Software, 2018. — vol. 115. — pp. 168-193.
- Kiran U. GPU-warp based finite element matrices generation and assembly using coloring method / U. Kiran, D. Sharma. S. S. Gautam // Journal of Computational Design and Engineering, 2019. — vol. 6(4). — pp. 705-718.
- Морозов Е. Метод конечных элементов в механике разрушения / Морозов Е. М., Никишков Г. П. — М.: Наука, 1980. — 256 с.
- Корягин Н. Пластическая деформация легких и специальных сплавов / Н. И. Корягин, А. Ф. Белов, А. С. Кузнецов и др. Пластическая деформация легких и специальных сплавов. Часть 2. — Сборник статей. — М.: Металлургия, 1982. — 201 с.
- Р. Даутов. Введение в теорию метода конечных элементов / Р. З. Даутов, М. М. Карчевский. — Учебное пособие. — Казань: КГУ, 2004. — 239 с.
- Р. Даутов. Программная реализация метода конечных элементов в МATLAB / Даутов Р. З. — Казань: КФУ, 2014. — 106 с.
- Трушин С. Метод конечных элементов. Теория и задачи / С. И. Трушин. — М.: АСВ, 2008. — 256 с.
- Алямовский А. COSMOSWorks. Основы расчета конструкций на прочность в среде SolidWorks / А. А. Алямовский. — ДМК Пресс, 2010. — ISBN 5-94074-582-2.
- Лесик Л. Демонстрационная модель деформации металла (прокатка) / Л. Н. Лесик, Н. Н. Дацун, О. А. Симоненко // Комп’ютерні програми учбового призначення: Тез. доп. II Міжнар. конф. (3-7 верес. 1994 р.). - Донецьк: ДонДУ, 1994. — с.115.
- Овсянниов В. Алгоритм построения расчетной модели участка трубопровода при прочностных расчетах в среде ANSYS / В. П. Овсянников, В. М. Оверко, П. Ф. Зима // Наукові праці Донецького національного технічного університету. Серія: гірничо-електромеханічна. Випуск 51. - Донецьк: ДонНТУ, 2002.
- Негрей С. Математическое моделирование деформационных процессов в разрушенных горных породах с помощью метода конечных элементов / С. Г. Негрей, И. Г. Сахно, А. А. Лызенко // Новые технологии подземного строительства и добычи полезных ископаемых: Материалы между-народной научно-технической конференции. - Алчевск: ДонГТУ, 2008.
- Хорошилов А. Решение двумерных краевых задач параллельным методом конечных элементов [Electronic resource] // Портал магистров ДонНТУ. URL: http://masters.donntu.ru/2006/fvti/horoshilov/... (accessed 2020 Nov 11).
- Климов А. Расчет барьерных целиков возле затопленных выработок [Electronic resource] // Портал магистров ДонНТУ. URL: http://masters.donntu.ru/2008/ggeo/klimov/diss... (accessed 2020 Nov 11).
- Скороходов Д. Исследование процесса упруго-пластической деформации непрерывнолитой слябовой заготовки методом конечных элементов [Electronic resource] // Портал магистров ДонНТУ. URL: http://masters.donntu.ru/2013/fmf/scorohodov/d... (accessed 2020 Nov 11).
- cuSPARSE [Electronic resource] // CUDA Toolkit Documentation. URL: https://docs.nvidia.com/cuda/cusparse/index.html (accessed 2020 Oct 06).
