Реферат за темою випускної роботи
На момент написання даного реферату магістерська дисертація не завершена. Планована дата завершення роботи — літо 2021 р.
Содержание
- Вступ
- 1. Актуальність теми
- 2. Мета і задача дослідження, плановані результати
- 3. Огляд досліджень та розробок
- 3.1. Огляд міжнародних джерел
- 3.2. Огляд національних джерел
- 3.3. Огляд локальних джерел
- 4. Введення в теорію МСЕ
- Висновки
- Список джерел
Вступ
Для аналізу міцності конструкцій проводять інженерні розрахунки із застосуванням аналітичних і чисельних методів. Аналітичні методи вимагають від інженера високого рівня математичної підготовки і, як правило, дозволяють вирішувати задачі тільки для тіл з відносно простою геометричною формою. Ефективність чисельних методів в той же час не обмежується ані складністю геометрії тіл, ані способами докладання зусиль.
Метод скінченних елементів (МСЕ) — один із сучасних методів чисельного аналізу, який спочатку розвивався в двох напрямках незалежно — в інженерній справі і в математиці. Складні інженерні конструкції замінювалися простими з використанням стержнів згідно з методами статики лінійних опор. В математиці акцент був на вирішенні крайових задач, які тоді мали на увазі варіаційний метод. Пізніше два підходи злилися в один, що мало велике значення для поширення МСЕ. У 1941 р. А. П. Хренніков — канадський інженер російського походження — вперше застосував метод фізичної дискретизації суцільного середовища при вирішенні плоскої задачі теорії пружності. Це підштовхнуло інших дослідників до подальшого вивчення властивостей дискретних структур.
Вперше МСЕ був застосований для проведення розрахунків інженерних конструкцій у 50-х рр. ХХ ст., коли задачею було вирішення проблеми плоскої напруги. Незабаром після цього МСЕ став самостійною галуззю науки. Його розвиток відбувався паралельно із розвитком комп'ютерної обчислювальної техніки, що також сприяло розширенню можливостей для дослідження і моделювання задач математики, фізики і механіки.
Швидкий розвиток інженерної думки вимагав більш точних розрахунків, особливо в авіації, де потребуються високі показники вантажопідйомності і надійності при мінімальній масі [1][2].
1. Актуальність теми
Надійність і ефективність створюваних інженерних конструкцій в великій мірі залежать від можливості прогнозування їх поведінки під впливом різних зовнішніх факторів. Достовірність прогнозування в свою чергу безпосередньо корелює з точністю застосовуваних для цього технологій. Впевненість у тому, що нова конструкція витримає передбачувані навантаження, та при цьому дозволяє більш раціонально витрачати матеріали, привносить якісь додаткові функціональні можливості або ще що-небудь, сприятливо позначається на розвитку величезної кількості галузей промисловості.
Одним з найбільш поширених методів прогнозування поведінки тіл під впливом зовнішніх факторів сьогодні є метод скінченних елементів. З його допомогою вирішуються такі задачі, як задача механіки деформації твердого тіла, задачі теорії пружності, задачі про поширення тепла, задачі гідрогазодинаміки та ін. Теорії та реалізації МСЕ присвячено безліч наукових робіт та літератури. Крім універсальності, його популярність обумовлена безпосереднім зв'язком з класичними методами будівельної механіки та незалежністю від геометричної форми досліджуваних тіл.
Існує безліч сучасних інструментів проектування конструкцій, де МСЕ відіграє одну з найважливіших ролей, наприклад, САПР Catia, SolidWorks, КОМПАС-3D та ін.
2. Мета і завдання дослідження, плановані результати
Мета дослідження: пошук можливих шляхів оптимізації програмної реалізації методу скінченних елементів.
Об'єкт дослідження: метод скінченних елементів.
Предмет дослідження: оптимізація алгоритму методу скінченних елементів із застосуванням сучасних технологій.
Основні завдання дослідження:
- Ознайомлення з математикою МСЕ.
- Проектування програмної реалізації МСЕ.
- Аналіз алгоритму МСЕ на предмет потенційних ділянок оптимізації.
- Аналіз сучасних методів і технологій, здатних оптимізувати операції у виявлених ділянках.
- Програмна реалізація прототипу оптимізованого алгоритму МСЕ.
В рамках магістерської роботи планується отримання наступних наукових результатів:
- Список потенційних ділянок оптимізації алгоритму МСЕ.
- Робочий прототип оптимізованого алгоритму МСЕ.
3. Огляд досліджень та розробок
В літературі по даній темі вважається, що метод скінченних елементів полягає в застосуванні методів будівельної механіки для апроксимації рішення задач механіки суцільних середовищ.
На малюнку 1 видно, що піковим періодом публікацій на тему МСЕ є 1980-ті рр. як для російськомовного, так і для англомовного суспільства.
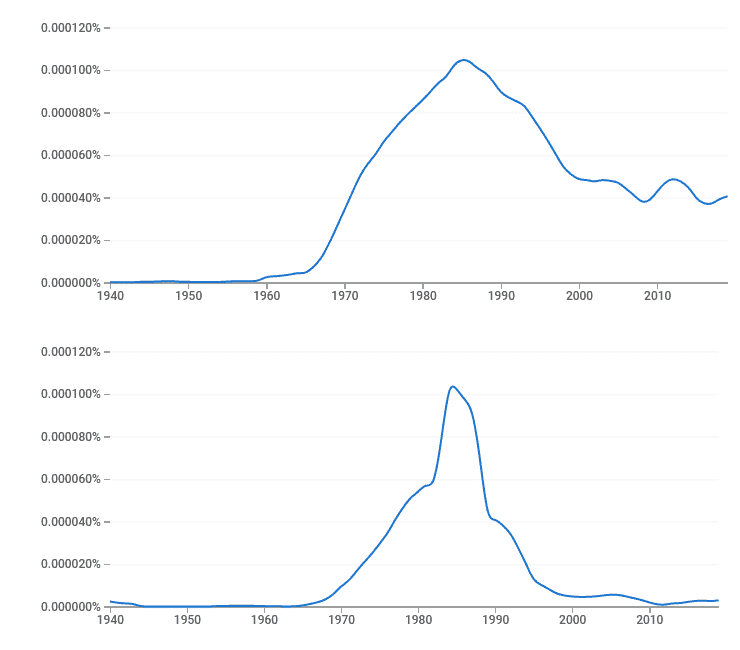
Малюнок 1 — Графіки розподілу частоти згадки МСЕ в літературі англійською (зверху) та російською (знизу) мовами в період 1940–2019 рр. [3][4]
3.1. Огляд міжнародних джерел
Одними з основоположників ідей, що лежать у початків МСЕ, вважаються канадський інженер російського походження Олександр Хренніков та американський математик німецького походження Ріхард Курант. Їх роботи опубліковані в 1940-х роках [5][6]. У своїй пізнішій роботі Хренніков пише, що один з перших подоб МСЕ був розроблений ще у 1941 р. для вирішення проблем теорії пружності методами розрахунків стрижневих систем і спочатку застосовувався для розрахунку плоских плит, замінних сітчастою системою з великої кількості з'єднаних трикутних або прямокутних осередкі.
Значний внесок у розробку МСЕ зробив грек Іоанніс Аргіріс, який викладав в той час авіаінженерію в Лондоні. Він вперше дав загальне матричне формулювання розрахунку стрижневих систем на базі фундаментальних енергетичних принципів, визначив матрицю податливості, а пізніше — матрицю жорсткості (як зворотню матриці податливості). Роботи Аргіріса і його співробітників, опубліковані в період 1954—1960 рр., є стартовою точкою для матричнго формулювання відомих чисельних методів та розрахунків конструкцій із застосуванням ЕОМ. У його роботі Energy Theorems and Structural Analysis
вперше зустрічається термін скінченний елемент
. У ній ж здійснено узагальнення основних енергетичних принципів, які використовувалися для розрахунку конструкцій [7].
Американський вчений Рей Вільям Клаф у своїй роботі The Finite Element Method in Plane Stress Analysis
при вирішенні двовимірної задачі теорії пружності дробить двовимірний континуум на трикутні або чотирикутні елементи, які після з'єднуються у вузлах. У ній використане вже відоме матричне формулювання, запозичена ідея вистави суцільного середовища у вигляді скінченного числа елементів. Новизна полягає в тому, що в якості скінченних елементів використовувалися двовимірні і тривимірні конструктивні елементи [8].
У 2016 р. М. Неплі домігся підвищення продуктивності при інтегруванні МСЕ з використанням графічних процесорів. На той момент відеокарта NVIDIA GTX580 обробляла в алгоритмі оператор Лапласа зі швидкістю майже 3*10^11 операцій з плаваючою комою на секунду зі змінними коефіцієнтами у двох вимірах і понад 4*10^11 — у трьох, чому присвячена робота Finite Element Integration with Quadrature on the GPU
[9].
У статті A computational framework for G/XFEM material nonlinear analysis
(2017 р.) А. Монтейро зі співавторами описує розроблений фреймворк для нелінійного аналізу речовин, створений з метою подолання деяких обмежень МСЕ [10]. Пізніше М. Малекан з учасниками тієї ж команди опублікував статтю Two-dimensional fracture modeling with the generalized/extended finite element method: An object-oriented programming approach
, де представив об'єктно-орієнтовану реалізацію G/XFEM [11].
Робота GPU-warp based finite element matrices generation and assembly using coloring method
(2019 р.) під авторством У. Кірана описує нові стратегії генерації матриць для МСЕ на основі методу розмальовки, а також пояснює витягнуту користь технологій CUDA [12].
3.2. Огляд національних джерел
У книзі Метод конечных элементов в механике разрушения
(1980 р.) Є. Морозов викладає основні поняття методу скінченних елементів та способи його реалізації в задачах механіки руйнування. Автор розкриває широке коло питань — від методів розрахунку коефіцієнтів інтенсивності напружень в плоских та осесиметричних тілах при механічному і термічному навантаженні пластично деформованих областей і параметрів локального руйнування в разі розвиненої пластичної зони до ряду обчислювальних експериментів, які допомагають вирішенню складних питань механічної поведінки пружно-пластичних тіл з тріщинами. У додатку до книзі дані алгоритми вирішення основних завдань, оформлених у вигляді програм для ЕОМ на мові ФОРТРАН [13].
У Пластической деформации легких и специальных сплавов
(1982 р.) Н. Корягін розглядає теоретичні та практичні питання впливу сил на метали та сплави. Розкрито методи дослідження деформованих тіл в стані напруги та теплообміну. Викладено умови та принципи формування механічних властивостей тел під час гарячої прокатки. Книга містить результати досліджень пластичних деформацій легких та спеціальних сплавів при різних взаємодіях тіл. Також розглянуті питання опору пластичної деформації, механічних властивостей тіл при пластичної деформації, методики дослідження механічних властивостей [14].
У 2004 р. Р. Даутов виклав основні способи побудови і аналізу схем МСЕ в навчальному посібнику Введение в теорию метода конечных элементов
, а у 2014 р. описав їх програмну реалізацію у виданні Программная реализация метода конечных элементов в МATLAB
[15][16].
У книзі Метод конечных элементов. Теория и задачи
(2008 р.) С. Трушин знайомить з методом скінченних елементів в контексті вирішення прикладних завдань. Описано також і алгоритм в загальній формі. Розглядаються питання статичного розрахунку конструкцій, стійкості деформованого стану систем, теплопередачі, динаміки і механіки рідини. Описано існуючі методи рішення нелінійних задач [17].
Книга А. Алямовського COSMOSWorks. Основы расчета конструкций в среде SolidWorks
(2010 р.) більшою мірою розповідає про використання методу скінченних елементів в системах автоматизованого проектування, а саме про пакет COSMOSWorks, інтегрований у CAD-систему SolidWorks. Автор описав можливості системи в задачах інженерного розрахунку міцності, виділив коло розв'язуваних цим інструментом завдань. Увага акцентується на проблемах галузі механіки. Розглянуто основні питання скінченно-елементного моделювання: тонкостінні конструкції, з'єднання, контактна задача, Термопружність і тепловий розрахунок. Для прикладу наведено як розрахунки канонічних об'єктів, так і реальних виробничих проектів. Дано поради щодо ефективної експлуатації програмного пакета для вирішення задач гідрогазодинаміки та теплопередачі [18].
3.3. Огляд локальних джерел
Враховуючи роль Донецького національного технічного університету в розвитку гірничої промисловості, він нерозривно пов'язаний з методом скінченних елементів. Бібліотека ДонНТУ налічує сотні публікацій, в яких в тому чи іншому ключі зустрічаються поняття розрахунок на міцність
, прогнозування деформації споруд
, температурний аналіз
та ін.
Л. Лесик, Н. Дацун та О. Симоненко у роботі Демонстрационная модель деформации металла (прокатка)
(1994 р.) описують навчальну систему для студентів металургійних спеціальностей, яка в т. ч. містить відомості про МСЕ та його застосування [19].
В 2002 году В. Овсянников, В. Оверко и П. Зима опублікували статтю Алгоритм построения расчетной модели участка трубопровода при прочностных расчетах в среде ANSYS
, де на прикладі пояснили алгоритм побудови моделі трубопроводу і розрахунку його стану під впливом навантажень в програмній системі скінченно-елементного аналізу ANSYS [20].
И. Сахно, С. Негрей и А. Лизенко присвятили МСЕ статтю Математическое моделирование деформационных процессов в разрушенных горных породах с помощью метода конечных элементов
(2008 р.), в якій демонструється прогнозування поведінки зруйнованих порід та сипучих тіл [21].
Методу скінченних елементів також приділяється чимало уваги і в випускних роботах магістрів ДонНТУ. Серед них: Решение двумерных краевых задач параллельным методом конечных элементов
Хорошилова О. В. [22], Расчет барьерных целиков возле затопленных выработок
Климова О. А. [23], Исследование процесса упруго-пластической деформации непрерывнолитой слябовой заготовки методом конечных элементов
Скороходова Д. А. [24].
4. Введення в теорію МСЕ
Основні ідеї МСЕ можуть бути проілюстровані за допомогою найпростіших крайових задач. Розглянемо диференціальне рівняння другого порядку з крайовими умовами першого роду:
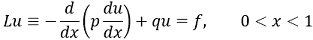 |
(1) |
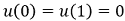 |
(2) |
Через ![C^k[0, 1]](images/formulas/inline/1.png) позначимо множину безперервних та 𝑘 раз безперервно диференційовних на відрізку [0, 1]. Через
позначимо множину безперервних та 𝑘 раз безперервно диференційовних на відрізку [0, 1]. Через ![C_0^k[0, 1]](images/formulas/inline/2.png) — множину функцій, які також звертаються в нуль на кінцях відрізку [0, 1]. Приймемо
— множину функцій, які також звертаються в нуль на кінцях відрізку [0, 1]. Приймемо ![p належить C^1[0, 1]](images/formulas/inline/3.png) ,
, ![q и f належить C[0, 1]](images/formulas/inline/4.png) , причому
, причому
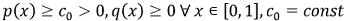 |
(3) |
Видозмінимо рівняння (1), помноживши його на функцію ![v належить C_0^1[0, 1]](images/formulas/inline/5.png) , та проінтегруємо його по відрізку [0, 1].
, та проінтегруємо його по відрізку [0, 1].
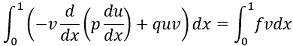 |
(4) |
Застосувавши формулу інтегрування частинами, отримаємо:
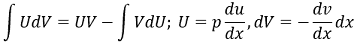 |
(5) |
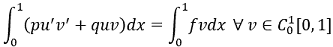 |
(6) |
Співвідношення (6) є інтегральною тотожністю, відповідною крайовій задачі (1), (2). Якщо 𝑢 задовольняє тотожності (6), то воно є рішення задачі (1), (2), і навпаки [15].
Для наближеного розв'язання задачі (1), (2) розіб'ємо вісь 𝑂𝑋 на 𝑛 рівних частин довжиною ℎ, введемо множину базисних функцій ![phi належить C_0^1[0, 1]](images/formulas/inline/6.png) , які дорівнюють нулю на всіх значеннях іксу, крім областей
, які дорівнюють нулю на всіх значеннях іксу, крім областей ![[x_(i-1), x]](images/formulas/inline/7.png) , де вони лінійно зростають від 0 до 1, и
, де вони лінійно зростають від 0 до 1, и ![[x, x_(i+1)]](images/formulas/inline/8.png) , де лінійно зменшуються від 1 до 0 (див. мал. 2):
, де лінійно зменшуються від 1 до 0 (див. мал. 2):
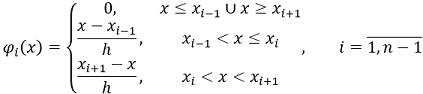 |
(7) |
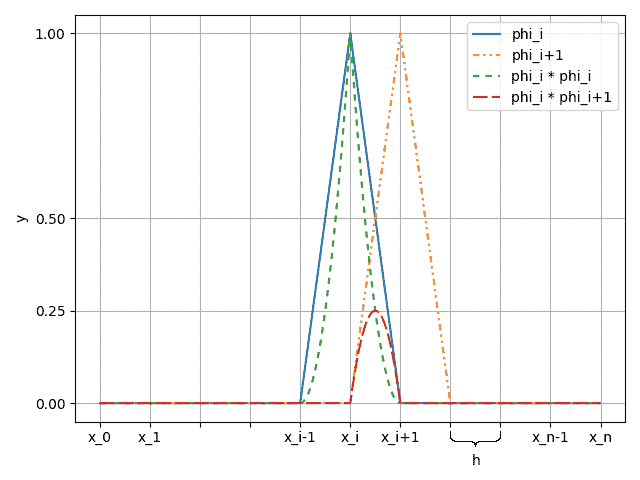
Малюнок 2 — Дві сусідні функції 𝜑(𝑥)
Пряма лінія, отримана на кожному відрізку, є скінченний елемент. Один із прикладів прикладного застосування цього методу — передбачення прогину натягнутої струни, закріпленої в двох точках, під впливом певних сил.
Шукану функцію 𝑢 можна зобразити як:
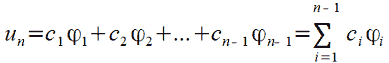 |
(8) |
Тоді співвідношення (6) можна переписати у вигляді:
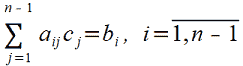 |
(9) |
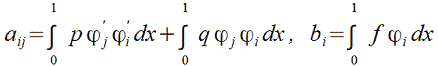 |
(10) |
Для простоти визначимо, що 𝑝 та 𝑞 - константи, й обчислимо значення обох інтегралів 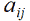 :
:
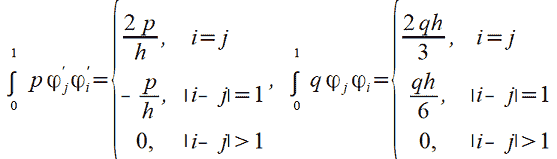 |
(11) |
Таким чином, маємо систему з 𝑛-1 лінійних рівнянь з 𝑛-1 невідомими, вирішивши яку, отримаємо коефіцієнти кусочно-лінійної функції 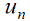 .
.
Висновки
Метод скінченних елементів донині не втрачає актуальності, займаючи важливе місце в багатьох галузях промисловості. Він застосовується в рішенні задач міцності, пружності, гідрогазодинаміки, розподілу тепла та ін. Сучасні системи автоматизованого проектування, що користуються попитом, включають в себе модулі з реалізацією МСЕ, що зайвий раз підтверджує його затребуваність.
В ході роботи над магістерською дисертацією на даний момент створена програма, що дозволяє наочно продемонструвати роботу МСЕ в найпростішому випадку — задачі про прогин натягнутої струни, закріпленої в двох точках, під впливом певних сил. В якості вхідних параметрів вона приймає функції 𝑝, 𝑞 та 𝑓, межі досліджуваного інтервалу 𝑥𝑙 та 𝑥𝑟, кількість розбитів інтервалу 𝑛. Як результат повертаються коефіцієнти 𝑐 кусочно-лінійної функції 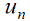 , а також будується графік розподілу сил (відповідно до заданої функцією 𝑓) та передбачуваного прогину струни.
, а також будується графік розподілу сил (відповідно до заданої функцією 𝑓) та передбачуваного прогину струни.
Нижче продемонстровані результати роботи програми на деяких наборах вхідних параметрів: відображена залежність точності наближення від кількості розбитів інтервалу (див. мал. 3) і залежність прогнозу прогину струни від величини прикладеного сили (див. мал. 4). Синя суцільна лінія ілюструє розподіл сили, помаранчевий штрих-пунктир — прогноз прогину струни під впливом цієї сили.
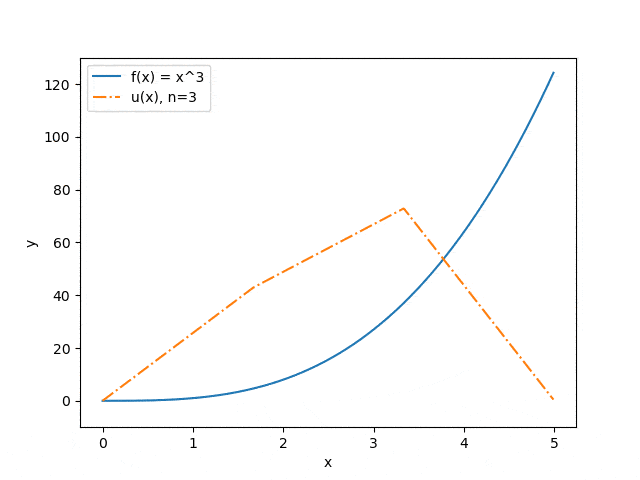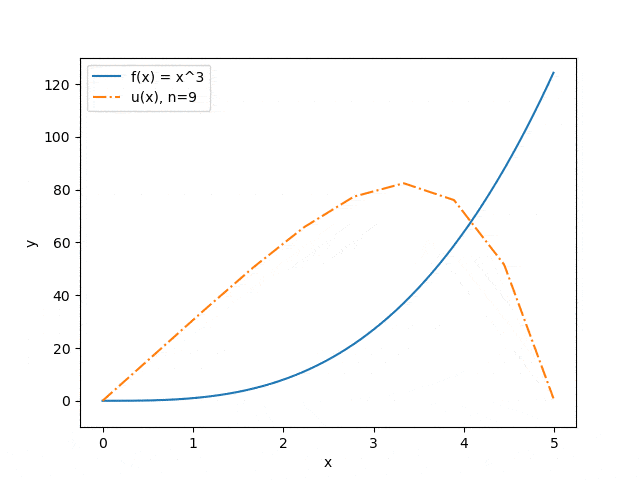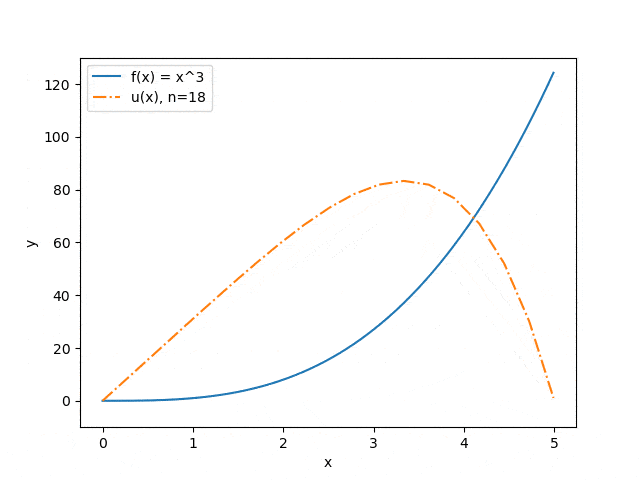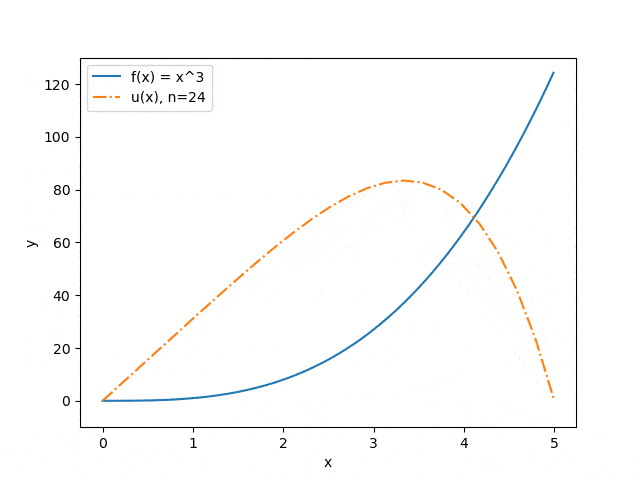
Малюнок 3 — Залежність точності наближення від кількості розбитів інтервалу
(анимація: 39.67 Кб, 640x480, 8 кадрів, тривалість кадру 200 мс, 10 циклів повторення)
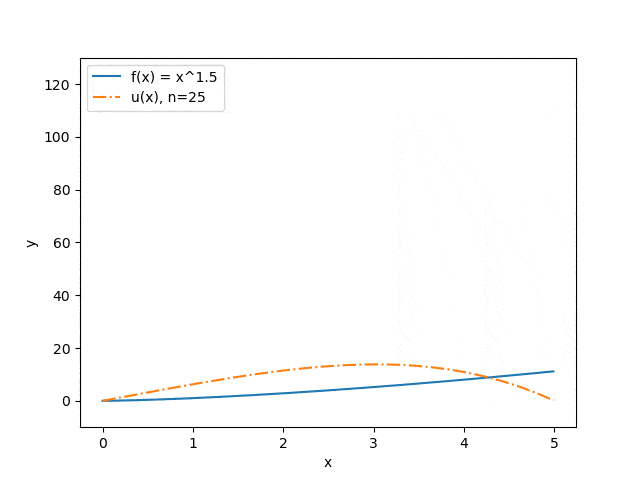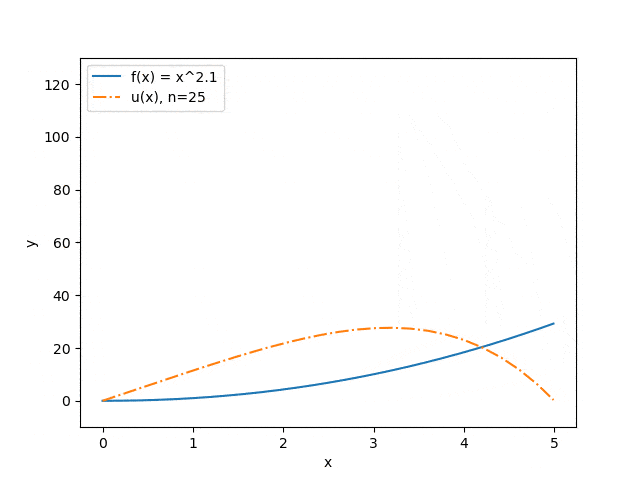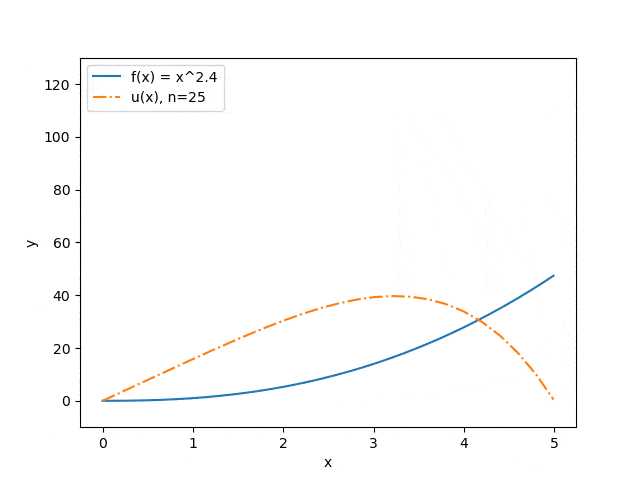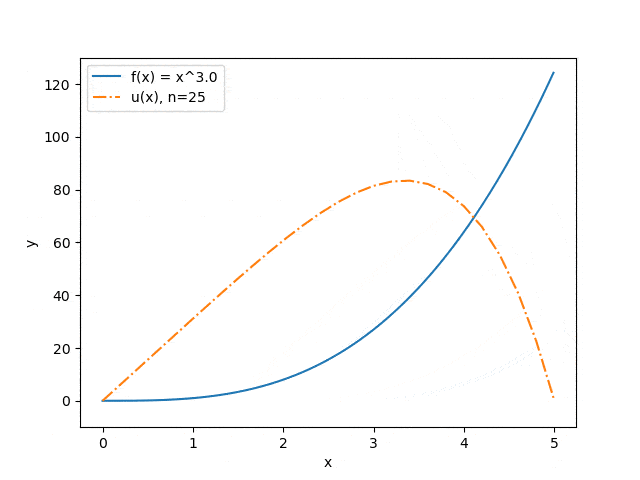
Малюнок 4 — Залежність прогнозу прогину струни від величини прикладеної сили
(анимація: 31.43 Кб, 640x480, 6 кадрів, тривалість кадру 400 мс, 10 циклів повторення)
Встановлено, що в процесі обробки кожного скінченного елемента виконується одна й та ж послідовність операцій. Така ситуація, коли потрібно виконувати однакові інструкції знов і знов для великої кількості вхідних даних, інакше кажучи SIMD (single instruction, multiple data), є сприятливою для підвищення продуктивності за рахунок графічних процесорів. Сучасні моделі домашніх центральних процесорів мають на своєму борту десятки обчислювальних ядер, в той час як відеокарти — тысячі.
Навіть у розглянутому найпростішому випадку задачі МСЕ виявлено кілька потенційних ділянок для оптимізації. По-перше, враховуючи, що рішення задачі має на увазі рішення СЛАР (системи лінійних алгебраїчних рівнянь), а кількість рівнянь може бути величезним, в контексті GPGPU (general-purpose computing on graphics processing units) очевидно напрошується розпаралелювання процесу формування матриці коефіцієнтів. По-друге, з огляду на специфіку МСЕ, можна бути впевненим в тому, що матриця коефіцієнтів буде розрідженою, а саме — трьохдіагональною. Тому пропонується відмовитися від звичного уявлення матриць у вигляді двовимірних масивів, тим самим заощадивши не тільки час виконання, а й обсяг споживаної пам'яті. По-третє, є можливість виграти на самому рішенні СЛАР, поклавши цю підзадачу на бібліотеку cuSPARSE, яка містить для цієї мети готові оптимізовані алгоритми [25].
Список джерел
- Секулович М. Метод конечных элементов / Пер. с серб. Ю. Н. Зуева; под ред. В. Ш. Барбакадзе. — М.: Стройиздат, 1993 — 664 с.: ил. — Перевод изд. Metid konacnih elemenata / Miodrag Sekulovic, 1988. — ISBN 5-274-01755-X.
- Шимановский А. Применение метода конечных элементов в решении задач прикладной механики : учеб.-метод. по собие для студентов технических специальностей / А. О. Шимановский, А. В. Путято ; М-во образования Респ. Беларусь, Белорус. гос. ун-т трансп. — Гомель : БелГУТ, 2008. — 61 с. ISBN 978-985-468-474-1.
- Finite element method [Електронний ресурс] // Google Books Ngram Viewer. URL: https://books.google.com/ngrams/graph?content=f... (дата звернення: 18.11.2020 г.).
- Метод конечных элементов [Електронний ресурс] // Google Books Ngram Viewer. URL: https://books.google.com/ngrams/graph?content=м... (дата звернення: 18.11.2020 г.).
- Courant R. Variational methods for the solution of problems of equilibrium and vibrations / R. Courant // Bull. Amer. Math. Soc, 1943. vol 49(1). — pp. 1-23.
- Hrennikoff A. Solution of Problems of Elasticity by the Framework Method / A. Hrennikoff // Journal of Applied Mechanics, 1941. — vol 7(4). — pp. 0-0.
- Argyris J. Energy Theorems and Structural Analysis: A Generalized Discourse with Applications on Energy Principles of Structural Analysis Including the Effects of Temperature and Non‐Linear Stress‐Strain Relations Part I. General Theory / J. H. Argyris // Aircraft Engineering and Aerospace Technology, 1955. — vol 27(3). — pp. 80-94.
- Clough R. The Finite Element Method in Plane Stress Analysis / R. W. Clough. — American Society of Civil Engineers, 1960. — 35 pp.
- Knepley M. Finite Element Integration with Quadrature on the GPU / M. G. Knepley, K. Rupp, A. R. Terrel // CoRR, 2016. — vol. abs/1607.04245. — 14 pp.
- Monteiro A. A computational framework for G/XFEM material nonlinear analysis / A. B. Monteiro, A. R. V. Wolenski, F. B. Barros, R. L. S. Pitangueira, S. S.Penna // Advances in Engineering Software, 2017. — vol. 114. — pp. 380-393.
- Malekan M. Two-dimensional fracture modeling with the generalized/extended finite element method: An object-oriented programming approach / M. Malekan, L. L. Silva, F. B. Barros, R. L. S. Pitangueira, S. S. Penna // Advances in Engineering Software, 2018. — vol. 115. — pp. 168-193.
- Kiran U. GPU-warp based finite element matrices generation and assembly using coloring method / U. Kiran, D. Sharma. S. S. Gautam // Journal of Computational Design and Engineering, 2019. — vol. 6(4). — pp. 705-718.
- Морозов Е. Метод конечных элементов в механике разрушения / Морозов Е. М., Никишков Г. П. — М.: Наука, 1980. — 256 с.
- Корягин Н. Пластическая деформация легких и специальных сплавов / Н. И. Корягин, А. Ф. Белов, А. С. Кузнецов и др. Пластическая деформация легких и специальных сплавов. Часть 2. — Сборник статей. — М.: Металлургия, 1982. — 201 с.
- Р. Даутов. Введение в теорию метода конечных элементов / Р. З. Даутов, М. М. Карчевский. — Учебное пособие. — Казань: КГУ, 2004. — 239 с.
- Р. Даутов. Программная реализация метода конечных элементов в МATLAB / Даутов Р. З. — Казань: КФУ, 2014. — 106 с.
- Трушин С. Метод конечных элементов. Теория и задачи / С. И. Трушин. — М.: АСВ, 2008. — 256 с.
- Алямовский А. COSMOSWorks. Основы расчета конструкций на прочность в среде SolidWorks / А. А. Алямовский. — ДМК Пресс, 2010. — ISBN 5-94074-582-2.
- Лесик Л. Демонстрационная модель деформации металла (прокатка) / Л. Н. Лесик, Н. Н. Дацун, О. А. Симоненко // Комп’ютерні програми учбового призначення: Тез. доп. II Міжнар. конф. (3-7 верес. 1994 р.). - Донецьк: ДонДУ, 1994. — с.115.
- Овсянниов В. Алгоритм построения расчетной модели участка трубопровода при прочностных расчетах в среде ANSYS / В. П. Овсянников, В. М. Оверко, П. Ф. Зима // Наукові праці Донецького національного технічного університету. Серія: гірничо-електромеханічна. Випуск 51. - Донецьк: ДонНТУ, 2002.
- Негрей С. Математическое моделирование деформационных процессов в разрушенных горных породах с помощью метода конечных элементов / С. Г. Негрей, И. Г. Сахно, А. А. Лызенко // Новые технологии подземного строительства и добычи полезных ископаемых: Материалы между-народной научно-технической конференции. - Алчевск: ДонГТУ, 2008.
- Хорошилов А. Решение двумерных краевых задач параллельным методом конечных элементов [Электронный ресурс] // Портал магистров ДонНТУ. URL: http://masters.donntu.ru/2006/fvti/horoshilov/... (дата обращения: 11.11.2020 г.).
- Климов А. Расчет барьерных целиков возле затопленных выработок [Электронный ресурс] // Портал магистров ДонНТУ. URL: http://masters.donntu.ru/2008/ggeo/klimov/diss... (дата обращения: 11.11.2020 г.).
- Скороходов Д. Исследование процесса упруго-пластической деформации непрерывнолитой слябовой заготовки методом конечных элементов [Электронный ресурс] // Портал магистров ДонНТУ. URL: http://masters.donntu.ru/2013/fmf/scorohodov/d... (дата обращения: 11.11.2020 г.).
- cuSPARSE [Электронный ресурс] // CUDA Toolkit Documentation. URL: https://docs.nvidia.com/cuda/cusparse/index.html (дата обращения: 06.10.2020 г.).
