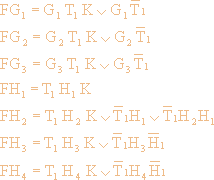Моделирование процессов в сетевых структурах
Моделирование дискретных МОП-схем
На этом уровне для описания сигнала
используются два его компонента: состояние
и силу сигнала. Наиболее естественную
интерпретацию эти аппроксимации имеют в
области моделирования дискретных схем,
изготовленных по современным МОП- и КМОП-технологиям
[2]. Считаем, что сигналы в псевдобулевой
схеме S = (H, G) имеют значения в алфавите Ln,
если логическая сила сигнала HÎ
{Ho, Ho, Hn}. Рассмотрим
ситуацию представленную на рис.2. Пусть R
сигналов напряжения - ток I1 = (n1,
i1), I2 = (n2, i2),
IR = (nR, iR)
приложены в узле P и значение выходного
сигнала в P будет I = (n, i).
Закон Кирхгофа для токов требует
суммирования токов приложенных сигналов
для получения тока выходного сигнала (n,
i). Это следует из равенства нулю
алгебраической суммы значений тока в
разветвлениях узла, т.е. учитываются их
направления и следовательно имеем:
Заменяем (1) аппроксимацией i=max{ij},
согласно которой имеем, что i есть
наиболее сильный входной сигнал и iÎI.
Эта аппроксимация может рассматриваться
как дискретный аналог закона Кирхгофа для
токов в узле для псевдобулевых схем.
Компонент напряжения n для
узла P определяется следующим образом.
Пусть V=(ni ,1, ni,2,
ni,m) есть набор
напряжений пар сигналов с наибольшим током,
т.е. (ni,1, ik), для
которыхik=max{ij}. Определим n
по следующим правилам:
1) n = U, если UÎV
или 0,1ÎV;
2) n = 0, если 0ÎV
и 1, UÏV;
3) n = 1, если0,UÏ
4) n=Z, если 0,1,UÏV.
Рассмотренные правила вычисления (n,
i) выражаются одной операцией #,
рассматривая Ln как решетку.
Оператор соединения # является
оператором наименьшей верхней границы lub
и мы можем записать (n, i) = #((n1,
i1), (nR, iR)).
Тогда Ln есть (3n+1)-значная
псевдобулева алгебра с нулем {Z, rn}
и единицей {U, r0}. Операция решетки U
эквивалентна оператору соединителя #, т. е. в
рассматриваемом случае M совпадает с #.
Графическое представление для оценки
значений сигналов в псевдобулевой алгебре
обычно отображается рисунками, которые
подобны рис.3 и используют понятие решетки
или, точнее, верхней полурешетки.
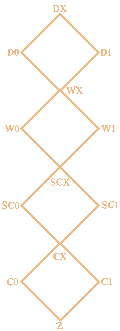Здесь используется наиболее известный алфавит
многозначных сигналов, для которых
состояния сигналов обозначаются через 0,1,X,Z
а четыре возможных силы обозначены как D
(управляемые), W (слабые), SCX (сверхзарядные)
и C (зарядные). Линии на рис.3.
соответствуют операции суммирования, т.е.
для двух сигналов на рис.3. их сумма является
сигналом, который является наименьшей
верхней гранью множества из этих элементов.
К примеру, W0ÚW1=WX, C1ÚW0=W0. Примем следующую кодировку сигналов Z=(Zh,
Zg), где Zh=(0,0,0,0) и Zg=(0,0,0),
D=(1,0,0,0), W=(0,1,0,0), SC=(0,0,1,0), C=(0,0,0,1), X=(1,0,0), 1=(0,1,0) и
0=(0,0,1). Для кодирования типов элементов
схемы (транзисторы, резисторы) используем
булев вектор T=(T1, T2).
Собственно n-МОП (p-МОП) транзистор будет
кодировать T1=1,T2=1 (T2=0), а
тип нагрузочного транзистора (заменяет
резистор в схемах МОП-технологии) через T1=0.
Тогда f0=T1T2, f1=T1T2,
f1=T1. Учитывая кодировку, E(R)=R2
и ~E(R)=R3, имеем: Ar,1=DH1ÚWH2, Ac,1=SCH3ÚCH4.
Используя R3 = ~R2 получим следующую систему уравнений.
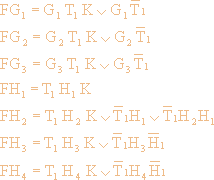
где Å - операция "исключающее
ИЛИ" и ~K = (R 2ÅT2).