Элементарная компонента нервной системы - нейрон - является сложным устройством для обработки воспринимаемой им информации и функции его полностью адекватно не определены [3,4]. Даже представление функционирования нейрона в виде оператора свертки, который дает большие возможности, является упрощающим, не говоря об обычном его представлении в виде линейного порогового сумматора по аналогии с элементами цифровой схемотехники. В [4] указано, что оператор свертки позволяет реализовать функционал Винера
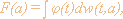
где w(t, a) - винеровская
функция броуновского движения, a
- параметр броуновской траектории. Его
использование позволяет выполнять
операции анализа спектров, прогнозирования
рядов, кодирования и декодирования. В
сущности, возможен натурный физический
эксперимент, который позволяет определить
понятие смысла для компоненты нейросети,
как интерпретации ею состояния других
компонент согласно своей модели внешнего
мира.
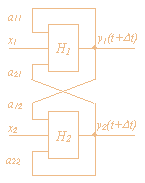
Моделирование нейронных сетей должно учитывать частотную составляющую сигналов в них, т.к., рассматривая простую схему соединения двух нейронов на рис.4 и следуя простейшей модели Hi как сумматора взвешенных сигналов в виде уравнений:
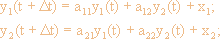
где Dt - характерное время срабатывания нейрона и aij - веса сигналов, имеем при x1 = x 2 = const:
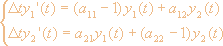(2)
Эта система эквивалентна уравнению 2-го порядка, которое имеет общее решение вида C1exp(l1t) + C2exp(l2t) + y(t), где l1, l2 - характеристические числа матрицы коэффициентов системы (2), y(t) - частное решение. Можно определить aij таким образом, чтобы решением являлись периодические движения с частотой, зависящей от Im(l) по замкнутой траектории вокруг стационарного состояния. Если рассмотреть более сложную систему взаимосвязи трех нейронов по аналогичной схеме, т.е. с обратными связями между ними, будем иметь Dtyi' = fi(y1,yn,xi); i=1,N и N=3. Известно, что, начиная c N=3 картина поведения решений системы резко усложняется [5]. В частности, возможно появление аттракторов, которые характеризуют динамику трехмерного пространства состояний и не имеют аналогов в двумерном случае.
Важным примером является моделирование
функционирования головного мозга, который
рассматривается как совокупность
взаимносвязаных нелинейных осцилляторов. У
связаных нелинейных осцилляторов возможна
внутренняя взаимосвязь между амплитудой и
фазой (или частотой) [6]. Возникает проблема
определения функции M, дискретно
суммирующей сигналы Aisinwit. Она задается пользователем,
исходя из эмпирических и физических
соображений. В случае равенства частот и
фаз всех или конечного числа групп
осцилляторов легко получить выражения для F.
Наиболее интересны для исследований
варианты самосинхронизации групп нейронов,
которые можно интерпретировать как "озарение"
и т.п.