Процесс распознавания состоит в том, что "исходный стимул" - вектор, выбранный в качестве начального условия, релаксирует в соответствии с (2) к одному из устойчивых состояний системы (2). В частности, такими векторами могут быть "образы" js.
Эволюция системы (2), (3) может быть исследована методом дискретного стохастического моделирования: либо с помощью процедуры Метрополиса и др. [17-19] (модель системы в термостате), либо с помощью алгоритма, предложенного Дж. Хопфилдом [9]. При этом вместо непрерывных переменных si вводятся дискретные, принимающие значения si0=±1, а динамика системы задается с помощью вероятности изменения состояния нейрона на каждом шаге по времени: либо в соответствии со знаком молекулярного поля Vs [9], либо в соответствии с изменением энергии системы (1), вызванным этим "переворотом", при заданной температуре термостата Т.
Возможность замены непрерывных уравнений (2), (3) дискретными связана с тем, что особая точка si=0 уравнения (2) в случае, когда V имеет вид (4), является отталкивающей. Покажем это, считая для простоты, что все js, s=1,..., so ортогональны друг другу. Линеаризуя (2) при |si|<<s0 и полагая si>eГt, из (2) получим уравнение на собственные значения ((js,s) ºåjsisi):
![]()
Этому уравнению удовлетворяют, в частности, векторы ss=js ((js,js')=dss') и собственные значения (инкременты) ГS=g1lmsN>0. Поэтому изображающая точка системы (2), (3) будет удаляться от начала координат в конфигурационном пространстве (si=0, i=1,..., N) и перейдет в область, где существенно нелинейное слагаемое в (2), т.е. |si|>s0. Конечное состояние эволюции переменной определяется, по существу, видом силы взаимодействия, испытываемой i-м нейроном со стороны остальных, - молекулярным полем (Vs)i, где si=±s0 (далее положим s0=1).
Дж. Хопфилд [9] предложил, следующий
рекуррентный алгоритм анализа динамики
ансамбля нейронов. Вводя дискретное время и
заменяя производную (2) конечной разностью,
вместо (2) полагаем
 |
(5) |
где ik£N - номер нейрона,
выбираемый случайным образом на каждом
шаге по времени, si(k)
- состояние i-го нейрона в момент
времени tk. В (5) введен также "порог
возбуждения" i-го нейрона qi,
учитывающий различия в условиях
возбуждения различных нейронов. Вместо
переменных si=±1
можно ввести также другие переменные ~si=(1+si)/2,
принимающие значения 0 или 1. Из (5) получаем
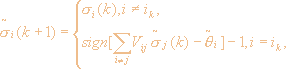 |
(5*) |
где ~qi = qi - åjVij - некоторые новые пороги возбуждения.
Уравнение (5) и (5*) были предложены в [9] для описания динамики изменения состояния ансамбля нейронов во времени. Можно, однако, представить (неупорядоченную) нейронную сеть, для которой эти уравнения описывают распространение волн возбуждения нейронов во времени и в пространстве. Действительно, рассмотрим прямоугольную решетку, в узлах которой расположены нейроны; столбцы решетки занумерованы индексом k=1, ..., К, а строки - индексом i=1, ..., N. В каждом столбце имеется "активный" нейрон, который суммирует с весами Vij сигналы, поступающие от предыдущего столбца, и может изменять свое состояние в соответствии со знаком молекулярного поля. Состояния же остальных нейронов данного столбца совпадают с состояниями на предыдущем шаге по времени нейронов предыдущего столбца, находящихся в тех же строках. Возбуждение волн в такой сети происходит путем предъявления стимула на "входе", например в первых столбцах, а устойчивые состояния уравнений Хопфилда представляют собой уединенные волны, распространяющиеся в сторону увеличения индекса k - к "выходу" из сети.
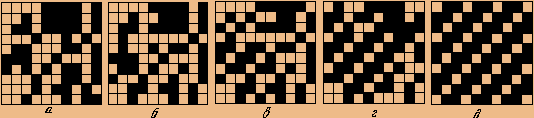
Рис. 2 - Последовательность состояний системы нейронов, возникающая в процессе релаксации исходного стимула (картинка а) в образ (картинка д), полученная при моделировании на ЭВМ уравнения (5)
Пример последовательности состояний, которые проходит система нейронов при распознавании образов в модели Хопфилда, приведен на рис. 2 (показаны некоторые промежуточные состояния), на котором левая картинка представляет собой "исходный стимул", а крайняя правая - "образ", записанный в памяти системы. При такой релаксации энергия системы (1) уменьшается, достигая с течением времени одного из локальных минимумов. Покажем, что в дискретной модели, считая, что матрица связей нейронов дается выражением (4), состояние с s=js реализует локальный минимум энергии и устойчиво, если число образов s0 невелико. Положим ss=js+ds и рассмотрим вариацию энергии (1) (mr=1, qi=0):
| (6) |
В случае, когда различные js приближенно ортогональны друг другу, второе слагаемое в (6) мало по сравнению с первым, и для вариации ds, соответствующей изменению одного из символов ±1 в образе на противоположный, первое слагаемое равно 2N, а третье 2s0. Таким образом, dE>0 - образ устойчив - при s0<N. Эта оценка качественно согласуется с результатами анализа ошибок распознавания с помощью матрицы (4), проведенного в [9, 20].
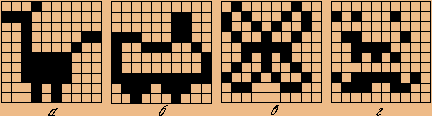
Рис. 3 - Устойчивый ложный образ (г), возникающий при распознавании стимулов ансамблем нейронов, в матрице связей которого записаны образы а-в
В процессе релаксации каждому начальному состоянию системы ("стимулу") сопоставляется один из векторов, являющийся устойчивым состоянием динамической системы (2), (3), т.е. осуществляется операция категоризации. Аналогичный процесс является важным элементом деятельности нервной системы, например зрительного тракта млекопитающих [I].
Устойчивыми состояниями уравнений
Хопфилда могут являться также векторы, не
совпадающие с js -
"ложные образы" [20, 21]. Определенный
класс таких векторов указан в [21] и может
быть построен следующим образом. Пусть s0=3,
положим
![]()
Тогда, как легко убедиться, знак i-й компоненты молекулярного поля (Vs)i совпадает со знаком jsi, если ps>0 и выполнены неравенства треугольника (достаточное условие): p1£ p2+p3, p2£ p3+p1, p3£ p2+p1.
Следовательно, j*
является устойчивой точкой алгоритма (5), не
совпадающей с js. В
случае s0=3, как можно показать,
рассмотренный класс векторов, в построении
которых наряду с образами используются
также и "негативы", исчерпывает все
ложные образы. При большем числе образов в
памяти системы число ложных образов, вообще
говоря, увеличивается. Например, для любого
нечетного s0 вектор j*,
определенный выше, является устойчивым
ложным образом (5), если сумма величин любых
рs, содержащая k=1+[s0/2]
слагаемое, не меньше суммы остальных
значений ps:
ps1+ ps2+...+ psk³ psk+1+ ps2+...+ pss0, |
(7) |
где s1,..., sk. - различные, произвольно выбранные числа (£s0). Отметим, что при s0£N появление ложных образов рассматриваемого вида может быть не связано с потерей устойчивости js.
На рис. 3 приведен пример, показывающий возникновение ложного образа в системе из N=100 нейронов, s0=3. Изображенный на рис. 3, г вектор удовлетворяет условию (7).