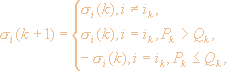
Процесс синаптической передачи нервного возбуждения между двумя нейронами является стохастическим процессом пуассоновского типа [1, 15], поскольку в силу дискретного характера выделения медиатора из синаптических пузырьков ионные токи в постсинаптической мембране и падение напряжения на ней испытывают флюктуации типа дробового шума. Поэтому можно предположить, что нейроны с некоторой вероятностью могут изменять свое состояние против направления молекулярного поля - усредненной характеристики взаимодействия нейронов в сети. В динамических уравнениях (2), (3) флюктуации потенциала учитываются ланжевеновскими случайными силами zi(t), xij(t). При моделировании процесса распознавания на ЭВМ конечную температуру термостата можно учесть методом, аналогичным [17]. В последнее время этот метод был применен для оптимизации функционалов типа энергии (1), возникающих в задаче конструирования электронных схем [18, 19].
Флюктуационная динамика системы
нейронов в методе Метрополиса и др. [17]
описывается следующим алгоритмом:
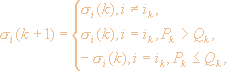 |
(8) |
где Qk=e-DEk/T, DEk=E[...,-sik, ...] - E[..., sik, ...] - изменение энергии при "перевороте спина" с номером ik; ik и Pk - случайные числа: 1£ ik£ N, 0£ Pk£ 1. При эволюции системы от выбранного начального состояния согласно (8) энергия системы (1) в среднем за большое число шагов по времени уменьшается до тех пор, пока не будет достигнуто равновесное состояние, аналогичное термодинамическому (так с большей вероятностью происходят изменения состояния нейронов, при которых DE<0). Однако на каждом отдельном шаге в отличие от алгоритма Хопфилда энергия системы может и возрастать. Моделирование эволюционного процесса (8), проведенное на персональной ЭВМ типа "Apple-11", показало, что при T=0 результаты распознавания образов согласно (8) и (5) совпадают. В частности, в случае трех образов, изображенных на рис. 3, а-в, записанных в памяти системы, устойчивым является ложный образ, изображенный на рис. 3, г. При конечной температуре термостата процесс распознавания образов по алгоритму (8) имеет две стадии. На первой из них происходит сравнительно быстрая релаксация стимула к состоянию, близкому к одному из образов. При больших температурах скорость этой стадии близка к скорости алгоритма Хопфилда (фактическое время расчетов на ЭВМ может быть в несколько раз меньше, чем по алгоритму (5)). Вторая стадия состоит в относительно медленном процессе "диффузии" системы от одного образа к другому. Скорость этого процесса определяется температурой термостата, а также существенно зависит от конкретной структуры памяти. В качестве примера на рис. 4 приведена последовательность состояний, которые проходит ансамбль нейронов в процессе диффузии по образам. В качестве образов в этом примере взяты те же векторы, что и на рис. 3. При T=0 "стимул" (рис. 4, д) релаксирует к ложному образу (рис. 4, б). При нагреве до различных температур это устойчивое состояние может переходить в разные образы (рис. 4, в-з). Таким образом, конечное состояние, в которое релаксирует стимул, зависит от "тепловой истории" системы. Эта ситуация аналогична явлению "закалки" сплавов (когда вследствие быстрого охлаждения сплавы сохраняют термодинамически невыгодную, однако устойчивую структуру) и в определенном смысле противоположна случаю "отжига" (процесса достижения полного термодинамического равновесия), рассмотренного применительно к задаче минимизации функционала типа энергии в [18, 19].
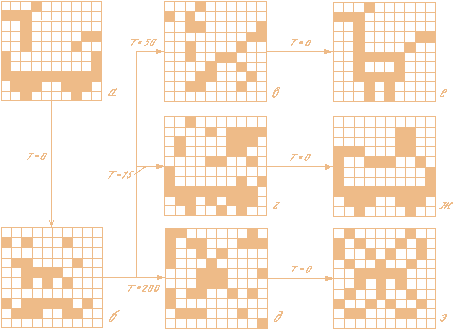
Рис. 4 - Пример последовательности изменения состояния нейронной сети при изменении температуры термостата а-исходный стимул, б -ложный образ, с, ж. з - образы, записанные в памяти
Как видно из рис. 4, в-д, повышение
температуры проходит к размытию устойчивых
образов системы. При нагреве до температуры
Т система (в том числе и механическая)
может с вероятностью w=Гe-E/T находиться
в состоянии с энергией Е (для
материальной точки в поле тяжести
приведенная формула совпадает с
барометрической формулой Больцмана для
газов). Величина Г=N!(m!(N-m)!) - число
способов, которыми в ансамбле из N
нейронов могут осуществляться состояния с
отличием от j1 в m
позициях. Наибольшая вероятность
реализуется для состояний, в которых
величина F=E-TlnГ Г, называемая свободной
энергией, достигает минимума. Чтобы оценить
степень размытия при заданной температуре,
рассмотрим случай s0=1. Свободная
энергия системы для заданного вектора s
определяется выражением (l=1)
F=-0.5*(N-2m)2-TS(m) |
(9) |
где m - хеммингово расстояние между s
и j1 (число символов
+1 или -1, отличающих эти векторы), S(m) -
энтропия состояния:
| (10) |
Минимизируя (9) с учетом (10) по m, при m<<N получим оценку:
m=N*e-2N/T,
справедливую при T<<N.
При s0=1 энергия системы (1)
достигает минимума при совпадении s
с образом, т.е. при s=j1,
либо с его негативом при s=-j1. При конечных температурах возможен
флюктуационный переход между состояниями,
близкими к образу и его негативу. Если T<<N,
то такой переход требует преодоления
энергетического барьера
DF» F(m=N/2) - F(m=0) = - NTln2 + 0.5N2 |
(11) |
Вероятность такого перехода можно
оценить из выражения, аналогичного
выражению для вероятности образования
зародыша при фазовом переходе:
w» N*e-DF/T = N2N*e(-0.5N2/T) |
(12) |
Из (12) видно, что при низких температурах вероятность перехода оказывается малой, однако с повышением Т величина барьера уменьшается и при Т³Tk»N обращается в нуль. При Т³Tk происходит свободная "диффузия" ансамбля нейронов между различными состояниями.
С увеличением числа образов s0
ситуация существенно усложняется.
Рассмотрим случай s0=2. Пусть
векторы образов (j1 и
j2 имеют N1
совпадающих компонент, N2
несовпадающих, N1 + N2 = N.
Энергия произвольного состояния системы
нейронов s дается
выражением
| E=-0.5*[(N1-2m1+N2-2m2)2+(N1-2m1-N2+2m2)2]=-[(N1-2m1)2 + (N2-2m2)2], | (13) |
где m1 - число отличий s
и j1 в первой
группе компонент, a m2 - во
второй. Энтропия такого состояния равна
| (14) |
Из (13), (14) получаем выражение для
свободной энергии системы в виде суммы двух
независимых слагаемых:
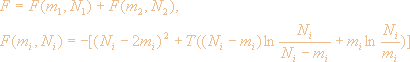 |
(15) |
Эти выражения определяют две характерные температуры:
Tk1=N1/ln2º Tk(1+p), Tk2=N2/ln2º Tk(1-p),
где p=(N1-N2)/N. Если N1
и N2 не близки друг к другу (например,
N2>N1), то при повышении
температуры характер динамики системы
может испытывать два резких превращения.
При T<Tk1<Тk2 ансамбль
нейронов находится в состоянии, близком к
одному из векторов j1, j2
или их негативам (и релаксирует к одному из
этих состояний в процессе распознавания
образов). При N³Tk1
возникают случайные блуждания между j1
и j2, при этом группа
из N2 компонент s
близка к совпадающим компонентам векторов j1
и j2. Наконец, при T>Tk2
начинаются блуждания между образами и их
негативами. Фазовая диаграмма системы в
переменных T, р приведена на рис. 5.
Низкотемпературная область отвечает
упорядоченному, "кристаллическому"
состоянию, высокотемпературная - "жидкому",
а промежуточные области можно назвать "жидкокристаллическими",
поскольку для промежуточных областей имеет
место ситуация, характерная для
жидкокристаллического состояния, когда
одна часть степеней свободы системы
является заторможенной, а другая часть
находится в "расплавленном" состоянии.
На рис. 6 приведен пример пары образов, для
которых при моделировании на ЭВМ в
определенном интервале температур
наблюдалось "промежуточное" состояние
- случайные перескоки элемента М в N
и обратно. При низких температурах
перескоки заторможены, а при повышении
температуры диффузия по различным
состояниям системы происходит свободно.
|
|
|
|
Рис.5. Фазовая диаграмма системы нейронов, в памяти которой записаны два образа, p=(j1, j2)/N |
Рис. 6. Пример пары образов, между которыми при моделировании на ЭВМ в определенном интервале температур наблюдалось "блуждание" |