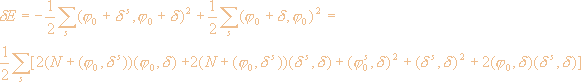
При увеличении числа образов,
записываемых в память системы, минимумы
энергии (1), отвечающие различным js,
могут сливаться. Рассмотрим группу образов js(s=1, ..., s0),
получающихся при небольших случайных
искажениях ds
некоторого вектора j0
(при этом группа не содержит самого
исходного вектора): js=j0+ds.
Покажем, что вариация на величину d
вектора j0 приводит
к изменению энергии, соответствующей этому
вектору, на величину
 |
(16) |
При 2m=-(j0, ds)<<N, s0>>1 и случайном искажении исходного вектора j0 при построении группы образов может выполняться неравенство dE³0, и, следовательно, исходный вектор отвечает минимуму энергии системы. В психологии образ, аналогичный j0 (т.е. являющийся в определенном смысле усреднением некоторого числа образов и остающийся в памяти человека наряду с действительно предъявляемыми образами), получил название "прототипа" [З]. Пример образования прототипа при предъявлении группы образов приведен на рис. 7.

Рис. 7. Примеры возникновения
прототипа в системе нейронов
а - исходные
девять образов, б - прототип при
расположении нейронов в решетки, причем
взаимодействуют лишь нейроны, находящиеся
в соседних узлах ансамбля взаимодействуют
между собой
Вероятность появления прототипа при записи данной группы образов в матрицу V можно охарактеризовать относительной частотой появления вектора, отвечающего прототипу, в качестве устойчивой точки алгоритма (5) или (5*). На рис. 8 приведены гистограммы, показывающие относительную частоту появления в качестве устойчивых образов векторов, отличающихся от j0 в m0 компонентах, в зависимости от числа записываемых образов s0. Из этого рисунка видно, что относительная частота появления прототипа мала при небольшом числе образов s0 и достигает примерно 75% при s0 >0.2N.
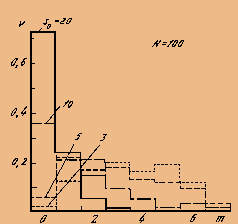
Рис. 8. Гистограммы, показывающие относительную частоту v появления устойчивых векторов алгоритма (5*), отличающихся от прототипа в m компонентах, в зависимости от числа записанных образов S0
Вычислим вероятность того, что при записи
s0 случайных векторов в матрицу V,
отличающихся от j0 в m0
позициях, j0 будет
реализовывать минимум энергии системы, т.е.
будет выполнено условие dE³0.
Из (16) получаем, что dE³0
при
| (17) |
(предполагается, что N, m0 >>1).
Распределение вероятности величины х
дается функцией распределения
| (18) |
где xs= s0-1(d,ds), а угловые скобки означают усреднение по векторам ds, имеющим в m0 позициях ±2, а в остальных позициях - нули. Вычисляя среднее в предположении, что +2 и -2 встречаются в ds равновероятно:
![]()
и подставляя его в (18), получим
| (19) |
При s0>>1 можно разложить
косинус в ряд Тейлора и, ограничиваясь
первыми двумя членами, получить
приближенное выражение
| (20) |
Вероятность того, что x£2,
дается интегралом вероятности
| (21) |
Из выражения (21) видно, что вероятность возникновения прототипа тем больше, чем меньше m0 (при заданном отношении s0/ N) или чем больше образов s0 (при заданном m0/ N) использовалось для его формирования.
Возможность рассмотрения явления выработки прототипа как процесса статистического усреднения по ансамблю образов, связана с видом матрицы связей между нейронами V (4), которая линейна по числу образов в памяти s0. Отметим в этой связи, что матричным элементам Vij (4) и энергии Е (1) может быть придан непосредственный вероятностный смысл, если воспользоваться понятием фрустрации ("разочарования") связей, впервые введенным для описания взаимодействующих спинов в неупорядоченных магнитных сплавах - спиновых стеклах [22]. Действительно, согласно (4) матричный элемент Vij может быть записан в виде разности двух неотрицательных чисел:
![]()
Здесь V+ij - число образов js, для которых jsi=jsj, a V-ij - число образов с jsi=-jsj. Поскольку V+ij+V-ijєs0, то v+ij и v-ij имеют смысл вероятности соответственно корреляции и антикорреляции i-го и j-го нейронов в рассматриваемом ансамбле образов памяти. По аналогии с [22] связь (ij) между i-м и j-м нейронами в произвольном состоянии нейронной сети естественно назвать фрустрированной ("разочарованной"), если (v+ij - v-ij)sisj <0, и нефрустрированной при противоположном знаке неравенства. Тогда энергия системы (1) запишется в виде: E=0.5s0QF(s), где QF(s) - разность между числами фрустрированных и нефрустрированных связей. Векторы, отвечающие минимуму энергии системы, соответствуют, таким образом, наибольшему числу нефрустрированных связей, т.е. наименьшей вероятности фрустрации нейронной сети.