
Рассмотрим вначале ОНС, состоящие из
осцилляторов Ван-дер-Поля [88, 89, 123].
Предполагается, что эти осцилляторы слабо
нелинейные (почти гармонические), их
динамика описывается уравнениями
 |
(2.5) |
гдеht - белый шум.
Система двух таких осцилляторов с разностью собственных частот Dw и величиной связи G изучалась в работе М. Охсуги и др. [88]. Аналитическими методами были получены границы трех областей на плоскости (Dw, G): область 1 - квазипериодические двухчастотные колебания (биения); область 2 - затухающие колебания (стационарное состояние); область 3 - взаимная синхронизация. Рассматривался также случай синусоидального внешнего воздействия на каждый из осцилляторов. Численные эксперименты с этой системой показывают, что в ней существуют два режима: сильная синхронизация и неточная синхронизация, когда амплитуды осцилляторов демонстрируют модулированные колебания.
Сеть из трех осцилляторов Ван-дер-Поля рассматривалась в работе С. Оматы и др. [89]. Осцилляторы были соединены по типу "общего источника", когда каждый из двух одинаковых взаимодействующих осцилляторов получает сигнал от третьего, отличного от них, осциллятора. Компьютерные эксперименты и математическое исследование показали, что при увеличении разности в величинах воздействия (величины расстройки) происходит переход от режима с одним устойчивым состоянием к режиму с двумя устойчивыми состояниями. В последнем случае удается провести исследование гистерезисных кривых.
В работе Е. Ямагучи и X. Шимизу [123] была разработана теория самосинхронизации для системы N осцилляторов Ван-дер-Поля (2.5) с распределенными частотами и внешними шумами. Вопрос о синхронизации рассматривался в смысле (ОС 2) в терминах макрохарактеристики системы
![]()
(параметр порядка). С ее использованием
были найдены условия, при которых в системе
происходит синхронизация колебаний с
частотой, равной усредненной. Для этого
выведено приближенное уравнение динамики
параметра порядка:
![]()
Если с1 - отрицательная величина, то устойчивым является стационарное состояние X=0 и в системе не появляется синхронного коллективного поведения. Если же с1>0, то устойчивыми стационарными состояниями будут:
![]()
Эти условия удалось подробно проанализировать в терминах параметров осцилляторов для различных распределений собственных частот. Оказалось, что в этих терминах существуют два типа бифуркаций: механическая бифуркация, зависящая от ширины распределения собственных частот осцилляторов в присутствии внешних шумов, и тепловая бифуркация, зависящая от дисперсии шума при равенстве собственных частот. Численные эксперименты показывают, что имеет место бифуркация типа Ландау, объединяющая как механическую так и тепловую бифуркации.
Рассмотрим теперь сети фазовых
осцилляторов с синусоидальным
взаимодействием. Динамика такой сети
описывается уравнениями
|
(2.6) |
где qi, - текущая фаза i-го осциллятора, (wi - его собственная частота, К - константа связи (К > 0).
Если все частоты в уравнениях (2.6) одинаковы, wi=w, то эта система известна в физике как классическая XY-спиновая модель с нулевой температурой [71,73].
Нас будет интересовать случай, когда собственные частоты wi различны. Если разброс собственных частот wx ограничен и достаточно мал, то имеет место синхронизация всех осцилляторов сети в смысле (ОС1). Удобная форма описания поведения фаз получается при расположении осцилляторов на отрезке [0,1] и переходе к пределу при N®Ґ. В этом случае (2.6) принимает вид:
![]()
Как показано в работе Г. Эрментраута [37], после установления режима синхронизации фазы принимают вид q(x,t)=wt+j(х), что соответствует синхронизации на средней частотеw. Соотношение фаз разных осцилляторов задается функцией j(х).
Исследование синхронизации в системе (2.6) в смысле ОС 2 имеет гораздо более сложный характер. Пусть g(w) - плотность распределения собственных частот осцилляторов, где g - достаточно гладкая функция, симметричная относительно w0. Поскольку все фазы могут быть сдвинуты на w0 t при сохранении вида уравнений (2.6), то без ограничения общности можно считать, что w0=0.
Чтобы исследовать синхронизованность
осцилляторов (2.6), в книге Е. Курамото [74]
предлагается рассматривать комплексную
величину Z(t), называемую фазовым
параметром порядка:
| (2.7) |
Эта величина вводится по аналогии с термодинамическими фазовыми переходами для описания макроскопического состояния системы.
Если оказывается, что в сети с бесконечно
большим числом осцилляторов существует
предел
limt®ҐZ(t)= Z |
(2.8) |
и |Z|¹0, то можно говорить о том, что в сети возникла синхронизация.
С использованием параметра порядка Z(t)
система уравнений (2.6) приводится к виду:
| (2.9) |
В предположении существования предела (2.8)
можно формально рассматривать (2.9) как
систему независимых уравнений,
стационарные решения которых явно
находятся в зависимости от неизвестной
постоянной Z. В свою очередь,
подстановка стационарных решений q1,...qN
уравнений (2.9) в формулу (2.7) дает уравнение
для определения Z вида
Z = S(X, Z). |
(2.10) |
При малых |Z| это уравнение может быть
проанализировано на предмет наличия у него
решений в зависимости от К. Результат
этого анализа таков. Пусть g(w) выпукла
вверх в точке w=0. Существует
критическое значение К, равное КC
= 2/pg(0), такое что при К<Kc
(2.10) имеет единственное нулевое решение, а
при К³Ks от
ветви нулевого решения отделяется ветвь
нового решения, имеющего вид:
| (2.11) |
Здесь
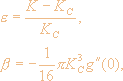
q - произвольная постоянная, e предполагается малым. Таким образом, в точке К=КC имеется фазовый переход. Этот результат был получен в работе Е. Курамото и И. Нишикавы [75]. В работе X. Сакагучи и Е. Курамото [93] имеется его обобщение на случай, когда взаимодействие осцилляторов задается функцией sin(qj-qi-a) при a¹0. Для плотности равновесного распределения частот в этом случае в [93] также выведена приближенная формула.
Вопрос об устойчивости решений уравнения (2.10) решается путем вывода динамического уравнения для Z(t), которое учитывает флуктуации макропараметра Z(t) в зависимости от микроскопических переменных q1(t),...,qN(t). Такое уравнение в приближенной форме выведено в [75]. Оно показывает, что при e<0 нулевое решение устойчиво
| Z(i)| ~ 1/(|e|t).
В области сильных связей (e>0) нулевое решение теряет устойчивость. Устойчивым становится решение (2.11), причем
![]()
где g0>0.
Следует отметить, что значение Zst получено при условии (2.8), которое при конечных значениях N выполняется лишь приближенно, поскольку на Z оказывают влияние флуктуации фаз осцилляторов. В связи с этим представляло интерес получить оценки амплитуды флуктуации Z
h= <|Z - <Z>|2>.
Эта задача была решена в работе [75] и в работах X. Даидо [31,32]. В [75] выведена формула для h, справедливая вдали от критической точки Кc,
h = Nd/N2,
где Nd - число несинхронизованных осцилляторов. Вблизи критической точки оценки имеют вид [31,32]: <|Z - <Z>|2> ~ 1/N|K - KC|-a,
где a=1/2 для подкритического случая (К<Кc) и a=1/8 для надкритического случая (К>Kc). Этот результат хорошо согласуется с численными экспериментами по определению флуктуации параметра Z в окрестности критической точки, выполненными X. Даидо [29].
Одна из модификаций системы (2.3) - сеть из осцилляторов с контролируемым напряжением (VCON - Voltage Controlled Oscillator Neuron), предложенная Ф. Хоппенштедтом [53-55] в качестве колебательной модели нейрона. 2p-периодические функции связи между нейронами Hk(q1,...,qN) выбираются так, чтобы учесть наиболее важные аспекты изучаемого процесса и упростить вычисления.
Для исследования синхронизации Ф. Хоппенштедт предложил метод вектора вращения [53,54]. Рассмотрим сеть фазовых осцилляторов типа (2.3) в более общем виде, не предполагая парности взаимодействия:
![]()
Выберем ортогональный базис в пространстве ÂN: w, S2, ..., SN и введем новые переменные v, u2, ..., uN:
v=wq, uj = Sjq, j=2,...,N,
(Sjw=0, SjSk=0 для j¹k)
Уравнения для фаз qk в новых переменных будут иметь вид:
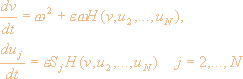
Таким образом, малый параметр e позволяет перейти к одной быстрой переменной v (v ~ w2t) и медленным переменным uj, что необходимо для применения метода усреднения и дальнейшего анализа системы. После усреднения по v
![]()
уравнения преобразуются к виду
![]()
Доказано, что если существует асимптотически устойчивое стационарное состояние усредненной системы (u®u* при t®Ґ), то исходная система будет синхронизоваться в смысле ОСЗ.