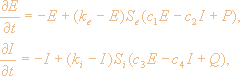
При рассмотрении ОНС с локальными связями предполагается, что осцилляторы расположены в узлах d-мерной целочисленной решетки (d = 1, 2, 3, ...), и каждый осциллятор имеет связи только с осцилляторами из своей окрестности фиксированного радиуса. Обычно это связи с 2d ближайшими соседями. При d=1 сеть называется цепочкой осцилляторов. Иногда рассматривается замыкание цепочки в кольцо.
Работы, посвященные ОНС с локальными связями, можно разделить на две группы. В первой из них изучаются сети со слабыми связями, а осцилляторы образуют цепочку или кольцо. В других работах изучаются сети с сильными связями, а размерность сети может быть произвольной. И в том, и в другом случаях исследование сводится к сетям фазовых осцилляторов. Мы последовательно опишем оба эти подхода, но прежде, чем перейти к этому, приведем три результата, относящиеся к осцилляторам общего вида.
Первый из них касается условий существования колебательных режимов в сети локально взаимодействующих осцилляторов. В работе Г. Эрментраута и Н. Копель [40] показано, что в ряде случаев в такой системе могут отсутствовать колебания, а устойчивым режимом будет положение равновесия. Подчеркивается, что для случая больших связей неправомерно рассматривать фазовые уравнения, получаемые усреднением по циклу в предположении слабых связей. Например, для двух осцилляторов Вилсона-Коуэна с возбуждающими связями (см. (2.12)) показано существование устойчивого положения равновесия. Несмотря на то, что каждый из осцилляторов сам по себе способен демонстрировать колебания, достаточно большие связи могут подавить колебания. (Этот эффект обратен известным наблюдениям Тьюринга и Смейла, которые строили колебательные системы из неколебательных элементов.) Как следует из работ Г.Н. Борисюк и др. [20] и А.И. Хибника и др. [62], в случае сильных возбуждающих связей двух осцилляторов Вилсона-Коуэна существуют устойчивые торы в четырехмерном фазовом пространстве, и система демонстрирует двухчастотные колебания.
Второй результат приведен в работе Г. Эрментраута [38] и касается идентичных осцилляторов на кольце. Связи между ближайшими соседями предполагаются линейными и слабыми, а параметры выбираются так, чтобы каждый осциллятор имел предельный цикл вблизи бифуркации Хопфа. Тогда существует семейство решений, которые в полярных координатах имеют вид:
rj = Rl, qj = Wlt
+ jjl,
где j = 1,...,N - номер осциллятора на
кольце; jl=2pl/N, l=0,1,...,
(N-1) - номер решения (волны); Rl, Wl
- постоянные, не зависящие от времени.
Приведенные в работе условия устойчивости найденных решений показывают, что при общих условиях будут устойчивыми волны с меньшими волновыми числами. В работе рассмотрено также обобщение на случай нелинейных и нелокальных связей и проведено сравнение поведения волн при различных типах связей.
Третий результат относится к численному
исследованию динамических режимов
однородной цепочки осцилляторов Вилсона-Коуэна
с локальными связями, проведенному P.M.
Борисюком и А.Б. Кирилловым [24]. Отдельный
осциллятор Вилсона-Коуэна [120] описывается
системой уравнений:
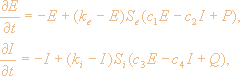 |
(2.12) |
Показано, что в системе при изменении величины внешнего входа и силы взаимодействия между осцилляторами наблюдаются следующие режимы: режим стационарной фоновой активности; режим регулярных колебаний с постоянным сдвигом фазы между соседними осцилляторами; режим двухчастотных колебаний; режим стохастических колебаний. На бифуркационной диаграмме указаны границы между режимами, что дает возможность управлять поведением системы. Обсуждаются также вопросы о взаимодействии бегущих волн и о самоорганизации долгоживущих кластеров высокой фоновой активности при условии, что входы на осцилляторы неоднородны и случайно выбраны.
В серии работ Н. Копель и Г. Эрментраута [39,67,69,70] рассматриваются цепочки фазовых осцилляторов со слабыми связями. При малых коэффициентах связи e фазовые осцилляторы получаются из осцилляторов общего вида
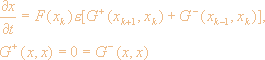
с помощью техники, описанной в начале
этого раздела. Уравнения на инвариантном
торе будут иметь вид:
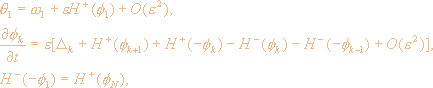 |
(2.13) |
Система (2.13) считается синхронизованной, если все осцилляторы имеют одинаковые частоты и фиксированные во времени разности фаз fk.
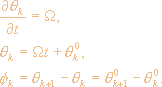
Поэтому вопрос о синхронизации сводится к
исследованию стационарных решений
уравнения (2.13):
Dk + H+(fk+1 ) + H+(-fk ) - H-(fk+1 ) - H-(-fk-1 ) = 0. |
(2.14) |
В работе [39] рассматривается случай линейного затухания собственной частоты осцилляторов вдоль цепочки. Показано, что при небольшом градиенте частоты существует решение уравнений (2.14), т.е. возможна синхронизация системы. Если же градиент становится достаточно большим, то синхронизация невозможна. При этом в системе (2.13) появляется предельный цикл большой амплитуды (порядка 1, рождается из сепаратрисного контура двух седел), который соответствует наличию в системе двух "частотных плато", другими словами, цепочка распадается на две подцепочки, такие, что осцилляторы в левой подцепочке имеют одну и ту же частоту и осцилляторы в правой подцепочке также имеют одну и ту же, но уже другую частоту.
В работе [67] рассматриваются длинные цепочки осцилляторов (N®Ґ). В этом случае исследование уравнения (2.13) осуществляется путем сведения его к краевой задаче.
Выделим нечетную и четную части функций Н±(f):
Н±(f) =
Н±0(f)
+ Н±e(f),
где
Н±0(-f)=-Н±0(f), Н±e(-f)=Н±e(f),
и определим функции f и g как
f = 0.5(Н+e + Н-e) + 0.5(Н+0 - Н-0),
g = 0.5(Н+0 + Н-0) + 0.5(Н+e - Н-e).
Кроме того, обозначим bk=NDk.
Тогда уравнение (2.14) можно записать в виде:
| (2.15) |
Предположим, что b(х), f(х) - гладкие функции х на отрезке 0£х£1 такие, что
bk=b(K/N),
fk=f (K/N).
Тогда при N®Ґ f(х)
удовлетворяет уравнению
b(x) + 2f(f)x+ g(f)xx/N= 0 |
(2.16) |
с граничными условиями
f=g при x=0 и f=-g при х=1.
Заметим, что полученная краевая задача является сингулярно возмущенной с малым параметром при старшей производной. Кроме того, уравнение (2.16) не принадлежит к классу уравнений реакция-диффузия, которые обычно возникают при переходе к непрерывным уравнениям: это уравнение является эвристической аппроксимацией для (2.15).
В [67] доказана теорема, что при выполнении определенных ограничений на функций b, H+, Н- (и, следовательно, на f и g) существует решение уравнения (2.15), которое при N®Ґ сходится к решению уравнения (2.16). Причем для уравнения (2.13) это стационарное решение является устойчивым.
Итак, для уравнения (2.13) при больших N показано существование устойчивого стационарного решения. Для построения этого решения изучается краевая задача с малым параметром при старшей производной. Как обычно, в таких задачах решение будет содержать пограничный слой. При условии однородности связей пограничный слой будет располагаться в середине отрезка, но небольшим возмущением его легко можно сместить к одному из концов. Такое свойство решений позволяет авторам построить модель центрального генератора паттернов (см. раздел 5).
В работе [69] рассматриваются длинные цепочки слабо связанных осцилляторов при более общих условиях, чем в [67]: допускаются немонотонные изменения собственных частот осцилляторов, неоднородность в связях вдоль цепочек в одном и другом направлениях и более общий вид функции взаимодействия.
Здесь также рассматривается случай N®Ґ, который приводит к сингулярной граничной задаче на отрезке [0,1]. Для укороченного уравнения существуют три типа решений:
Также рассматриваются случаи введения локальных изменений собственных частот и величин связи и их последствия. Как правило, локальные изменения имеют локальное влияние на решения и не распространяются на всю цепочку.
В работе [70] рассматривается обобщение на случай множественных связей. Здесь предполагается, что каждый осциллятор длинной цепочки (N®Ґ) связан с m осцилляторами слева и m осцилляторами справа, где m мало по сравнению с N. В этом случае также существуют решения, соответствующие фазовой синхронизации системы, которые в основном соответствуют случаю ближайших соседей.
Перейдем теперь к сетям фазовых
осцилляторов с сильными локальными связями.
В случае синусоидального взаимодействия
уравнения динамики имеют вид:
| (2.17) |
В случае нормального распределения g и связей с ближайшими соседями с помощью нестрогих рассуждений и моделирования на ЭВМ X. Сакагучи и др. [94] показали, что указанная синхронизация возникает при d>2 и не может возникнуть при d£2, поскольку в последнем случае фазы осцилляторов, расположенных далеко друг от друга, будут "разбегаться".
В общем случае, когда взаимодействие осцилляторов регулируется достаточно произвольной функцией, а распределение g не обязательно нормально, получить нижнюю оценку для критической размерности существенно труднее. Это удалось сделать X. Даидо [30], который использовал метод перенормировки (см. [78]). Гиперкуб в Âd содержащий сеть, разбивается на подкубы. Каждому подкубу ставится в соответствие новый осциллятор, фаза которого равна средней фазе осцилляторов, расположенных в этом подкубе. После некоторой перенормировки времени и фаз новых осцилляторов уравнения для этих фаз становятся почти такими же, как для исходных осцилляторов. Важное отличие состоит в том, что теперь параметр взаимодействия будет равен
![]()
где b
зависит от размерности d и параметра a,
характеризующего скорость убывания хвоста
плотности g (a=2 для
нормального распределения и 0<a<2,
если дисперсия собственных частот
осцилляторов бесконечна),
b = 1 - 1/a - 1/d.
Несложный анализ показывает, что синхронизация новых осцилляторов может иметь место лишь при b³0. Отсюда следует, что
d³a/(a-1), где 1<a£2,
а при a£1 синхронизация невозможна ни при какой размерности d. Заметим, что при a=2 оценка d³2 все же хуже, чем d>2, полученная в [94].
Информация о строении кластеров синхронизованных осцилляторов содержится в работе С. Штрогатца и Р. Миролло [115]. Оказывается, что если собственные частоты осцилляторов распределены нормально, то эти кластеры имеют очень рыхлое, губчатое строение: вероятность того, что такой кластер содержит куб размера порядка N, при N®Ґ экспоненциально убывает до 0.