Laboratory.Ru
сборник трудов по науке и
технике
|
Laboratory.Ru |
|
Л. П. Костина, канд. физ. - мат. наук.
(Санкт -
Петербургский государственный университет).
Показано, что необходимость принципиально новой трактовки проблемы распределения нескладируемых ресурсов на сетях обусловлена объективно существующей закономерностью, состоящей в том, что при переходе каждой единицы ресурса с одной работы на другую между этими работами возникают связи по использованию одного и того же ресурса. Поскольку возможны различные варианты указанных связей, то данная задача обусловлена переменной структурой графа.
Согласно теореме о критических путях сетевой модели, отображающей многопроектную разработку с учетом ресурсов следует, что в данном случае проблема состоит не в получении календарного плана работ на основании известных сетевых графиков, каждый из которых определяется технологией и принятой организации работ в проекте, а в определении сетевой модели, отображающей многопроектную разработку с учетом ресурсов (ресурсного графа) при соблюдении технологии проектирования каждого проекта в качестве ограничения.
Страница 1
Страница 2
Страница 3
1. Введение
Одним из важнейших вопросов, возникающих при создании автоматизированных систем управления сложными системами, является выбор приемлемых моделей для описания управляемых процессов. Многие исследователи пришли к выводу, что наиболее приемлемой моделью является сетевая модель комплекса работ. Такой вывод обосновывается многими соображениями, которые изложены в обширной литературе. Решение проблем совершенствования управления в самых разных сферах народного хозяйства связывали с сетевыми методами планирования и управления (СПУ), появление которых в управлении единогласно было признано шагом вперед по сравнению с ленточными графиками Ганта. Аппарат CПУ предназначен для решения двух основных проблем: формирования календарного плана реализации комплекса работ и принятия эффективных решений в процессе выполнения этого плана.
Указанное свойство сетевых методов становится особо значимым при управлении сложными системами, которые обусловлены необходимостью выполнения нескольких крупных объектов одновременно. Важнейшей задачей при этом является не только составление календарного плана с учетом рационального распределения людских ресурсов и оборудования во времени и между отдельными объектами, но и возможность его контроля и регулирования методами сетевого планирования и управления. Очень важно чтобы инструмент контроля был бы приспособлен к постоянно меняющейся обстановке, а для этого нужны действенные методы, позволяющие алгоритмизировать процессы управления.
Существующие решения задач распределения ресурсов на сетях обеспечивают исключительно функции планирования. Все известные теории абсолютно беспомощны перед стохастическими сетями, а также сетями большой размерности, так как методы их решения базируются на комбинаторике, которая приводит либо к анализу практически бесконечного числа вариантов, либо к привлечению эвристики. Поэтому основные проблемы сетевого планирования и управления с учетом ресурсов так и остались нерешенными.
В работе [1] констатируется, что в настоящее время в научной литературе внимание в основном уделяется задачам загрузки оборудования и построению расписаний [2 - 7]. В работе [8] дается обстоятельный анализ решения указанного класса задач, где список литературы содержит 122 наименований работ.
2. Обоснование необходимости нового подхода
Одной из причин угасшего интереса является неудачные попытки ввести в сетевое планирование и управление нескладируемой ресурс. Основной недостаток традиционных методов решения задач распределения ресурсов на сетях относится к постановке, которую нельзя считать удачной. Стремление к упрощению сложности задачи распределения свело на нет возможности сетевых методов планирования и управления.
Замечания по поводу общепринятой постановки проблемы распределения ресурсов на сетях в научной литературе приводились и ранее. "Несомненно, даже в тех случаях, когда ограничения, связанные с ресурсами с самого начала принимаются во внимание и находят отражение в сетевом графике, этот учет происходит далеко не наилучшим образом" [9. c 41]. И далее в этой же работе: "При разработке больших проектов и в особенности многопроектных задач (требующих распределения общих ресурсов между работами параллельно осуществляемых проектов) даже отыскание допустимого плана без специальных алгоритмов становится затруднительным.
Однако даже в тех случаях ( наиболее простых ), когда
интенсивности ![]() , (а потому и длительности
, (а потому и длительности ![]() для всех работ постоянны) рассматриваемым
задачам не удается придать удовлетворительную математическую формулировку" [9. c
75].
для всех работ постоянны) рассматриваемым
задачам не удается придать удовлетворительную математическую формулировку" [9. c
75].
Предложенные постановки оптимизационных задач можно разбить на два основных класса: при заданных ограничениях на ресурсы минимизация суммарного отклонения расчетных сроков выполнения целевых событий от директивных и оптимального в определенном смысле использования ресурсов при заданной продолжительности комплекса работ ( равномерная загрузка ресурсов).
При этом нет принципиальной разницы в подходах к решению указанных классов задач. В обоих случаях прежде чем приступить к распределению ресурсов производят расчет сетевых графиков, каждый из которых построен на основании технологии и принятой организации операций по каждому проекту. Затем полученные таким образом показатели (чаще всего полные резервы времени операций, либо их начальные сроки) используются для определения коэффициентов приоритетности с целью обеспечения операций ресурсами и получения расписания их выполнения в планируемом периоде времени [10 - 22].
Общепринятая точка зрения зафиксирована в словаре-справочнике [20]. На стр. 488 констатируется "Все операции, не принадлежащие критическому пути, можно сдвинуть во времени в пределах их резервов, не увеличивая при этом общей продолжительности комплекса. Это свойство широко используется при определении плановых сроков начала операций с учетом наличия ресурсов и соображений надежности выполнения формируемого плана".
Различие при этом состоит лишь в способе определения плановых сроков начала операций в пределах их резервов. Так, например, в работах Д. И. Голенко и его последователей для этого используется метод статистических испытаний, иначе называемый методом Монте-Карло [21]. Большинство авторов предпочтение отдают аналитическим методам. Но неизменным при этом остается предпосылка, что резервы времени операций известны, так как известна топология сетевой модели, которая определяется технологией и принятым порядком ведения операций по каждому проекту. Указанный подход к решению задач распределения ресурсов на сетях был рекомендован для разработчиков АСУ в документе [22]. Покажем необоснованность традиционных решений путем анализа примера работы [10].
При решении задачи распределения ресурсов по любому из принимаемых критериев автор работы [10] видит проблему в нахождении расписания выполнения операций при фиксированной топологии сетевого графика. По мнению автора цель любой процедуры сглаживания профиля ресурсов состоит в планировании всех некритических операций в допустимых пределах.
Все же критические операции всегда планируются в первую очередь.
В [10. c 254] по этому поводу утверждается: "Существенным моментом является то, что при разработке сглаживания расписания изменяются начальные моменты только для некритических операций. В результате длительность проекта не увеличивается". Несправедливость этих утверждений следует из опровергающего примера 1.
Пример 1. На
выполнение операций, представленных в сетевом графике на рис.1 выделено 7
человек. Все операции могут производиться с постоянной интенсивностью
потребления ресурсов. Число ресурсов для каждой операции фиксировано. В таблице
1 представлены исходные данные решения задачи, где i - номер начального события; j - номер конечного события; ![]() - продолжительность операции;
- продолжительность операции; ![]() трудоемкость операции в чел/дн.;
трудоемкость операции в чел/дн.; ![]() требуемое число людских ресурсов.
требуемое число людских ресурсов.
Таблица1. Исходные данные.
| i | j | t(i,j) | D(i,j) | n(i,j) |
| 1 | 2 | 3 | 3 | 1 |
| 1 | 3 | 9 | 27 | 3 |
| 1 | 5 | 11 | 33 | 3 |
| 2 | 4 | 2 | 2 | 1 |
| 3 | 5 | 5 | 20 | 4 |
| 4 | 5 | 6 | 18 | 3 |
В таблице 2 представлены результаты решения примера методом, предложенным Х. Ахьюджа, когда на третьем шаге распределения ресурсов предпочтение отдано операции (3,5), которая в сетевом графике рис.1 находится на критическом пути, а не операции (4,5), имеющей резерв времени.

Рис.1.
Таблица 2. Результаты решения примера для 1-го варианта распределения
| i |
j |
ДНИ | ||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | ||
| 1 | 2 | 1 | 1 | 1 | ||||||||||||||
| 1 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | ||||||||
| 1 | 5 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | ||||||
| 2 | 4 | 1 | 1 | |||||||||||||||
| 3 | 5 | 4 | 4 | 4 | 4 | 4 | ||||||||||||
| 4 | 5 | 3 | 3 | 3 | 3 | 3 | 3 | |||||||||||
Рассмотрим другой возможный вариант распределения этих же ресурсов, отдав предпочтение на третьем шаге операции (4,5), имеющей резерв времени, а не операции (3,5), лежащей на критическом пути. Результаты этого случая представлены в таблице 3.
Таблица 3. Результаты решения примера для 2-го варианта распределения.
| i |
j |
ДНИ | |||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | ||
| 1 | 2 | 1 | 1 | 1 | |||||||||||||
| 1 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | |||||||
| 1 | 5 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | |||||
| 2 | 4 | 1 | 1 | ||||||||||||||
| 3 | 5 | 4 | 4 | 4 | 4 | 4 | |||||||||||
| 4 | 5 | 3 | 3 | 3 | 3 | 3 | 3 | ||||||||||
Если в первом случае срок выполнения всех операций составит 17 дней, то для второго случая он равен 16 дням.
Метод ветвей и границ позволяет получить оптимальный календарный план рассмотренного выше примера. Однако трудоемкость оптимизации при использовании указанного метода обуславливает невозможность его применения при распределении на сетях большой размерности и тем более на стохастических сетях в многопроектных разработках. Кроме того, для этих задач функции контроля и регулирования являются такими же значимыми, как и функция планирования. Существующие же решения этих функций не обеспечивают. Нужен принципиально новый подход.
В работе [23] ситуация, согласно которой с целью выполнения проекта за минимальное время необходимо изменить в сторону увеличения начальный срок критической операции, а не операции, имеющей резерв времени, названа парадоксом.
В чем причина возникающих парадоксов? Из рассмотренного выше примера следует, что возможны различные варианты перехода ресурсов с одной операции на другую. Так, например, на третьем шаге в первом случае (см. табл.2) на операцию (3,5) один человек переходит с операции (2,4) и три человека переходят с операции (1,3).
Во втором случае три человека с операции (1,3) переходят на выполнение операции (4,5) (см. табл.3). В том и другом случае между указанными операциями возникают связи по использованию одних и тех же ресурсов.
Для начала любой операции необходимо, чтобы к данному моменту времени были бы не только выполнены те операции, каждая из которых необходима данной согласно технологии проектирования проекта, а также свободны ресурсы, обеспечивающие ее выполнение.
Поскольку возможны различные варианты перехода каждой единицы ресурса с одной операции на другую, то задача нахождения ресурсных связей многовариантна (обусловлена переменной структурой графа). Каждый вариант распределения ресурсов определяет топологию сетевой модели, которая характеризуется своими параметрами. Оптимальный вариант определяет оптимальную топологию сетевой модели согласно выбранному критерию. Данное утверждение справедливо и для многопроектных разработок.
На рис. 2, 3 представлены сетевые графики табл. 2, 3, где между операциями установлены не только связи, обусловленные технологией проектирования проекта, но также связи по ресурсам. Соответствие операций на указанных рисунках и таблицах установлено через продолжительности выполнения работ. Критический путь на рис. 2, 3 обозначен жирной линией.
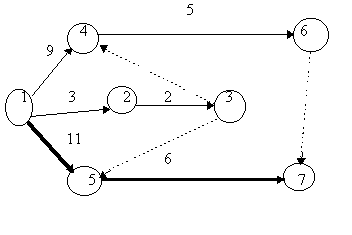
Рис.2.

Рис.3.
Введем
следующие обозначения: ![]() множество работ многопроектной
разработки (данное
множество включает работы всех проектов, которые задаются общим списком);
множество работ многопроектной
разработки (данное
множество включает работы всех проектов, которые задаются общим списком); ![]() код работы (код работы состоит из кода
проекта и кода работы в проекте),
код работы (код работы состоит из кода
проекта и кода работы в проекте), ![]()
![]() множество работ, результаты каждой из
которых необходимы для работы
множество работ, результаты каждой из
которых необходимы для работы
![]() согласно технологии и принятому порядку
ведения работ в проекте (технологические условия),
согласно технологии и принятому порядку
ведения работ в проекте (технологические условия), ![]()
![]() вид ресурса, которым может выполняться
работа
вид ресурса, которым может выполняться
работа
![]() ,
,
![]()
![]() _ число ресурсов, назначенное
на работу
_ число ресурсов, назначенное
на работу
![]()
![]() продолжительность выполнения работы
продолжительность выполнения работы
![]()
![]()
![]() трудоемкость работы
трудоемкость работы
![]() в чел/дн,
в чел/дн,
![]()
![]() множество работ (ресурсные
условия), по окончании каждой из
которых ресурсы переходят на работу
множество работ (ресурсные
условия), по окончании каждой из
которых ресурсы переходят на работу
![]() ,
,
![]() t1- время функционирования
системы.
t1- время функционирования
системы.
![]() число проектов;
число проектов;
![]() число различных видов
ресурсов, обеспечивающих выполнение многопроектной разработки;
число различных видов
ресурсов, обеспечивающих выполнение многопроектной разработки;
![]() число ресурсов l - го вида,
число ресурсов l - го вида,
![]()
![]() множество работ, выполняемых l-ым
видом ресурсов в к-ую единицу времени,
множество работ, выполняемых l-ым
видом ресурсов в к-ую единицу времени,
![]()
![]()
![]() продолжительность критического пути m-го проекта в сетевом графике без учета
ресурсов,
продолжительность критического пути m-го проекта в сетевом графике без учета
ресурсов,
![]()
![]() продолжительность самой длинной
цепочки работ, выполняемых l-ым видом
ресурсов,
продолжительность самой длинной
цепочки работ, выполняемых l-ым видом
ресурсов,
![]()
![]() весовой коэффициент работы
весовой коэффициент работы
![]()
![]() максимально возможное число
ресурсов для работы
максимально возможное число
ресурсов для работы
![]()
![]() код q-го условия для работы
код q-го условия для работы
![]()
![]()
![]() срок начала
работы
срок начала
работы
![]()
![]() срок окончания q-го условия для работы
срок окончания q-го условия для работы
![]()
![]()
|
Laboratory.Ru |
|