Метод критического пути в многопроектных разработках с учетом ресурсов

Л. П. Костина, канд. физ. - мат. наук.
 (Санкт - Петербургский государственный университет).

Страница 3

Страница 1
Страница 2
Страница 3

3. Математическая формулировка задачи, обусловленной переменной структурой графа

В свете сказанного  выше задача оптимального распределения ресурсов на сетях ( определения оптимальной структуры графа ) формулируется следующим образом   известно ( состояние системы в момент времени ).

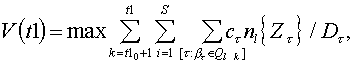для любого     (1)   

                                                                                    (2)

                                                                              (3) 

                         целое,                                                            (4)

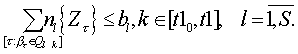                                                                       (5)

При заданном начальном состоянии системы  в момент времени   необходимо найти в области, определяемой ограничениями: (2) - (5), оптимальную траекторию движения (под оптимальной траекторией движения системы мы понимаем экстремальный ресурсный граф, параметры которого для любого   обеспечивают максимальное значение функции (1)).

В математической формулировке задачи под ресурсным графом мы понимаем сетевую модель, отображающую многопроектную разработку с учетом ресурсов, где вершинами являются работы, а дугами являются  связи между работами по ресурсам (французский вариант представления ресурсного графа "работы - связи").

Запись    обозначает  работу      включенную в ресурсный граф. Положение каждой работы в графе определяется путем указания для нее множества ресурсных условий   В качестве  параметров системы выбраны величины:   , ,  характеризующие состояние системы в каждый момент времени  (система   функционирует в дискретном времени).

Обоснованность критерия (1) следует из определения ресурсов нескладируемого вида, а также теоремы о критических путях в многопроектных разработках c учетом ресурсов. Cогласно определению нескладируемых ресурсов неэффективно использованная единица ресурса любого вида в единицу времени приводит к потери ресурса ( если оборудование простояло час или было неэффективно использовано, то эту потерю не восполнить).

Физически критерий (1) означает, что в оптимальном графе суммарный объем выполненных работ с учетом их весовых коэффициентов за любой интервал времени должен быть максимальным. Согласно ограничению (2) работы не могут начинаться раньше окончания своих условий. Данное ограничение обусловлено технологией проектирования проектов и накладывается на положение работ в графе (на структуру графа). В работах [23, 24 ] изложен алгоритм сформулированной выше задачи c доказательством получения оптимальной структуры графа для случая, когда каждая работа многопроектной разработки может выполняться с переменной интенсивностью потребления ресурсов.

Для случая выполнения работ с постоянной интенсивностью использования ресурсов на каждой работе получено приближенное решение задачи,  обеспечивающее равномерную загрузку ресурсов [25].

4. Заключение

Необходимость принципиально новой трактовки проблемы распределения ресурсов на сетях обусловлена объективно существующей закономерностью, суть которой состоит в том, что при переходе каждой единицы ресурса с одной работы на другую между этими работами возникают связи по использованию одного и того же ресурса. Поскольку возможны различные варианты указанных связей, то данная задача обусловлена переменной структурой графа. По этой причине производить расчет сетевых графиков, каждый из которых построен на основании технологии и принятой организации работ по каждому проекту нет никакого смысла. Приведенные выше примеры показывают что при таком подходе сетевая модель вообще выпадает из управления.

В любом случае модель - это система, в которой отношение между ее элементами в какой - то степени отражает другую систему - образец. Известно, что чем сложнее система, тем большее число различных состояний она может принимать. Число возможных состояний системы определяется количеством составляющих ее элементов, количеством и характером связей между ними. Как правило, модель проще образца, но она должна отражать те факторы, которые являются существенными для решения задач управления. В настоящее время при моделировании процесса управления многопроектными разработками с учетом ограниченного количества нескладируемых ресурсов не принимается во внимание существенный фактор, который состоит в том, что топология сетевой модели такой системы есть функция распределения ресурсов. Новая трактовка проблемы распределения ресурсов на сетях позволит выйти из тупика и совершить качественный скачок в области создания автоматизированных систем управления.

Литература

1. Калачев В. Н., Немчинов Б. В., Кривоножко В. Е. Задачи планирования   в гибких производственных системах. // Автоматика и телемеханика. 1995.    N6. C. 155-164.

2. Левин В. И. Оптимизация расписаний в системах с неопределенными   временами обработки. // Автоматика и телемеханика. 1995. N2. C. 99-110.

3. Шарыгин П. И. Оценки приближенного решения одной задачи    календарного планирования. // Дискретный анализ и исследование   операций. Новосибирск: Ин-т математики СО РАН, 1995, т. 2. N1, 57-67.

 4. Кононов А. В. О расписаниях работ на одной машине с длительностями  нелинейно зависящими от времени. // Дискретный анализ и исследование  операций. 1995. Т. 2, N1. C. 21-35.

5. Левин В. И. Задача трех станков с неопределенными временами  обработки. // Автоматика и телемеханика. 1996. N1. C. 109 - 120.

6. Хоботов. Л. Б. Использование оптимизационно-имитационного подхода  для решения задач  планирования и выбора маршрута обработки.  // Автоматика и телемеханика. 1996. N 1. C. 121-127.

 7. Кононов А. В. Комбинаторная сложность составления расписаний для  работ с простым линейным ростом длительностей. // Дискретный анализ и исследования операций. 1996. Т. 3, N 2. C. 15-32. 

8. Левин В. И. , Мирецкий И. Ю. Оптимальное планирование работ в  конвейерных системах. // Автоматика и телемеханика. 1996. N 6. С. 3-30.

9. Обзор исследований по вопросам оптимального использования ресурсов в системах сетевого планирования и управления, из-ние НИИСП Госстроя УССР, Киев, 1966.

10. Х. Ахьюджа. Cетевые методы управления в проектировании и  производстве.  Пер. c англ. /Под. ред. В. Н. Калашникова.  М.: Наука, 1979.

11. Cборник III-го Bcесоюзного симпозиума по проблемам планирования и  управления научными исследованиями  и разработками. М.: ЦЭМИ 1975.

12. Применение пакетов прикладных программ по экономико - математическим методам в АСУ. М.: Статистика, 1980.

13. Глушков В. М. , Михалевич В. C. и др. Управляющий этап // Управляющие системы и  машины. 1979. N3. С. 5-7.

14. Основные положения по разработке и применению систем сетевого  планирования и управления. М. , Экономика. 1974. 

15. Fersko-Weis H. Project management software // PC Magazine. 1988.  November 15. p. 178-226.

16. Fersko-Weis H. High-end project managers make the plans. // PC magazine 1989 May 16 p. 155-195.

17. Кохова С. В. Некоторые динамические задачи распределения ресурсов на сетевых графиках с переменными объемами работ. // Вестник Московского университета. сер.15. Вычислительная математика и  кибернетика. 1991. N1. C. 48-57.

18. Kouveles P., Lee H.L. Block angular structures and the loading problem in  flexible manufakcturing systems. // Oper. Res. 1991.V.39. N4. P. 666- 676.

19. Rogers V.R. White K. P. Algebraic, Mathematical Programming, and Network Models of the Deterministic Job-shop Scheduling Problem. //IEEE Trans. on Systems, Man, and Cybernetics. 1991.V. 21. N3. P. 693-697

20. Математика и кибернетика в экономике. М. , "Экономика", 1975.

21. Голенко Д. И. и др. Применение статистической оптимизации при управлении разработками в условиях неопределенности. Материалы IX Всесоюзного семинара Киев, " Наукова думка", 1974. C 72-74.

22. Костина Л. П. Причины парадоксов при распределении ресурсов на  сетях в книге Х. Ахьюджа " Сетевые методы управления в   проектировании и производстве" (под ред. В.В Калашникова. М. , 638 c).  Деп. организацией  МРС "ТТЭ". Сер.0. Вып. 18, Д05134 от   5 августа 1982 г.

23. Костина Л. П. Постановка проблемы оптимального распределения  ресурсов на стохастических сетях со сложной пространственно-
   временной структурой. // Вестник Санкт -Петербургского университета.  Сер.1. 1992.  Вып. 2 (8). С. 15-19.

24. Костина Л. П. Метод решения задачи оптимального распределения  ресурсов на стохастических сетях со сложной пространственно-  временной структурой. // Вестник Санкт-Петербургского университета.  Сер. 1. 1992.  Вып. 3 (15).

25. Костина Л. П. Опыт создания АСУ проектной организацией на базе  методов распределения ресурсов на сетях, обусловленных переменной  структурой графа. Деп. организацией МРС "ТТЭ", серия 0,  вып. 18, Д05135 от 5 августа 1982 г.