About me
Practice in Germany: About IPVS Target Setting About work
Efficient Index Structures for Spatial Event Analysis
Providing context-awareness in future applications demands for accurate information about positions of a potentially large number of mobile objects. This requires location management systems that are capable of coping with a huge amount of such highly dynamic data. To efficiently retrieve relevant information, e.g., all objects located within a certain area, these systems must utilize adequate index structures. In the past, suitable indexes have been explored for geometric representations of location information only. However, especially indoors a variety of positioning systems are solely based on symbolic identifiers. To enable region-based queries on symbolic identifiers, the spatial inclusion relations between these identifiers must be modeled within a suitable location model. In general, a model that describes the spatial inclusion relationships between locations can be interpreted as a directed acyclic graph. Each node represents a certain location and each edge represents the fact that the target location is spatially included in the source location. In location model represented as directed acyclic graph the nodes at the lowest level represent the finest granularity of locations, this means that all mobile objects registered in the model are positioned on this level.
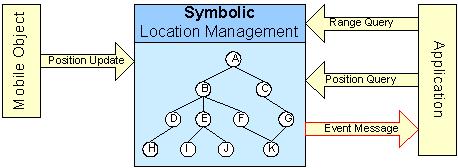
Figure 1.
Tobias Drosdol in his article "Efficient Indexing of Symbolic Location InformationŔ" represents two approaches for efficient indexing reflecting two main operations - position updates/queries and region queries. The following work considers spatial event processing based on previous research carried out in article.
An event being registered in the model should give following information: type of event (on_enter or on_leave), area (its symbolic name) and observer ID which is supposed to receive event acknowledgement. Two different types of events result creation of two maps for event storing. This storing may be realized differently. On the one hand, associating event with its area makes it logical to store event directly in the node which represents given area (below - version 2). On the other hand, as it was said above, all mobile objects are situated on the lowest level, therefore possible events will also take place on the lowest level, which provides a reason to save events only in leaves (below - version 1).
Version 1
Saving event in the nodes assumes traversing the tree down to the lowest level in order to find all children of the given area.

Figure 2.
Hence the same event has to be saved several times. The more important drawback is additional time required to traverse a tree in order to find successors. However such approach eases updates essentially. For event registration we have to compare old and new position of mobile object. Since movements happen on the lowest level and corresponding positions are saved also on the lowest level, to compare them we need no traversal upwards. If to consider the fact, that position updates take place quite often, considered approach saves time extremely. Here it is also important to remember about spatial inclusions analysis.
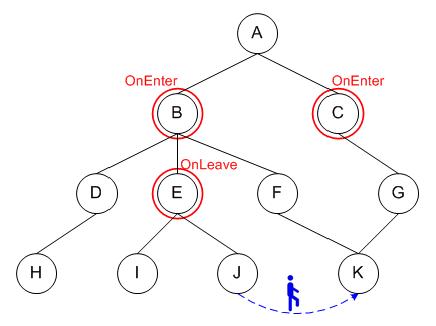
Figure 3.

Figure 4.
Version 2
Since each event is associated with a special area, it is natural to save it there directly without conducting a search for successors.

Figure 5.
In this case we avoid event registration problems of the first version (storing of the same event in several nodes and traversal in order to find leaves). However, we get new drawbacks by updates, i.e. events registration.
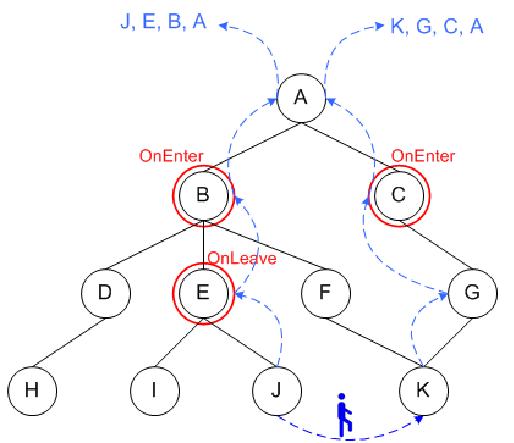
Figure 6.
Let's consider Figure 6. Mobile object moves from location J into location K. Red circles indicate nodes with registered events. Possible onEnter events may happen in node K or one of its predecessors and onLeave events - in node J or one of its predecessors. Therefore traversal of the tree is needed in order to find parents of both nodes. The search gives following results: Parents(J) = {J, E, B, A}, Parents(K) = {K, G, C, A}. On this stage spatial inclusions should be taken into account. Presence of A-node in both arrays actually means that the object did not leave and did not enter this area, i.e., no event happened. Therefore we can exclude A node, which leaves J, E, B nodes for analysis of onLeave event and K, G, C nodes for onEnter event. Final analysis denotes onLeave event in E-node and onEnter event in C-node.
Considered example shows that second version makes updates more complicated. Taking into account the fact that such updates happen much more often than event registration, if range queries take place rarely, considered approach can become too expensive.
Another possibility is a combination of both variants, i.e., use of a threshold dividing existing model on two parts, one of which would be considered as the first version and another one - as the second.