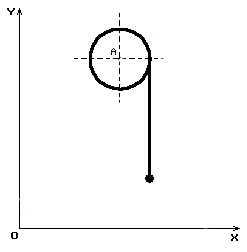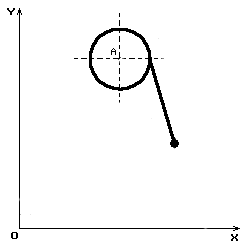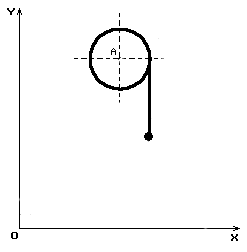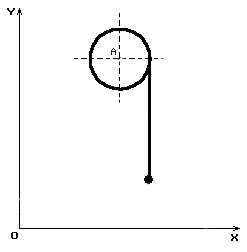Введение

 

Невозможно переоценить значимость подъемно-транспортного оборудования в современном мире. Высокие темпы производства, строительства, складирования, монтажа являются определяющими для предприятий при работе в условиях рыночной экономики. Существует  огромное количество сфер человеческой деятельности, в которых используется подъемно-транспортное оборудование или же существование которых было бы не возможно без его использования.

Подъемно-транспортные машины,  в которых используется подвижная грузовая каретка, отличаются тем, что грузовая каретка в общем случае совершает двухмерное движение в горизонтальной плоскости. В связи с этим концевой груз кроме перемещения в вертикальном направлении также перемещается в поперечных направлениях.

 

1. Актуальность темы

Подъемные машины являются типовым оборудованием производственных и металлургических цехов, закрытых и открытых складов, портов, перегрузочных станций и используются для: перемещения разнообразных твердых и сыпучих грузов; перегрузки угля, руды и других полезных ископаемых; сборочных и ремонтных работ; монтажа сборных промышленных и гражданских сооружений, оборудования; обслуживания строительных и гидротехнических работ и многого другого.

Ввиду отсутствия направляющих проводников, в подъемно-транспортных машинах грузозахватные устройства и груз при подъеме или спуске ничем не удерживается от поперечных перемещений, то есть имеют возможность кроме перемещения в вертикальном направлении, перемещаться в поперечном направлении. Разумеется, что произвольные перемещения грузозахватныхх устройств и груза в поперечном направлении не могут быть полезными т.к. они доставляют в эксплуатации дополнительные заботы в части обеспечения безопасности обслуживающего персонала и сохранности окружающих построек, следовательно необходимо каким бы то ни было способом их  полностью избегать, или же если это не возможно, минимизировать их влияния.

В современных условиях четкая и безупречная работа подъемно-транспортного оборудования на оптимальном уровне, непосредственно влияет на экономические показатели эффективности работы предприятия. В связи с этим, исследование процессов происходящих в подъемно-транспортных машинах является вполне актуальной задачей, как для сегодняшнего дня, так и для ближайшего будущего.

2.Получение уравнений динамического состояния

2.1 Начальные условия

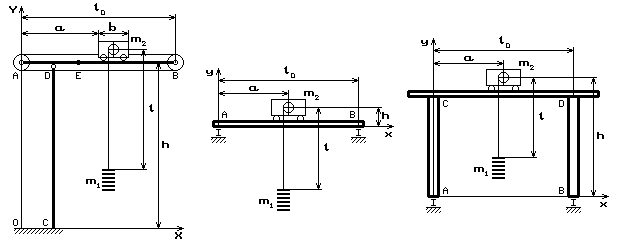
 К кранам с подвижной кареткой относятся башенные, мостовые и козловые краны, которые схематически изображены на рис. 1.

 

Рис. 1. Схемы башенного, мостового и козлового кранов

        

Рассмотрим простейший вариант подъема груза в такого рода кранах, когда каретка совершает одномерное движение при отсутствии перемещения самого крана.  Расчетная схематизация такого процесса показана на рис. 2.

Здесь изображены положения поднимаемого груза в двух состояниях – в начальном, когда длина отвеса каната равна , и в некотором текущем, когда барабан лебедки повернулся на угол  против часовой стрелки, отвес каната образовал с вертикалью угол , отсчитываемый также против часовой стрелки, а его длина стала равной .

Координаты груза в его текущем состоянии обозначим посредством символов  и .

 

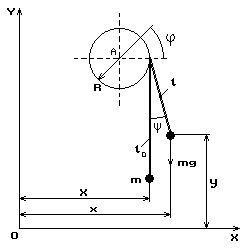
Рис. 2. Схема подъема груза при горизонтальном перемещении каретки

 

В этом текущем состоянии каретка переместилась таким образом, что точка набегания каната на барабан приобрела координату  в принятой системе отсчета . Можно считать, что  является также и текущей горизонтальной координатой каретки, отсчитываемой от ее некоторого первоначального положения (на рис.1 эта координата обозначена символом ).

 

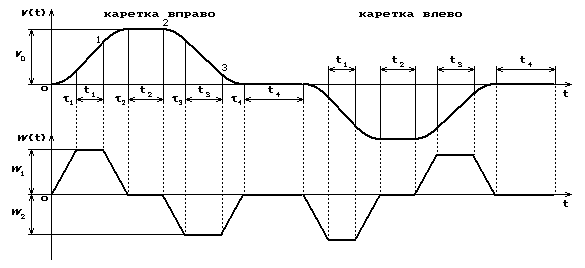
Рис. 3. Изменение скорости и ускорений каретки при ее горизонтальном перемещении

 

Будем полагать, что перемещение каретки задано, и при этом ее скорость  и ускорение  изменяются, например, так, как показано на рис. 3.

2.2 Получение уравнений динамического состояния

 

С помощью схемы, приведенной на рис. 2, запишем текущие координаты груза в форме

,

где , как было сказано выше, заданная координата грузовой тележки, начальная длина отвеса каната,  текущая его длина,  угол, образуемый отвесом подъемного каната с вертикалью. С помощью (1) находим

.                  

С использованием соотношений (2) квадрат скорости груза определится в форме

,

и тогда кинетическую энергию в целом всей системы найдем как

,             

где  текущий угол поворота барабана;  момент инерции барабана (здесь считается этот параметр постоянным, то есть пренебрегается его изменением за счет присоединенной массы навиваемого на барабан каната);  масса концевого груза.

 

Потенциальная энергия системы представится в форме

.

 

 

Функция Лагранжа  будет иметь вид

                            

Проведя упрощения в результате таких  окончательно получим вместо

,

что несколько упрощает процедуру построения уравнений движения.

Теперь вычислим частные производные от функции Лагранжа по обобщенным координатам.

В результате после  упрощения уравнения динамического состояния рассматриваемой системы будут иметь такой вид

          

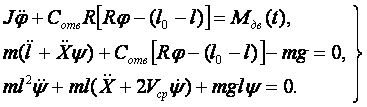
Вывод

 

Решение системы полученной системы позволяет определить максимальные поперечные перемещения груза при любом заданном законе перемещения каретки , максимальные динамические усилия в подъемном канате при различном характере изменения движущего момента  и др.

 

Список литературы

1. Антовиль А. М. «Теория механизмов и машин». Высшая школа. М., 1961 г.

2. Сергеев В.П. Строительные машины и оборудование. М.: “Высшая школа”, 1987 г.

3. Ландау Л.Д., Лифшиц Е.М., Механика- М.: Наука, 1973 г.