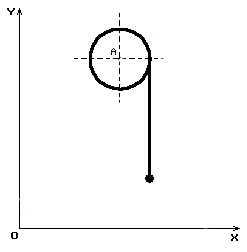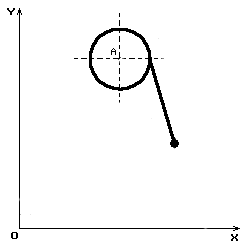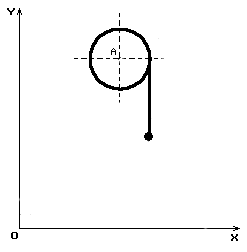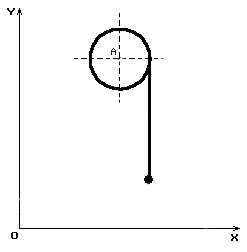Вступ

 

Неможливо переоцінити значення підйомно-транспортного устаткування в сучасному світі. Високі темпи виробництва, будівництва,
складування, монтажу є визначаючими для підприємств при роботі в умовах ринкової економіки. Існує величезна кількість сфер людської діяльності, в яких використовується підйомно-транспортне устаткування або ж існування
яких би не було можливе без його використовування.

Підйомно-транспортні машини, в яких використовується рухома вантажна каретка, відрізняються тим, що вантажна каретка в загальному
випадку скоює двомірний рух в горизонтальній площині. У зв'язку з цим кінцевий вантаж окрім переміщення у вертикальному напрямі також переміщається в поперечних напрямах.

.

 

1. Актуальність теми

Підйомні машини є типовим устаткуванням виробничих і металургійних цехів, закритих і відкритих складів, портів, перевантажувальних
станцій і використовуються для: переміщення різноманітних твердих і сипких вантажів; перевантаження вугілля руді і інших корисних копалин; складальних і ремонтних робіт; монтажу збірних промислових і цивільних споруд, устаткування;
обслуговування будівельних і гідротехнічних робіт і багато чого іншого.

Зважаючи на відсутність направляючих провідників, в підйомно-транспортних машинах вантажозахватні пристрої і вантаж при підйомі
або спуску нічим не утримується від поперечних переміщень, тобто мають нагоду окрім переміщення у вертикальному напрямі переміщатися в поперечному напрямі. Зрозуміло, що довільні переміщення грузозахватныхх пристроїв і вантажу в поперечному
напрямі не можуть бути корисними оскільки вони доставляють в експлуатації додаткові турботи в частині забезпечення безпеки обслуговуючого персоналу і збереження навколишніх
споруд, отже необхідно яким би то ні було способом їх повністю уникати, або ж якщо це не можливо мінімізувати їх впливи.

В сучасних умовах чітка і бездоганна робота підйомно-транспортного устаткування на оптимальному рівні, безпосередньо впливає
на економічні показники ефективності роботи підприємства. У зв'язку з цим дослідження процесів відбуваються в підйомно-транспортних машинах є цілком актуальною задачею, як для сьогоднішнього дня,
так і для найближчого майбутнього.

2.Отримання рівнянь динамічного стану

2.1 Початкові умови

 

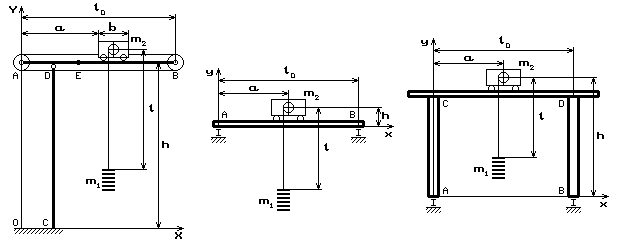
 До кранів з рухомою кареткою відносяться баштові, мостові і козлові крани, які схематично зображені на мал. 1.

 

Мал. 1. Схеми баштового, мостового і козлового кранів

        

Розглянемо найпростіший варіант підйому вантажу в такого роду кранах, коли каретка скоює одновимірний рух за відсутності
переміщення самого крана. Розрахункова схематизація такого процесу показана на мал. 2.

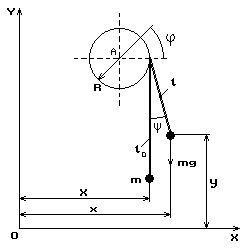
Тут зображені положення вантажу, що піднімається, в двох станах – в початковому, коли довжина схилу каната рівна , і в деякому поточному, коли барабан лебідки обернувся на кут проти годинникової стрілки, схил каната утворив з вертикаллю кут , відлічуваний також проти годинникової стрілки, а його довжина стала рівною .

Координати вантажу в його поточному стані позначимо за допомогою символів _і  .

 

Мал. 2. Схема підйому вантажу при горизонтальному переміщенні каретки

 

В цьому поточному стані каретка перемістилася таким чином, що точка набігання каната на барабан придбала координату   в прийнятій системі відліку . Можна вважати, що  також і поточною горизонтальною координатою каретки відлічуваної від її деякого первинного положення (на мал.1 ця координата позначена символом ).

 

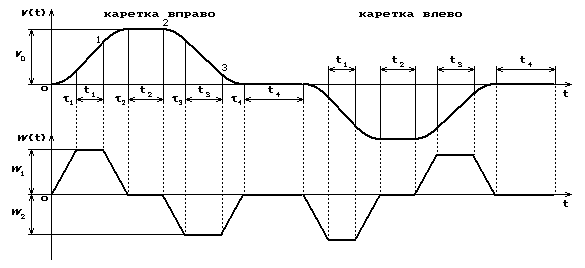
Мал. 3. Зміна швидкості і прискорень каретки при її горизонтальному переміщенні

 

Вважатимемо, що переміщення каретки задано, і при цьому її швидкість  і прискорення   змінюються, наприклад, так, як показано на мал. 3.
.

2.2 Отримання рівнянь динамічного стану

 

За допомогою схеми, приведеної на мал. 2, запишемо поточні координати вантажу у формі

,

де , як було сказане вище, задана координата вантажного візка, початкова довжина схилу каната,  поточна його довжина,  кут,
утворюваний схилом підйомного каната з вертикаллю. За допомогою (1) знаходимо

.                  

З використанням співвідношень (2) квадрат швидкості вантажу визначиться у формі

,

і тоді кінетичну енергію в цілому всієї системи знайдемо як

,             

де  поточний кут повороту барабана; момент інерції барабана ;  маса кінцевого вантажу.

 

Потенційна енергія системи представиться у формі

.

 

 

Функція Лагранжа  матиме вигляд

                            

Провівши спрощення в результаті таких остаточно отримаємо

,

що дещо спрощує процедуру побудови рівнянь рух..

Тепер обчислимо приватні похідні від функції Лагранжа по узагальнених координатах.

В результаті після спрощення рівняння динамічного стану даної системи матимуть такий вигляд

          

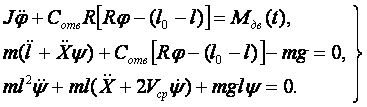
Висновок

 

Рішення системи отриманої системи дозволяє визначити максимальні поперечні переміщення вантажу при будь-якому заданому
законі переміщення каретки, максимальні динамічні зусилля в підйомному канаті при різному характері зміни рушійного моменту і ін.

 

Література

1. Антовиль А. М. «Теория механизмов и машин». Высшая школа. М., 1961 г.

2. Сергеев В.П. Строительные машины и оборудование. М.: “Высшая школа”, 1987 г.

3. Ландау Л.Д., Лифшиц Е.М., Механика- М.: Наука, 1973 г.