Содержание |
Актуальность проводимого исследования |
Широкое распространение радиоэлектронных устройств с применением цифровой обработки сигналов обуславливает повышенный интерес к вопросам диагностирования их технического состояния. Одной из разновидностей диагностирования цифровых узлов и блоков является тестовое диагностирование, применение которого на этапе проектирования и изготовления цифровых узлов позволяет определить правильность их функционирования и осуществить процедуру поиска неисправностей. При разработке тестовой диагностики возникает сложность в определении эталонных реакций при тестировании существующих схем, в определении оптимального числа контрольных точек для снятия выходной реакции диагностируемой цифровой схемы. Это можно сделать либо создавая прототип разрабатываемого цифрового устройства и проводя его диагностику аппаратурными методами, либо осуществляя моделирование на ЭВМ как цифрового устройства, так и процесса диагностики. Наиболее рациональным является второй подход, который предполагает создание автоматизированных систем диагностики [5], позволяющих производить диагностику цифровых схем на стадии проектирования и способных решать следующие задачи:
-
Производить логическое моделирование цифровых схем с помощью ЭВМ. Цель логического моделирования состоит в том, чтобы выполнить функцию проектируемой схемы без её физической реализации. Проверка на правильность моделирования может быть различной в зависимости от уровня представления цифровой схемы в ЭВМ. Если, например, осуществляется проверка только значений логической функции на выходе схемы, то достаточно представить схему на уровне логических элементов [4]. Для того чтобы проверить состояния сигналов в схеме, необходимо точно описать задержки срабатывания всех элементов в условиях синхронизации[3].
-
Моделирование неисправностей. Задача обнаружения неисправностей в цифровых схемах состоит в том, чтобы определить, обладает ли цифровая схема требуемым поведением. Для решения этой задачи необходимо, прежде всего, установить модель цифровой схемы как объекта контроля, затем метод обнаружения неисправностей и, наконец, модель неисправностей. С точки зрения особенностей поведения цифровых схем их можно разделить на комбинационные и последовательностные. В отношении обнаружения неисправностей комбинационные схемы являются сравнительно простой моделью. Последовательностные схемы в отношении поведения характеризуются наличием внутренних контуров обратной связи, поэтому обнаружение неисправностей в них в общем случае чрезвычайно затруднено.
-
Моделирование процесса тестовой диагностики. Классическая стратегия тестирования цифровых схем основана на формировании тестовых последовательностей, позволяющих обнаруживать заданные множества их неисправностей. Для реализации генератора тестовой последовательности желательно использовать простейшие методы, позволяющие избежать сложной процедуры их синтеза. К ним относятся следующие алгоритмы:
- формирование всевозможных входных тестовых наборов, т.е. полного перебора двоичных комбинаций. В результате применения подобного алгоритма генерируются счётчиковые последовательности;
- формирование случайных тестовых наборов с требуемыми вероятностями единичного и нулевого символов по каждому входу цифровой схемы;
- формирование псевдослучайных тестовых последовательностей;
Основным свойством распространённых алгоритмов формирования тестовых последовательностей является то, что в результате их применения воспроизводятся последовательности очень большой длины. Поэтому на выходах проверяемой цифровой схемы формируются её реакции, имеющие ту же длину [6]. Естественно возникают проблемы их запоминания и хранения. Простейшим решением, позволяющим значительно сократить объём хранимой информации об эталонных выходных реакциях, является получение интегральных оценок, имеющих меньшую размерность. Для этого используются алгоритмы сжатия информации. Для того чтобы применять метод компактного сжатия тестирования, необходимо рационально выбирать алгоритм формирования тестовых последовательностей и метод сжатия информации.[2] Для диагностики любой комбинационной схемы особый интерес представляет сигнатурный анализатор, в основе построения которого лежит алгоритм сжатия информации — сигнатурный анализ.
-
Анализ методов оценки эффективности компактного тестирования. Построение сложных цифровых устройств требует повышенного внимания к компактным методам тестирования для каждого конкретного применения. Поэтому возникает необходимость в оценке эффективности того или иного метода компактного тестирования. В настоящее время в литературе рассматриваются способы сравнения методов компактного тестирования.
Основные понятия сигнатурного анализа |
В настоящее время в новой технике тестирования цифровых схем сигнатурный анализ применяется наиболее часто. Это было предопределено несколькими причинами [5], например такими: равномерность закона распределения вероятности Pi необнаружения ошибки кратности i и множество необнаруживаемых ошибок Vi кратности i включает в себя маловероятные конфигурации ошибочных бит в последовательности данных. Построить сигнатурный анализатор можно двумя способами:
- метод деления полиномов;
- метод свёртки;
Главная идея сигнатурного анализа при использовании метода деления полинома на полином основывается на выполнении операции деления многочленов. В качестве делимого используется поток данных, формируемых на выходе анализируемого цифрового узла, который может быть представлен как многочлен p(x) степени L-1, где L — длина потока. Делителем служит примитивный неприводимый полином p(x), в результате деления на который получается частное q(x) и остаток S(x), связанные соотношением
| p(x)= q(x) p(x)+ s(x), |
где остаток s(x), представляющий собой полином степени, меньшей чем m=degP(x), называется сигнатурой [9]. Приведем схему сигнатурного анализа на примере полинома x5+x4+x2+1
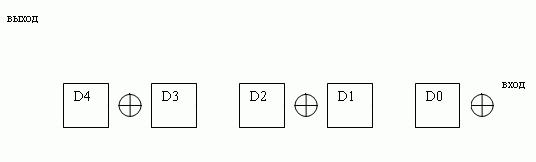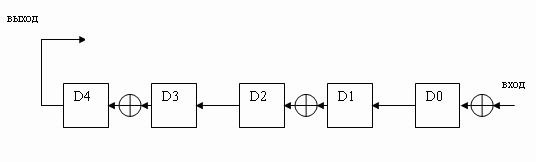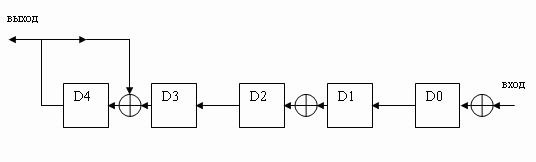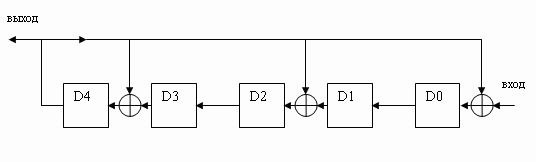 |
| Рисунок 1 — Cхема сигнатурного анализатора, построенного по методу деления полиномов. |

|
| Рисунок 2 — Cхема сигнатурного анализатора, построенного по методу свертки. |
Какие изделия пригодны для испытания методом сигнатурного анализа |
Как
правило, в изделия, при эксплуатации которых предполагается использовать
сигнатурный анализ, в процессе разработки вносят определенные средства,
позволяющие производить этот анализ наиболее простыми и дешевыми приборами
и повысить эффективность контроля. Прежде всего это средства, позволяющие
разрывать в режиме контроля цепи обратной связи в контролируемой схеме
[7]. Когда выходит из строя один из элементов, входящих в контур с
обратной связью, локализовать неисправности внутри этого контура с помощью
сигнатурного анализа не
удается.
На практике,
как правило, не требуется разрывать контуры с обратной связью, включающие
в себе всего несколько простейших логических элементов, так как
локализация сигнатурным анализом неисправности с точностью до такого
контура позволяет быстро выявить неисправность конкретного элемента
другими методами. Что же касается МПС в целом, то она целиком охвачена
обратной связью по контуру программного управления.
Поэтому для применения
сигнатурного анализа необходимо иметь возможность разрывать цепи обратной
связи в режиме тестирования МПС. Для однокристального микропроцессора это
условие реализуется отключением шины данных от входа МП. Разрыв обратной
связи по шине данных можно реализовать с помощью механических
переключателей или электронных ключей.
Вторым важным условием
пригодности МПС для испытаний с помощью сигнатурного анализа является
наличие схем, вырабатывающих сигналы Пуск и Стоп, необходимые сигнатурному
анализатору для выработки измерительного "окна" [8], т.е. интервала
времени, в течении которого накапливается сигнатура.
Третьим требованием
является наличие в составе МПС ПЗУ, в котором содержится тестовая
программа. В качестве тестовой может выступать как специально
разработанная, так и определенная рабочая программа, если она, по мнению
разработчика, в достаточной мере использует все устройства МПС.
Увеличение объема
аппаратуры и стоимости разработки МПС с учетом требований применимости
сигнатурного анализа по сравнению с объемом и стоимостью обычной МПС не
превышает в среднем 1%.
Многоканальный сигнатурный анализатор |
Предположим, что одноканальный анализатор используется для анализа цифрового узла, имеющего каналов, причём выходных последовательностей в данном случае преобразуются в одну последовательность вида
 |
| где |
 |
- значение двоичного символа на -м выходе цифрового узла в -й такт его работы, а тактовая частота работы анализатора в раз выше частоты синхронизации исследуемого узла. При этом в каждый такт работы анализатора на его вход последовательно, начиная с первого выхода, поступают значения |
 |
Функционирование одноканального анализатора в многоканальном режиме, когда количество каналов равняется , описывается системой уравнений |
 |
где численное значение коэффициентов определяется на основании следующей системы уравнений |
 |
Коэффициенты |
 |
определятся следующим образом: |
 |
Мера качества сигнатурных анализаторов |
Анализу
качества сигнатурных анализаторов(СА) посвящено много работ. Хотя в
результате этих исследований не выработана единая мера качества,
предпочтение отдается СА, описываемым неприводимыми примитивными
полиномами. В моей работе за меру качества взята сумма минимальных
расстояний полиномиальных кодов, порождаемых полиномом и переменной
длинной анализируемой последовательности. Предлагаемая мера позволяет
также сравнивать между собой примитивные
СА.
СА можно
рассматривать как линейную последовательную машину без выходов,
определяемую в виде совокупности двух объектов C=(A,B) [1]. Для вычисления
суммы длин минимальных расстояний полинома степени r выполняем следующие
действия:
- Строим бинарную (r,r) матрицу A:
0 0 0 ... 0 a0 1 0 0 ... 0 a1 0 1 0 ... 0 a2 0 0 1 ... 0 a3 ............................ 0 0 0 ... 1 ar-1 - Строим вектор-столбец B размерности r, у которого первая компонента равна 1, а остальные являются нулями.
- Строим бинарную (r,n)-матрицу Hc(n) = [Ak-1B, Ak-2B ... A1B, A0B]. В операции умножения бинарных матриц под умножением бинарных элементов понимаем их конъюнкцию, а под сложением сложение по модулю 2.
- Обозначим минимальное расстояние dc(n), где n — длина входной последовательности. СА обнаруживает dc-1 ошибок. Если полином примитивный, то для n=2r dc(n)=2.
- Допустим, что для n, которое больше r dc(n)=d [1]. Если матрица А неособенная (это будет тогда и только тогда, когда a0=1), то для вычисления dc(n+1) нужно проверить, существуют ли такие наименьшие d' меньше d-2 и n-1 больше k1...kd' и больше нуля, что AnB можно получить линейной комбинацией из d' столбцов из матрицы H, которые расположены после n-того столбца. Если такое d' существует, то dc(n+1)=d'+2, иначе dc (n+1)=dc(n)=d.
- Суммируем длины всех минимальных расстояний, полученных при длинах входных последовательностях от 1 до 2r-1, где r — старшая степень полинома.
Для примера рассмотрим 4 сигнатурных анализатора, которые описываются не делящимися на x полиномами 16-й степени:
| Полином | Сумма длин минимальных расстояний |
| C1: непримитивный полином pc1=x16+x15+x12+x7+x6+x5+x4+1 | 131128 |
| C2: примитивный полином pc2=x16+x12+x12+x9+x7+1 | 197094 |
| C3: примитивный полином pc3=x16+x15+x13+x12+x11+x10+x9+ x8+x7+x6+x5+x3+x+1 | 197290 |
| C4: примитивный полином
pc4=x16+x13+x12+x11+x7+x6+x3+x+1
|
196771 |
| Таблица 1 — Сумма длин минимальных расстояний. |
Таким образом, мера качества непримитивного СА С1 значительно ниже мер примитивных СА. СА С3 оказался лучше, чем СA С2, а СА С4 хуже.
Заключение |
Основным
свойством распространённых алгоритмов формирования тестовых
последовательностей является то, что в результате их применения
воспроизводятся последовательности очень большой длины. Поэтому на выходах
проверяемой цифровой схемы формируются её реакции, имеющие ту же длину.
Естественно возникают проблемы их запоминания и хранения. Простейшим
решением, позволяющим значительно сократить объём хранимой информации об
эталонных выходных реакциях, является получение интегральных оценок,
имеющих меньшую размерность. Для этого используются алгоритмы сжатия
информации.
Для того
чтобы применять метод компактного сжатия тестирования, необходимо
рационально выбирать алгоритм формирования тестовых последовательностей и
метод сжатия информации.
Литература |
- Барашко А.С. Об одной мере качества сигнатурных анализаторов. Отдельный оттиск — Рига: Зинатне, 1988.
- Уильямс Г.Б. Отладка микропроцессорных систем: Пер. с англ. — М.: Энергоатомиздат, 1988.
- Микропроцессоры: системы программирования и отладки / В.А.Мясников, М.Б.Игнатьев, А.А.Кочкин, Ю.Е.Шейнин; Под ред. В.А.Мясникова, М.Б.Игнатьева. — М.: Энергоатомиздат, 1985.
- Фергусон Дж., Макари Л., Уилльямз П. Обслуживание микропроцессорных систем: Пер. с англ.- М.: Мир, 1989.
- Кирьянов К.Г., Соловейчик Э.Б. К проэктированию РЭА, ориентированной на диагностику сигнатурным анализом. — Техника средств связи. Сер. Радиоизмерительная техника, 1980, вып. 1 (26), с 9 — 84.
- Пухальский Г.И., Новосельцева Т.Я. Цифровые устройства: Учебное пособие для втузов.- СПб.: Политехника, 1996.
- Гилл А. Линейные последовательные машины. — М.:Наука, 1974. — 288 с.
- Питерсон У, Уелдон Э. Коды, исправляющие ошибки. — М.:Мир, 1976 — 400 с.
- Smith J. E. Measures of the effectiveness of fault signature analysis //IEEE Trans. on Comput. — 1980. — Vol. C-29, N 6. — P.510-514
| в начало |