Реализация микропрограммного устройства управления композицией автоматов с жесткой и программируемой логикой.

Баркалов А.А., Матвиенко А.В.

 

Баркалов А.А., Матвиенко А.В. Реализация микропрограммного устройства управления  композицией  автоматов  с  жесткой  и программируемой логикой // Микропроцессорные средства, разработка и применение. – К.: ИК АН УССР, 1985. – С. 38-40.

 

7.1. Принцип функционирования автоматов на счетчиках

 

Если исходная ГСА является линейной, то есть не менее 75% вершин  составляют операторные вершины, то оптимизация аппаратурных затрат возможна за счет замены регистра памяти счетчиком [9]. Введем ряд определений, во многом аналогичным определениям для композиционных микропрограммных устройств управления.

Определение 7.1. Линейной последовательностью состояний (ЛПС) ГСА Г называется конечный кортеж a_g =<a_g1,.. a_gFg>, такой, что для любой пары состояний a_gi, a_gi+1Î A, где i – номер компоненты кортежа a_g, существует переход <a_gi, a_gi+1> автомата,  интерпретирующего ГСА Г.

Определение 7.2. Состояние a_m Î A^g, где A^g Í A – множество состояний, входящих в кортеж a_g, называется входом ЛПС a_g, если существует переход <a_s, a_m>, где a_s Ï A^g либо a_s Î A^g и соответствует компоненте с большим номером, чем a_m.

Определение 7.3. Состояние a_m Î A^g, называется главным входом ЛПС a_g, если    a_m – начальное состояние автомата, или  a_m – вход ЛПС a_g, переход в который определяется последовательностью логических условий, в которой последний компонент равен нулю.

Определение 7.4. Состояние a_m Î A^g, называется выходом ЛПС a_g, если существует безусловный переход  <a_m, a_s>, где a_s Ï A^g , либо выход вершины, отмеченной состоянием a_m, связан с входом условной вершины.

Пусть для ГСА Г получено множество ЛПС a(Г)={a₁, …, a_G}, определяющее разбиение П_А множества состояний автомата на классы эквивалентности A¹, …, A^G, и пусть для каждой ЛПС выполнено такое кодирование состояний, что если <a_gi, a_gi+1> входит в ЛПС a_g Î a(Г), то

                                    K(a_gi+1)=K(a_gi)+1.                                    (7.1)

 Условие (7.1) идентично условию естественной адресации микрокоманд в КМУУ.

В этом случае регистр памяти автомата может быть заменен счетчиком (Рис.7.1).  Назовем автоматы со счетчиками С-автоматами (от слова “counter”).

 

 

 

 

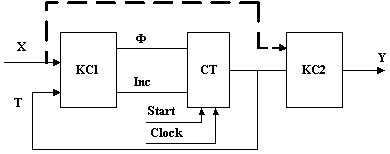
Рис.7.1. Структурная схема С-автомата

 

С-автомат функционирует следующим образом. По сигналу Start в счетчик  СТ записывается нулевой код, соответствующий начальному состоянию а₁ Î A. В момент времени t в СТ находится код  K(a_m) состояния a_m Î A^g. Если а_m не является выходом ЛПС a_g, то схема КС₁ формирует сигнал Inc и по сигналу Clock к содержимому СТ прибавляется единица, тем самым согласно (7.1) происходит переход в следующее состояние ЛПС a_g. Если a_m является выходом ЛПС a_g, то сигнал Inc не формируется и схема КС₁ формирует функции Ф=Ф(Т,Х), вызывающие переход в состояние а_s Î A, код которого определяется не в соответствии с (7.1). В каждом цикле схема КС₂ формирует выходные сигналы Y=Y(T,X) для модели Мили либо Y=Y(T) для модели Мура. Функционирование прекращается после перехода автомата в состояние а₁.

Метод синтеза С-автомата включает следующие этапы:

1.       Формирование минимального разбиения множества состояний А на классы, соответствующие ЛПС a_g исходной ГСА. Минимальное разбиение П_А={A₁,…A_G} определяется условием (7.2):

Aⁱ  Ç A^j = Æ ( i ¹ j, i, j Î {1,…,G} );

A¹ È A² È … È A^G = A;                                                                      (7.2)

A^g ¹ Æ ( g Î {1,…,G} );

G à min.

2.       Оптимальное кодирование состояний согласно (7.1)

3.       Формирование ПСТ С– автомата

4.       Реализация схем КС₁ и КC₂ в заданном элементном базисе.

Методы решения каждой из этих задач зависит от типа реализуемого автомата.

 

В начало