Шапиро М.И., Дегтярев А.А.

Профилактика кишечных инфекций в крупном городе. - Л.: Медицина,1990. - 256 с.

В книге обобщен опыт работы санитарно-эпидемиологической службы по совершенствованию профилактики кишечных инфекций с позиций теоретических, методических и организационных принципов современной эпидемиологии.

Часть 2. Эпидемиологический надзор в системе профилактики кишечных инфекций

Глава 6. Анализ многолетней динамики заболеваемости

Цель данного раздела ретроспективного анализа состоит в дифференцированной оценке характера многолетней тенденции заболеваемости, периодических ее колебаний и нерегулярных эпизодических вариаций.

По современным представлениям характер тенденции заболеваемости зависит прежде всего от качества и эффективности профилактических мероприятий, направленных на основные причины и условия развития эпидемического процесса. При дизентерии и других кишечных инфекциях - это мероприятия, которые изменяют условия передачи возбудителей через пищу и воду. Их качество и эффективность связаны с результативностью осуществления социально-экономических программ по обеспечению необходимого санитарно-гигиенического и санитарно-технического уровня производства пищевых продуктов, организации питания, водоснабжения, очистки территории и обеззараживания сточных вод, санитарного уровня населения и санитарно-гигиенических условий содержания организованных дошкольников.

Так, в связи с несовершенством технологии переработки мяса птицы среди городского населения с начала 80-х годов выявились тенденции к росту заболеваемости сальмонеллезами, кишечным иерсиниозом, кампилобактериозом. М. С. Исаева и соавт. (1981) выявили рост заболеваемости дизентерией и другими острыми кишечными инфекциями в 70-е годы в ряде северо-западных районов РСФСР. Этот рост был связан с изменениями социально-экономических условий жизни и деятельности населения. В частности, увеличение концентрации населения в районных центрах и поселках городского типа существенно опережало темпы осуществления мероприятий по развитию и совершенствованию систем водоснабжения, производства продуктов питания и улучшению санитарно-гигиенических условий в дошкольных детских учреждениях.

Кроме того, в крупных городах, на формирование тенденции заболеваемости может повлиять все нарастающее проэпидемичивание населения в связи с активной циркуляцией возбудителя, которая поддерживается сохранением достаточных санитарно-гигиенических условий для реализации механизма передачи инфекции.

Второй закономерной формой проявления эпидемического процесса при кишечных инфекциях являются многолетние периодические колебании уровня заболеваемости. Рациональное объяснение механизмов развития периодических колебаний заболеваемости может быть получено на основе теории саморегуляции. Периодичность - это естественная форма фазового развития эпидемического процесса. На ее конкретные проявления влияет совокупность природных и социальных условий, действие которых опосредуется через механизмы взаимодействия популяций возбудителя и хозяина в паразитарной экосистеме.

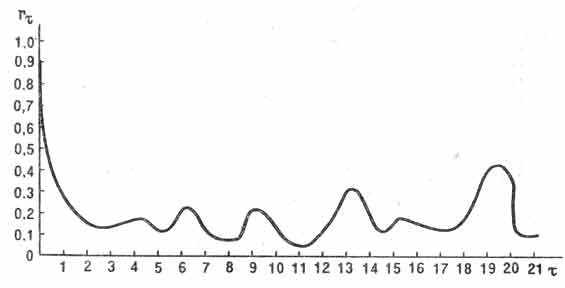
Проявления периодичности эпидемий дизентерии Зонне с течением времени существенно меняются. До середины 70-х годов основными были эпидемические циклы длительностью в 4, 6, 9, 13 и 19 лет. Это подтверждается и результатами автокорреляционного анализа (рис. 1). Но в последующий период произошли отчетливые изменения периодичности эпидемий и с 1975 г. установился двухлетний цикл. Он настолько однозначен, что нет необходимости такой вывод подкреплять статистическими оценками (при лаге в 2 года коэффициент автокорреляции в 1975—1984 гг. составлял 0,932). Как было показано в гл. 3, двухлетняя периодичность заболеваемости соответствует чередованию «жарких» и «холодных» летних периодов, т. е. в основном отражает ритм природно-климатических условий.

Рис. 1. Автокорреляционная функция динамики заболеваемости дизентерией Зонне населения Ленинграда за 1953—1987 гг. Лаг (т) выражен в годах.

В колебаниях солнечной активности выявляются многообразные волны. Первая статистически значимая периодика в колебаниях, например, суммы среднесуточных температур воздуха в летние месяцы составляет 2 года (рис. 2). Колебания солнечной активности влияют на ритм в изменениях направленности и силы действия других космо-теллурических факторов. Их совокупное влияние на эпидемический процесс при кишечных инфекциях реализуется через изменения резистентности организма, особенно в весенне-летний период при запуске сезонного подъема, возможно, через усиление вирулентности возбудителя, а кроме того, за счет активизации механизма передачи возбудителя в летние месяцы.

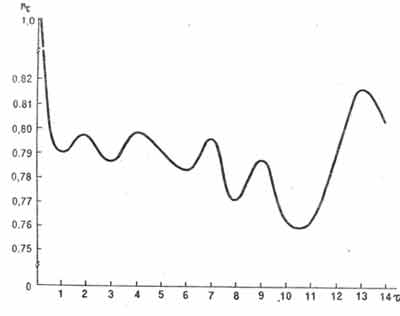
Рис. 2. Автокорреляционная функция динамики колебаний показателей суммы среднесуточных температур воздуха для района Ленинграда. Лаг (т) выражен в годах.

Анализ периодических колебаний заболеваемости необходим для решения нескольких задач. Устойчивость периодической компоненты и амплитуда колебаний являются дополнительными критериями управляемости эпидемического процесса, т. е. эффективности принятой системы профилактики. В сочетании с теоретической линией тенденции оценка периодической компоненты может быть использована для ориентировочного прогнозирования заболеваемости на предстоящие годы.

Методы анализа многолетней динамики заболеваемости

Массив исходной информации для анализа многолетней динамики формируется из данных оперативного учета заболеваемости после их коррекции по окончательным диагнозам.

При подготовке данных к обработке из них исключают заболеваемость за периоды эпизодических вспышек с установленными причинами. При анализе многолетней динамики заболеваемости кишечными инфекциями минимальная протяженность изучаемого периода определена в 10 лет.

Теоретическая линия тенденции строится по методу наименьших квадратов. Подбор функции для выравнивания ряда основывается на показателях остаточной дисперсии ( ), адекватности описания эмпирического ряда по уравнению функции ( ) и статистической значимости параметров полученных уравнений (по F-критерию Фишера и критерию Стьюдента). Все эти методы подробно описаны и литературе по математической статистике [Anderson Т., 1976]. Пригодные для эпидемиологического анализа программы апроксимации эмпирических рядов по набору функций и выбору наилучшего описания являются обычным элементом библиотек программ для ЭВМ. В программах, которые используются для этих целей нами, предпочтение отдано простейшим, в большинстве своем легко линеаризуемым функциям. Примерный набор таких функций приведен в табл. 1. Из более сложных для интерпретации криволинейных функций, не поддающихся линеаризации, мы включили в число уравнений для апроксимации рядов динамики заболеваемости кишечными инфекциями параболу II и III степени.

Таблица 1

Уравнения функций, пригодных для выравнивания эмпирических рядов динамики заболеваемости по методу наименьших квадратов

Вид функции	Вид функции

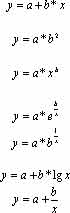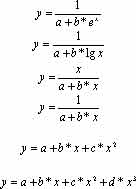При выборе функции для описания тенденции ряда показателей желательно опираться на логические представления о характере связи между изменениями уровня заболеваемости и изменениями активности определяющих его факторов. Для этого необходимо располагать данными о том, как на протяжении анализируемого периода изменялись набор мероприятий и показатели качества проведения основных потенциально эффективных профилактических мероприятий. Применительно к кишечным инфекциям это, прежде всего, данные об используемой технологии в системе производства продуктов питания, организации питания, водоснабжения, очистки и обеззараживания сточных вод, об изменениях санитарно-гигиенических условий в детских дошкольных учреждениях. Чем крупнее изучаемый город, чем сложнее в нем перечисленные системы, тем труднее логически интегрировать степень влияния всех перечисленных переменных на развитие эпидемического процесса и заболеваемость населения. Важно вычленить в анализируемом периоде этапы, когда имела место действительная перестройка в каком-то из элементов социально-экономической организации населения, способная вызвать существенные изменения в проявлениях эпидемического процесса.

Как показывают результаты анализа причин и условий развития эпидемического процесса при кишечных инфекциях на разных территориях и в разных группах населения, в последние 10—15 лет рост качества и эффективности профилактических мероприятий замедлился. Система профилактики дизентерии и других кишечных инфекций остается относительно постоянной. Как было отмечено в первых главах книги, она позволяет в относительной мере контролировать развитие эпидемического процесса. Но темпы снижения заболеваемости постепенно замедляются. Поэтому чаще всего для описания тенденции эпидемического процесса наиболее адекватными оказываются функции с постоянным относительным приростом, т. е. линеаризуемые. Для таких функций величина абсолютного прироста убывает с увеличением значений независимой переменной, т. е. порядкового номера года.

Наиболее эффективно при подборе функций для описания многолетней тенденции заболеваемости сочетание логических и формально-статистических методов. Реализовать такое сочетание можно, если при программировании задачи предусмотреть диалоговый режим работы эпидемиолога с ЭВМ.

Многолетнюю тенденцию заболеваемости характеризуют по ее направленности и скорости изменений показателей динамического ряда. Направление тенденций (рост, снижение) определяют по знаку при коэффициенте регрессии b и уравнении, которое принято как адекватное для ее описания. Скорость изменений в динамическом ряду характеризуют показателем среднего темпа прироста, который считают статистически достоверным, если при его получении использована адекватная функция со статистически достоверными параметрами.

Рис. 3. Классификация периодов (а, б, в) по характеру и выраженности многолетней тенденции заболеваемости на примере дизентерии Зонне в 1953—1984 гг.

При анализе динамики заболеваемости за особо длительные периоды возможны затруднения с подбором просто интерпретируемых функций. Связано это с наличием длинноволновой периодичности в процессе. В таком случае анализируемый период можно разделить на несколько интервалов и провести их оценку раздельно. Так, на рис.3 период в 32 года, весьма неоднозначный по проявлениям эпидемического процесса, разделен на три интервала. В первом (а) — до 1965 г. отчетливая периодичность сочеталась с умеренной тенденцией к снижению по кривой показательной функции ( ). Далее до 1974 г. (б) основными были проявления периодичности, тенденция практически отсутствовала. После 1975 г. (в) она вновь выявилась как линейная, но уже более явная ( ). При таком «фрагментарном» подходе к анализу динамики заболеваемости становится ясным, что дальнейшее более детальное изучение проявлений эпидемического процесса целесообразно проводить раздельно для каждого из трех интервалов.

Если полученные параметры уравнения тенденции оказываются статистически недостоверными, то динамический ряд можно считать относительно стабильным. В таком случае, а также при истинной стабилизации заболеваемости, для характеристики ряда вычисляют показатели среднего уровня (среднюю арифметическую или медиану).

Оценка многолетней периодичности. Выявление периодической компоненты в эпидемическом процессе и ее количественную оценку мы проводим в основном с использованием метода автокорреляционного анализа. Лишь в особо сложных и ответственных задачах применяется переход от автокорреляционной функции к спектральной плотности процесса. Оба метода реализуются с использованием математического аппарата, наложенного Т. Anderson (1976).

Для вычисления коэффициента автокорреляции из исходных показателей вычитают теоретические значения, вычисленные по уравнению тенденции. Из полученного ряда отклонений от линии тенденции, последовательно сдвигаясь ни лет ( 1,2, 3, ... , n- ), создают второй ряд «зависимой» переменной. Коэффициент автокорреляции при запаздывании (лаге) на периодов вычисляют по формуле:

             (1)

При малом числе наблюдений его целесообразно корригировать по формуле, рекомендуемой В. Ю. Урбахом (1975):

        (2)

где n - число коррелируемых пар.

Вероятностную оценку и интерпретацию показателя производят, как и в случае обычного коэффициента корреляции.

Используя параметры тенденции и автокорреляции динамического ряда, можно построить ориентировочный прогноз заболеваемости на ближайшие годы методом экстраполяции или аналого-инерционным.

Пусть в интересующий нас момент времени t математическое ожидание уровня заболеваемости равно (t) и оно может быть получено по уравнению тенденции, а кроме того, в интервале времени Т возможна реализация k гармоник с определенным периодом , начальной фазой ; и амплитудой (j=1, 2, ... , k). Тогда прогностическое уравнение можно представить в обобщенном виде как:

             (3)

Здесь периодическая компонента эпидемического процесса представляется в виде простой суммы элементарных стационарных гармоник. Рассматривая реальную динамику заболеваемости, мы видели, что такой стационарности в эпидемическом процессе нет. Поэтому вторую половину уравнения (3) целесообразно заменить суммой периодических величин, каждая из которых задается выражением:

                (4)

где — коэффициент автокорреляции при лаге в лет.

Поскольку мы оперировали не исходными показателями заболеваемости, а их отклонениями от тренда, у которых математическое ожидание =0 , то выражение (4) для каждой из периодик процесса может быть заменено авторегрессией:

             (5)

Возможности применения зависимостей (3—5) при прогнозировании эпидемического процесса ограничиваются, так как необходимые для них предположения инерционности и стационарности динамических рядов не выполняются в достаточной мере. Периодики в эпидемическом процессе весьма изменчивы по всем своим параметрам. Чем длительнее период анализа, тем многообразнее динамика периодических компонент. Чем короче период, тем меньше шансов получить статистически надежную оценку параметров этих периодик и учесть их в прогностической модели.

Из рассмотрения динамики заболеваемости дизентерией Зонне в Ленинграде за 1953—1984 гг. мы сделали вывод о качественной неравнозначности отдельных периодов, особенно о своеобразии периода после 1975 г. Решение задач прогнозирования заболеваемости по столь краткой предыстории процесса (10 лет) на основе методов гармонического анализа не приведет к получению статистически надежных результатов. Более перспективен подход, выраженный уравнением (5), хотя и он с учетом множественности периодик и разной степени их нестационарности нуждается в дополнениях.

Разработка упрощенной прогностической модели с учетом многолетней тенденции и выраженной автокорреляции в ряду отклонений фактических показателей от нее проходит следующие этапы:

— построение исходного динамического ряда показателей заболеваемости выравнивание его по м.н.к. с учетом логических и статистических критериев выбора апроксимирующей функции;

— расчет по уравнению тенденции показателей теоретического ряда и их отклонений от фактических значений ;

— автокорреляционный анализ ряда или фильтрация процесса по методу скользящей средней для выделения основных периодик;

— построение для каждой из выделенных периодик регрессии   по и оценка параметров полученных уравнений;

— построение теоретического ряда показателей с учетом тенденции и выявленных периодик, начиная с +1 года, где - максимальная длина волны среди выделенных значимых периодик;

— вычисление отклонений , остаточной дисперсии и объясненной дисперсии , оценка адекватности полученной прогностической модели;

— вычисление средней квадратической ошибки прогноза;

— расчет ожидаемых по прогностической модели уровней заболеваемости на следующие годы, но не более продолжительности наиболее короткого из учтенных эпидемических циклов, при заданном уровне доверия.