| Главная | Реферат | Библиотека | Ссылки | Отчет о поиске | Индивидуальное задание |
Исходный URL: http://www.user.cityline.ru/~alphasys/downr.html
Нейронные сети с ядерной организацией являются структурным расширением класса многослойных сетей прямого распространения. Наполнение нового класса осуществляется за счет целенаправленного ограничения связей между нейронами. Концепция структурной организации ядерных сетей основана на понятии нейронного ядра, т.е. подмножества нейронов, которые имеют общее рецепторное поле. При этом постулируется, что рецепторные поля нейронных ядер не пересекаются. Нейронное ядро на структурном уровне определяется парой чисел: размерностью рецепторного поля и числом нейронов в ядре.
В многослойных сетях нейронные ядра связаны между собой проектирующими операторами перехода, для которых структурной характеристикой является ранг оператора. Поставив в соответствие каждому ядру вершину направленного графа, а каждому проектирующему оператору направленную дугу, получим новое графическое отображение нейронной сети, названное в работе [1] структурной моделью. На рис.1 показан пример двухслойной сети с ядерной организацией в классическом представлении, где каждая вершина соответствует одному нейрону, а дуги определяют связи между нейронами. На рис.2 приведена структурная модель, соответствующая приведенному примеру, где вершинам графа соответствуют уже нейронные ядра.

Обработка данных в каждом ядре i слоя m определяется нелинейным оператором
![]() так, что
так, что
 (1)
(1)
Передача между ядрами задается проектирующими операторами
![]() . Поскольку рецепторные поля нейронных ядер не пересекаются, то полный оператор нейронного слоя можно представить прямой суммой операторов ядер
. Поскольку рецепторные поля нейронных ядер не пересекаются, то полный оператор нейронного слоя можно представить прямой суммой операторов ядер
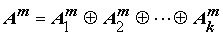
при этом межслойные передачи реализуются ортогональными проектирующими операторами, причем
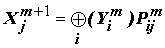 (2)
(2)
Последнее выражение по форме совпадает с правилом умножения вектора на матрицу с элементами
![]() , где координатами "вектора" являются компоненты
, где координатами "вектора" являются компоненты
![]() . Аналогично можно считать, что выражение (1) представляет собой умножение "вектора"
. Аналогично можно считать, что выражение (1) представляет собой умножение "вектора"
![]() на диагональную матрицу с элементами
на диагональную матрицу с элементами
![]() .Формально, следуя правилу умножения вектора на матрицы, из (1) и (2) нетрудно получить символическое выражение для преобразования данных в n-слойной нейронной сети :
.Формально, следуя правилу умножения вектора на матрицы, из (1) и (2) нетрудно получить символическое выражение для преобразования данных в n-слойной нейронной сети :
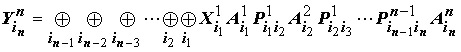 (3)
(3)
В нелинейных системах принцип суперпозиции не выполняется и операторные произведения не ассоциативны. В последнем выражении скобки, определяющие последовательность операций, не расставлены, но предполагается, что все операции над входным вектором выполняются строго в порядке следования нейронных слоев, начиная с первого.
Операторы нейронного слоя осуществляют отображение вектора из пространства рецепторов в пространство аксонов. Эту пару пространств в дальнейшем будем называть собственными пространствами нейронного слоя. Для перехода к матричной форме необходимо выбрать базисы в собственных пространствах. В большой степени этот выбор уже предопределен условиями ортогональности проектирующих операторов, которые вводят градуировку [2] в собственных пространствах. Целесообразно выбрать предельный случай градуировки, когда собственные пространства разбиваются в прямую сумму одномерных подпространств (базовых направлений). Такой вариант приемлем для любых структурных моделей ядерных сетей. При наличии градуировки базисные векторы всегда выбираются так, чтобы они принадлежали базовым направлениям. Принятый подход естественным образом приводит к понятию топологии нейронного ядра и топологии межъядерных связей [3]. Топология ядра определяется числовыми частичными отображениями:
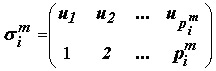

где
![]() - размер рецепторного поля ядра i слоя m,
- размер рецепторного поля ядра i слоя m,
![]() - число нейронов в ядре, u - номер базисного вектора в рецепторном пространстве слоя, v - номер базисного вектора в аксоновом пространстве. Следуя формализму линейных представлений групп [4], выделение векторных компонент
- число нейронов в ядре, u - номер базисного вектора в рецепторном пространстве слоя, v - номер базисного вектора в аксоновом пространстве. Следуя формализму линейных представлений групп [4], выделение векторных компонент
![]() будем рассматривать как действие частичных подстановок
будем рассматривать как действие частичных подстановок
![]() на векторы
на векторы
![]() и записывать эту операцию в виде:
и записывать эту операцию в виде:
![]()
![]() (4)
(4)
Поскольку рецепторные поля ядер не пересекаются, то:
![]() для любых i≠j. (5)
для любых i≠j. (5)
При выбранной градуировке смежные нейронные слои связаны между собой перестановочным оператором, действие которого определено подстановкой qm:
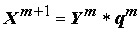 (6)
(6)
Операторы межслойного перехода индуцируют локальные операторы связи между нейронными ядрами так, что
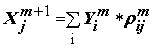 (7)
(7)
где
![]() - частичная подстановка, соответствующая операторам проектирования. Символ Σ обозначает в данном случае прямую сумму векторов. Из выражений (4), (6) и (7) при условии (5) следует
- частичная подстановка, соответствующая операторам проектирования. Символ Σ обозначает в данном случае прямую сумму векторов. Из выражений (4), (6) и (7) при условии (5) следует
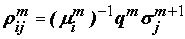
В матричном представлении действие оператора нейронного ядра можно записать в виде:

где
![]() - синаптическая карта ядра,
- синаптическая карта ядра,
![]() - многомерная функция активации. В координатной форме последние выражения можно представить следующим образом:
- многомерная функция активации. В координатной форме последние выражения можно представить следующим образом:
 (8)
(8)
 (9)
(9)
где a,b - индексы локальных координат. Передача данных между ядрами в координатной форме в соответствии с (7) определяется правилом:
 (10)
(10)
Выражения (8), (9), (10) полностью определяют алгоритм обработки данных в нейронной сети с ядерной организацией.
Данная работа поддержана грантом Минобразования РФ.
Список литературы
1. Дорогов А.Ю., Алексеев А.А. Математические модели быстрых нейронных сетей. В сб. научн. тр. СПбГЭТУ "Системы управления и обработки информации". Вып.490, 1996.
2. А.И. Кострикин, Ю.М. Манин. Линейная алгебра и геометрия. М.:- «Наука» - 1986.
3. Дорогов А.Ю. Структурные модели и топологическое проектирование быстрых нейронных сетей // Доклады международной конференции "Информационные средства и технологии" 21-23 октября 1997г. г.Москва, т1, с264-269.
4. Кострикин А.И. Введение в алгебру. Основы алгебры. - М.: Физматлит. 1994, -320с.
< /p>
| Главная | Реферат | Библиотека | Ссылки | Отчет о поиске | Индивидуальное задание |