1. RESEARCH FIELD OVERVIEW

Today, image processing has become one of the most interesting and highly developed branches of computer technologies. Texture analysis is a fundamental issue in image processing, computer vision and their applications, such as object recognition, remote sensing, content-based image retrieval and so on.

Nowadays, specialized computer diagnostic systems are widespread in Ukrainian medical centers. However, the majority of such systems do not use all the power of modern computer technologies.

My master’s work purpose is to make an automated system applied to image texture recognition using rotation and scale invariant methods.

This system can be adapted for using it in different industries, for example in medicine – for ultrasonic image processing, in metallurgy – for metal surface quality analyzing, and even in food industry – for meet quality examine.

The process of making this system is divided into two major steps:

1. image processing (texture analysis),
2. making decisions.

The most important thing is to work out a mathematical algorithm for the first step.

Image processing (image segmentation) can be viewed as the process of classifying regions in a picture into groups with common properties (texture). A difficulty arising is that common texture can be classified differently when viewed at different scales and rotated viewpoints.

2. METHODS REVIEW

2.1. Rotation Invariant Texture Classification Method Based on New Texture Signatures Extracted from Spectrum.

Fourier analysis has been considered as a powerful tool in invariant texture analysis. A new proposed method is computationally simple but efficient for rotation invariant texture recognition. Based on rotation spectrum representation of a texture image, a signature distribution function is obtained. By applying the Fourier expansion on this function, rotation invariance is achieved.

Jianguo Zhang and Tieniu Tan [1] examined the usefulness of these proposed features with a database of 1000 randomly rotated textures. Extensive comparative study with Gabor features shows that the proposed algorithm is highly efficient in invariant texture classification.

Here is an algorithm of computing the new texture signatures.

Let f(x,y) be the original texture image. Define the projection of f(x,y) onto a line l at angle with the x-axis as follows:

where

(2.1)

In the special case of =0, we obtain the vertical projection onto the x-axis:

(2.2)

The projection function can capture the regularity of textures at different orientations.

The following shows that the projection of f (x, y) onto a line at angle can be evaluated by its Fourier version at the line at .

Let f_r(x_r,y_r) be the rotated version of f(x,y). Then the relationship of these two images is formulated as follows:

fr(xr,yr)=f(x,y);

(2.3)

It is well known that when the original texture rotated by an angle, the frequency spectrum is also rotated by the same angle (this is the rotation property of the Fourier transform). The relationship between the spectra of the original and rotated image is described as follows:

(2.4)

where is the Fourier transform of the original texture f(x,y),

is that of f_r(x_r,y_r),

- is the inverse of the transpose of matrix R.

The one-dimensional Fourier transform of Equation (2.2) is:

(2.5)

P(u) can also be written in another form:

(2.6)

Let , be the Fourier transform of the projection of f (x, y) onto a line at angle and that of the Projection of f_r(x_r,y_r) onto a line at angle . Their relationship can be represented as follows:

=

(2.7)

central moment of Equation (2.7) are:

(2.8)

where are the mean value of .

Compute the spectrum signatures at angle and (=+) as follows:

(2.9)

Such that we have obtained the orientation spectrum signatures T(). It is obvious that the texture signature is rotation dependent and it is a periodic function of with a period of 2.

It is not difficult to see that T()=T() if -=. This implies that a rotation of the input image f (x, y) by is equivalent to a translation of its spectrum signatures by the same amount along the orientation axis.

Figure 2.1 shows the overall scheme of the extraction of the rotation invariant texture features.

Fig. 2.1. Schematic diagram of the rotation invariant texture feature extraction algorithm

2.2. Scale and Rotation Invariant Texture Features from the Dual-Tree Complex Wavelet Transform

The DT-CWT [2] is a form of DWT that generates complex valued coefficients. It is implemented with dual-trees of filters that independently generate the real and imaginary responses. Properties of the DT-CWT include:

• Approximate shift invariance.
• Filters in 2D exhibit directional selectivity.
• Perfect signal reconstruction from coefficients.
• Limited redundancy, 2:1 in 1D and 4:1 in 2D.
• Efficient computation O(n) for 1D, O(n²) for 2D.

In 2D, the filters are similar to Gabor filters, so the DT-CWT can be an efficient way of generating Gabor-like response coefficients. At each level, it generates 6 subbands that detect features spaced 30^o apart.

The DWT provides a multi-scale analysis tool for looking at signals. It can be viewed as a band-pass filter whose filters are sensitive to frequencies over dyadic scales. At each level of analysis, the input signal is decomposed into functions of wavelet basis functions

(2.10)

such that Ф defines the mother wavelet, the integer s describes the scale of analysis while k defines the shift. The wavelet basis functions for the DT-CWT are scaled in the same way as the DWT.

For scale invariant feature analysis, we desire filters that are equal in amplitude at each level of analysis and so we remove the scaling factor of 2^-s/2. The new family of wavelet basis functions is generated by

Fortunately, we do not have to modify the filters in the DT-CWT but instead, we only need to multiply the DT-CWT output coefficients by 2^-s/2. For ease of reference, we denote DT-CWT^# and DWT^# as the transforms that use Ф^#_s,k(x) for their wavelet basis functions.

2.3. Log-Polar Wavelet Energy Signatures for Rotation and Scale Invariant Texture Classification

This method [3] proposes an effective scheme for rotation and scale invariant texture classification using log-polar wavelet signatures. The rotation and scale invariant feature extraction for a given image involves applying a log-polar transform to eliminate the rotation and scale effects, but at same time produce a row shifted log-polar image, which is then passed to an adaptive row shift invariant wavelet packet transform to eliminate the row shift effects. So, the output wavelet coefficients are rotation and scale invariant.

The adaptive row shift invariant wavelet packet transform is quite efficient with only O(n*log(n)) complexity. A feature vector of the most dominant log-polar wavelet energy signatures extracted from each subband of wavelet coefficients is constructed for rotation and scale invariant texture classification. In the experiments, a Mahalanobis classifier is employed to classify a set of 25 distinct natural textures selected from the Brodatz album.

The experimental results, based on different testing data sets for images with different orientations and scales, show that the proposed classification scheme using log-polar wavelet signatures outperforms two other texture classification methods, its overall accuracy rate for joint rotation and scale invariance being 90.8 percent, demonstrating that the extracted energy signatures are effective rotation and scale invariant features. Concerning its robustness to noise, the classification scheme also performs better than the other methods.

Fig. 2.2. Decomposition of rotation and scale invariant wavelet coefficients from a rotated and scaled texture image.

Log-polar transform algorithm consists of two major steps. In the first step, the radius of the largest circle inside the given square image is used as a scan line to sample S times from 0^o до 360^o to produce its equivalent Sx[N/2] polar form. So, formally, a polar form p(a,r) of the given NxN image f(x,y) can be computed as follows:

(2.12)

for а=0,…,S-1, and r=0,…,[N/2]-1.

In the second step, logarithm functions are applied to all radii values in the polar form and their ouputs are then quantized into R bins. Hence, an SxR log-polar image for the given NxN image is produced. The procedure can be formally defined as follows:

(2.13)

for i=0,…,S-1, and j=0,…,R-1.

3. SCIENTIFIC RESEARCH RESULTS

Summarizing viewed methods: rotation invariant texture classification method based on new texture signatures extracted from spectrum, scale and rotation invariant texture features from the dual-tree complex wavelet transform method, log-polar wavelet energy signatures for rotation and scale invariant texture classification method; several major conclusions are achieved:

• texture classification method based on new texture signatures extracted from spectrum obtain rather high average classification accuracy of 98.90%. However, this method is only rotation but not scale invariant. Because of this lack this method is not feasible to my muster’s work in the way it is. Nevertheless, it is possible to improve the method. For example, we can make an attempt to use one of existing transforms (Radon or log-polar) before or after feature vector extraction to achieve scale invariance.
• rotation and scale invariance in texture analysis methods can be obtained in two ways:
  1. with the help of image transform before or after feature vector extraction. We could use Radon or log-polar transform in order to achieve rotation and scale invariance.
  2. by using rotation and scale invariant texture features.

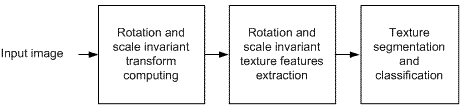
As we have analyzed represented methods, we can make a schematic diagram of rotation and scale invariant image processing (Figure 3.1).

Fig. 3.1. Schematic diagram of rotation and scale invariant image processing

Classification is the process of image elements distribution by classes based on their attributes (features) meaning [4].

REFERENCES

[1] J. Zhang and Tieniu Tan, “New Texture Signatures and Their Use in Rotation Invariant Texture Classification”, IEEE Trans. Image Processing, vol. 8, Feb. 2001.

[2] M. Pickering, M. Frater and J. Arnold, “Scale and Rotation Invariant Texture Features From the Dual-Tree Complex Wavelet Transform”, IEEE Trans. Image Processing, vol. 2, June 2004.

[3] C.-M. Pun and M.-C. Lee, “Log-Polar Wavelet Energy Signatures for Rotation and Scale Invariant Texture Classification”, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 25, no. 5, May 2003.

[4] http://gis-lab.info/qa/genclass-erdas.html – информация о классификации изображений.

Note:

This autoreferat is not the final version of master's work autoreferat. Master's work is supposed to be ready in December '06. To get the final version e-mail the author.