При резании металлов на участках фактического контакта инструмента с обрабатываемым материалом образуются мостики схватывания. При схватывании двух металлических материалов между ними образуется металлическая связь. Благодаря осуществлению химической связи, между контактирующими телами происходит перераспределение электронов, их частные зоны и локальные уровни преобразуются в общие зоны и уровни, и устанавливается единый уровень Ферми [1], полная энергия системы понижается.

Главной характеристикой схватывания металлов является прочность адгезионных связей на срез, зависящая от химического состава поверхностей (наличия примесей и дефектов) и условий контактирования металлов (температур, нормальных нагрузок). Прочность адгезионных связей влияет на величину силы трения в контакте, вызывающей образование тепла и создающей напряженное состояние в приповерхностных слоях материалов, определяет соотношение длин зон внутреннего и внешнего трения, влияет на стабильность наростообразования и др. Экспериментально также показано, что интенсивность изнашивания инструмента может определяться отношением прочности адгезионных связей на срез к микротвердости инструментального материала при данных условиях обработки [3]. Для ее определения придется воспользоваться методами, разработанными в квантовой теории твердого тела.

Исследование лучше всего начать с простейшего случая контакта двух бездефектных, беспримесных металлических монокристаллов, моделирующих контакт единичных микронеровностей.

Порядок расчета предлагается следующий:

1. расчет полной энергии системы электронов каждого кристалла;
2. расчет спектра энергетических уровней и полной энергии системы электронов комбинированного кристалла, полученного путем совмещения двух исследуемых монокристаллов;
3. расчет энергии, выделившейся при совмещении кристаллов.

Совмещение кристаллов сопровождается общей перестройкой энергетических уровней, исчезновением поверхностных электронных состояний и высвобождением соответствующего количества энергии. Уровень этой энергии и будет характеризовать усилие, необходимое для разрыва адгезионной связи, а также долю тепла, образующегося при трении.

Расчет одноэлектронных состояний в твердом теле может проводиться в кластерном приближении [4], [5]. Он заключается в моделировании кристалла изолированной группировкой атомов и расчете электронной структуры такого фрагмента при помощи математического аппарата, разработанного в квантовой химии молекул. Кластерный подход обладает рядом следующих достоинств: небольшие затраты машинного времени, возможность расчета не только симметричных фрагментов, но и всевозможных отклонений от стехиометрии – примесных атомов, локальных дефектов, искажений кристаллической решетки соединения. Кластерные методы могут использоваться и для исследований поверхностных явлений. Основным недостатком кластерного метода является необходимость учета граничных эффектов (поля кристалла).

Исследования применимости кластерного метода к расчетам электронной структуры различных материалов показали, что кластерные модели особенно хорошо применимы к кругу металлов, сплавов и соединений d- и f-элементов, содержащих в значительной степени локализованные d- и сильно локализованные f-электроны. К таким материалам относятся, например, железо, никель, молибден, хром, титан, вольфрам, тантал, карбиды титана, вольфрама, тантала, циркония и другие.

В наиболее широко известном методе Хa -РВ используется muffin-tin-форма аппроксимации локального потенциала , хорошо известная в зонных методах. В кластере выделяют три области (см. рис.). Область I составляют центрированные на атомах сферы, внутри которых потенциал принимается сферически-усредненным. Область II — пространство между атомными сферами и окружающей кластер внешней сферой, где потенциал полагается усредненным по объему (постоянным). Наконец, в III — вне внешней сферы — потенциал вновь сферически-симметричен. Обычно полагают, что атомные сферы касаются друг друга, а их радиусы вычисляют по процедуре Нормана.Такое представление потенциала позволяет ввести быстро сходящееся разложение по парциальным волнам, в качестве решения уравнения Хартри – Фока – Слэтера.

Внутри каждой атомной сферы I радиуса b_i волновую функцию ψ_i можно представить в виде разложения по сферическим гармоникам Y_lm(r):

Аналогичное представление используют и для внекластерной области III. В межсферном пространстве молекулярная орбиталь разлагается в ряд по сферическим функциям Бесселя и Неймана – j_l и n_l .

Из условия непрерывности Y _i и ее производной на границах MT-сфер получается система уравнений, позволяющая определить электронный энергетический спектр рассчитываемого кристалла или молекулы.

Простейший вариант расчета энергии адгезии можно произвести на примере взаимодействия меди с железом:

Тип симметрии : C_4v; - линейная комбинация симметризованных орбиталей (СО) кластеров Cu и Fe.

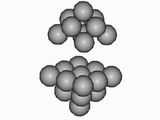
Рис. 2 Кластеры Fe и Cu со свободной поверхностью, до схватывания

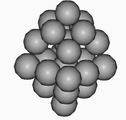
Рис. 3 Кластеры Fe и Cu, в состоянии схватывания.

После рассмотрения чистых металлов следует усложнить расчет, исследуя контакт твердого раствора с фазой внедрения ( сталь с WC ,TiC и др. ), что имеет место при резании.

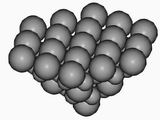
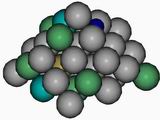
Рис. 4 Кластеры карбида вольфрама (WC), карбида титана (TiC) и жаростойкой стали 12Х18Н9

Тип кристаллической решетки WC – гексагональная; параметры решетки a=2,91 å , c=2,84 å ; тип симметрии кластера С_6v.

Тип кристаллической решетки TiC – кубическая; параметр решетки a_TiC=4,32 å ; тип симметрии кластера С_4v.

Тип кристаллической решетки жаростойкой стали 12Х18Н9 – ОЦК; параметр решетки a_12Х18Н9=2,86 å .

Рис. 5 Кластеры WC и TiC в состоянии схватывания со сталью 12Х18Н9

Далее в расчетах необходимо учесть наличие дефектов и примесей на поверхностях контакта и построить зависимость энергии адгезии от температуры и нормальных давлений с целью теоретического выявления распределения касательных напряжений и интенсивности тепловыделений на длине контакта по задней и передней поверхностей инструмента.

В настоящее время ведется разработка программного обеспечения для осуществления описанных выше расчетов.

ЛИТЕРАТУРА

1. Алесковский В. Б. Химия твердых веществ. – М.: Высшая школа, 1978. – 256 с., ил.
2. Кащеев В. Н. Процессы в зоне фрикционного контакта металлов. – М.: Машиностроение, 1978. – 213 с., ил.
3. Шустер Л. Ш. Адгезионное взаимодействие режущего инструмента с обрабатываемым материалом. – М.: Машиностроение, 1988, 96 с.: ил.
4. Слэтер Дж. Методы самосогласованного поля для молекул и твердых тел. М.: Мир, 1978. – 663 с.
5. Губанов В.А., Курмаев Э.З., Ивановский А. Л. Квантовая химия твердого тела. – М.: Наука, 1984. – 304 с.

http://www.ostu.ru/conf/tech2002/sect5/michryutin/michryutin.html