МОДЕЛИРОВАНИЕ ТЕМПЕРАТУРНОГО РЕЖИМА
РАБОТЫ ПОДШИПНИКОВОГО УЗЛА
ЗАКАЛЕННАЯ
СТАЛЬ – КЕРАМИКА
Молчанов А.Д., Рожков Д.Б. (ДонГТУ, г. Донецк, Украина)
In the given work the problem of determination of temperature in a zone of friction of the ceramic bearing of a sliding is considered and the modelling of temperature operational mode for want of various pressure and porosity of ceramics is made.
В современном машиностроении все более широкое применение, вследствие уникальных физико-механических свойств находят подшипниковые узлы с применением конструкционной керамики. Основное их отличие от подшипников с металлическими вкладышами - более низкая теплопроводность керамики, вследствие чего затруднен теплоотвод и возникает необходимость экспериментального исследования и математического моделирования температурного режима в зоне трения с целью выбора оптимального конструктивного решения, изучения влияния свойств материала и условий эксплуатации.
Рассматривается задача определения температуры в зоне трения пористого керамического подшипника скольжения (рис.1).
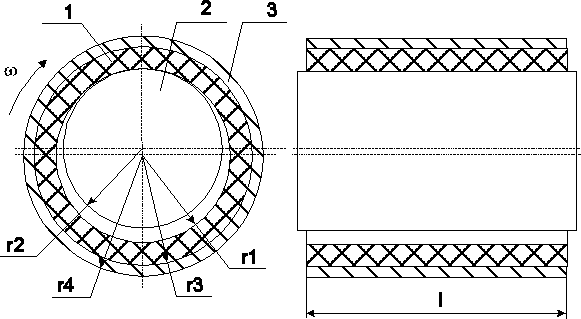
Рис. 1. Подшипниковый узел
1-керамическая подшипниковая
втулка; 2-стальной вал; 3-стальная обойма для закрепления подшипниковой
втулки
Допущения, принятые при расчете:
- Подшипниковый узел работает по обратной схеме : вращающийся подшипник скольжения –неподвижный вал;
- Работа подшипникового узла происходит при граничном режиме смазывания – за счет выделения смазочного материала из пор подшипниковой втулки;
- Износ керамической втулки значительно меньше износа стального вала. По мере увеличения износа увеличивается фактическая площадь контакта.
Искомым параметром является температура в зоне контакта
сопряжения стальной вал - керамическая втулка.
Уравнение теплового баланса
при работе подшипникового узла в дифференциальной форме [1]:
dQтp= dQa+ dQп+dQв,
где dQтp - количество тепла, выделившегося при трении
за бесконечно малый промежуток времени dτ;
dQа - количество тепла, аккумулированного
подшипниковым узлом;
dQп - количество тепла, прошедшего через корпус
подшипника и отведенного в окружающий воздух за время dτ;
dQв - количество тепла, отведенного валом в окружающее
пространство за время dτ.
Известно [2], что
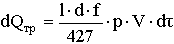 ,
,где l и d - длина и диаметр подшипника;
f - коэффициент
трения;
p - контактное давление;
V - скорость скольжения.
Тепло, аккумулированное подшипниковым узлом:
dQa=∑Gi·Ci·dτ,
где ∑Gi-вес элементов подшипникового
узла;
Ci -удельная теплоемкость элементов подшипникового
узла.
По закону Фурье и формуле Ньютона-Рихмана получаем выражение для
dQп [3]:
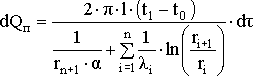 ,
,где t1 -температура на поверхности
контакта;
to - температура окружающей среды;
α - коэффициент
теплоотдачи;
λ - коэффициент теплопроводности.
Количество тепла, отводимого валом в окружающее пространство:
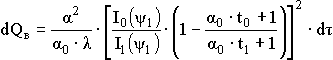 ,
,где I0(ψ1) -функция Бесселя первого рода
нулевого порядка;
I1(ψ1) -функция Бесселя первого рода
первого порядка.
Решая уравнение теплового баланса можно найти температуру в зоне контакта. Экспериментальное определение температуры в зоне контакта производили при помощи медь-константановых термопар, вмонтированных в вал. Обработка данных производилась с помощью метода наименьших квадратов в среде MathCAD 7.0 pro. Анализ результатов показал:
- Теоретические кривые роста температуры находятся в пределах дисперсии экспериментальных значений.
- В начальный момент времени работы подшипникового узла наблюдается рост температуры. Через 20…60 минут работы, в зависимости от давления и пористости, наблюдается стабилизация температурного режима. Увеличение давления приводит к росту температуры стабилизации. При меньшей пористости наблюдается меньшая температура стабилизации, что согласуется с лучшей теплопроводностью более плотной керамики.
- Применение принудительного охлаждения позволяет кардинально изменить температурное состояние узла трения. В первые минуты работы рост температуры одинаков при работе без охлаждения. В дальнейшем рост температуры протекает с различной скоростью и уже на пятой минуте работы наступает стабилизация температурного режима работы подшипникового узла, в то время как при естественном охлаждении стабилизация наступает за период в 10 раз более длительный. При охлаждении обдувом с интенсивностью 5 м3/мин температура стабилизации в 2 раза меньше, чем при естественном охлаждении. Высокая температура стабилизации и медленная стабилизация температурного режима работы подшипникового узла связаны с низкой теплопроводностью пористой керамики и затрудненным по этой причине отводом тепла в корпус подшипника.
Экспериментальные исследования показали, что изменение коэффициента трения от давления и температуры в зоне контакта носит нелинейный характер. В среде Mathcad 7.0 pro были получены зависимости коэффициента трения от температуры для двух значений пористости керамики (6,2% и 9,2%):
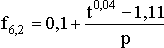 ,
,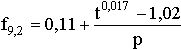 .
.Сравнение значений коэффициентов трения экспериментальных и
полученных по приведенным зависимостям показывает адекватность математических
моделей (критерий Фишера при уровне значимости 0,05).
Таким образом, для
обеспечения нормального теплового режима работы подшипникового узла закаленная
сталь-керамика необходимо обеспечить увеличение теплоотвода из зоны трения.
Список литературы: 1. Справочник по триботехнике /Под общ. ред. М. Хебды, А.В. Чичинадзе. В 3 т. – Т. 1. – М.: Маш., 1989. – 400 с. 2. Воронков Б. Д. Подшипники сухого трения. – Ленинград: Машиностроение. Ленингр. отд-ние, 1979. – 224 с. 3. Шнейдер П. Инженерные проблемы теплопроводности. – М.: Издательство иностранной литературы, 1960. – 478 с.
Молчанов А.Д., Рожков Д.Б. Моделирование темпратурного режима работы подшипникового узла закаленная сталь - керамика// Современные металлорежущие системы машиностроения. Материалы Всеукраинской студенческой конференции. - Донецк 10-13 апреля 2000 г. Донецк: ДонГТУ, 2000. - с. 71-75