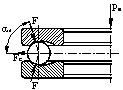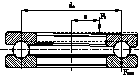Стручков Александр Александрович
ПОВЫШЕНИЕ НЕСУЩЕЙ СПОСОБНОСТИ, РЕСУРСА
И ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК УПОРНЫХ УЗЛОВ
РОТОРОВ ЗА СЧЕТ СОВМЕЩЕНИЯ ПОДШИПНИКОВ КАЧЕНИЯ И СКОЛЬЖЕНИЯ
( www.ostu.ru/science/defence/avtoreferat/struchkov.doc)
Расчет сил в элементах совмещенных опор
В первом разделе данной главы рассмотрены общие вопросы моделирования опор. Приведено обоснование выбора в качестве объекта исследования совмещенных опор, элементы которых расположены по параллельной схеме. Также в данном разделе представлена конструкция УСО (рис.1), являющаяся базовой для дальнейших исследований, описан принцип ее действия и особенности функционирования.
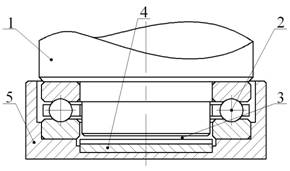
1-вал; 2 – упорный подшипник качения; 3 – гарантированный зазор; 4 – подпятник упорного гидродинамического подшипника cкольжения; 5 – корпус опоры.
Рис. 1 – Конструктивная схема упорной совмещенной опоры
Расчет и анализ рабочих характеристик УСО базируется на знании сил, действующих в элементах опоры. Последующие разделы второй главы посвящены расчетам упорных подшипников качения и скольжения.
Математическая модель определения сил в упорном шариковом подшипнике качения (УПК) основывается на решении контактной задачи Герца и строится на классических допущениях.
Согласно контактной задаче относительное
сближение 
колец упорного
подшипника качения в направлении осевой нагрузки 
равно:
,
(1)
где 
–
коэффициент пропорциональности, зависящий от кривизны соприкасающихся тел в
местах контакта и от упругих свойств материалов, из которых эти тела
изготовлены (коэффициент нелинейной жесткости подшипника качения размерностью
Н/мn);
,
(2)
здесь 2
-величина являющаяся отображением
геометрии контакта и определяемая в зависимости от вспомогательной величины 
;
- сумма главных
кривизн поверхностей соприкосновения тел в месте их первоначального контакта;
−
коэффициент, характеризующий упругие свойства материала, здесь 
(
) - соответственно,
коэффициенты Пуассона и модули упругости материалов контактирующих тел.
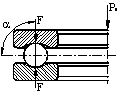
Математическая модель подшипника качения, рассматриваемая в данной работе учитывает влияние центробежных сил на угол контакта и случай не симметричной нагрузки (рис.2).
|
|
|
|
Рис. 2 – Схемы нагружения подшипника
С учетом допущений и расчетных схем подшипника восстанавливающая сила подшипника находится на основании решения следующей системы уравнений:
(3)
Определение сил трения в подшипнике качения основывается на полуэмпирической методике, разработанной и применяемой на ведущих предприятиях подшипниковой промышленности:
. (4)
Нахождение силовых факторов упорного гидродинамического подшипника скольжения с наклонными несущими поверхностями (УПС) (рис.3) основывается на интегрировании поля давлений, полученного в результате решения методом конечных разностей модифицированного уравнения Рейнольдса на случай двухмерного турбулентного течения вязкого сжимаемого смазочного материала:
(5)
.
(6)
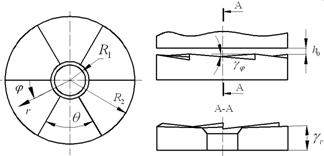
R1 – внутренний радиус подпятника; R2 – наружный радиус подпятника; 
– угол сегмента; 
– угол наклона поверхности в
радиальном направлении; 
– угол наклона поверхности в окружном
направлении; 
–
начальный осевой зазор.
Рис. 3 – Расчетная схема УГДП
Моделирование осевого зазора проводилось на основе уравнений наклонной плоскости, проходящей через три точки, и аппроксимации.
(7)
В качестве смазочных материалов в ходе исследования использовались вода и масло с начальной динамической вязкостью порядка 0.1 Па·с. В целях учета изменения теплофизических свойств смазочного материала были приняты известные аппроксимирующие функции, апробированные в работах других авторов.