Автоматизація технологічних об’єктів та процесів. Пошук молодих. Збірник наукових праць VI Міжнародної науково-технічної конференції аспірантів та студентів в м. Донецьку 24-27 квітня 2006р. – Донецьк: ДонНТУ, 2006. – С.145-147.
В период эксплуатации насосной установки по ряду причин происходит отклонение режима работы насосов от нормального, снижение эффективности и надежности работы установки. К рабочему режиму насоса предъявляется требование экономичности, оцениваемое допустимым значением коэффициента полезного действия, который определяет границы рабочей зоны насоса. Поэтому для экономичной работы насосной установки необходимо обеспечить нахождение режима в пределах рабочего участка характеристики. Однако это является необходимым, но недостаточным условием для эффективной работы насоса. Следует также учитывать возможность возникновения кавитации в потоке жидкости, движущемся по всасывающему трубопроводу, подводу и на входе в рабочее колесо насоса.
Поэтому разработка математической модели управления насосной установкой в зоне промышленного использования насоса, которая отсутствует в базовой аппаратуре автоматизации ВАВ.1М, используемой для управления водоотливной установкой, является актуальной задачей.
Для определения координат рабочего режима необходимо располагать напорными характеристиками насоса и трубопроводной сети. В результате исследований учеными института имени Федорова М.М. было получено следующее аналитическое выражение рабочей напорной характеристики насоса [1]:
Hм = z·(Hф.к– Bк·Q2),
где z – число колес насоса, 10; Hф.к – коэффициент начального давления при нулевой подаче, 73; Bк – поправочный коэффициент, 1.59·10-4; Q – текущее значение подачи, м3/ч.
Напорная характеристика трубопроводной сети в общем виде рассчитывается по следующей формуле:
Hс = Hг+а·Q2,
где Hс – соответственно общие потери напора в трубопроводной сети в целом, м; Hг – геометрическая высота водоподъема воды, м; а – коэффициент сопротивлений сети, с2/м5.
В качестве способа регулирования режима работы водоотливной установки используем дросселирование с помощью регулировочной задвижки – проходного вентиля тарельчатого типа.
Регулирование подачи насоса можно осуществить, изменяя местное гидравлическое сопротивление ξ:
ξ = 41,1·e-10,824·x,
которое зависит от степени открытия затвора, равного отношению линейного перемещения запорного органа δ, к проходному диаметру d вентиля:
x = δ/d,
принимаемое значение в диапазоне 0,05...0,45.
Для учета возможности возникновения кавитации, необходимо располагать характеристикой подводящего трубопровода:
Hвак = Hвс.г+авс·Q2,
и кавитационной характеристикой насоса:
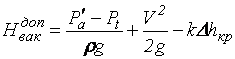
где Hвак – вакуумметрическая высота всасывания, м; Hвс.г – геометрическая высота всасывания насоса, м; 
– допустимая вакуумметрическая высота всасывания, м; 
– атмосферное давление на глубине шахты Н, Па; Pt – давление насыщенного пара воды, Па; V – средняя скорость воды в подводящем трубопроводе, м/с; ρ – плотность шахтной воды, кг/м3; Δhкр, – критический кавитационный запас, м; k – коэффициент запаса, 1,25.
На рисунке 1 приведен график изменения напорных характеристик трубопроводной сети на границах рабочей зоны насоса (при разных геометрических высотах водоподъема) в условиях безкавитационной работы установки.
Рисунок 1 – Графики: а) напорных характеристик трубопроводной сети при разных геометрических высотах водоподъема; б)
, Hвак в условиях безкавитационной работы установки
Построенные графики на рисунке 1 дают представление о значении подачи насоса Qн при регулировании с помощью степени открытия затвора проходного вентиля x , а также соответствующее ему значение уровня воды в водо-сборнике h. Эти данные можно использовать в уравнении изменения уровня воды в водосборнике:
F·dh(t)/dt = Qп–Qн(t),
где F – площадь приемной емкости, м2; dh(t)/dt – изменение уровня воды во времени; Qп – приток воды, м3/ч; Qн(t) – изменение подачи насоса во времени (точки пересечения напорных характеристик насоса и трубопроводной сети при регулировании с помощью вентиля).
Решение данного уравнения имеет следующий вид:
h = ∫(1/F·(Qп-Qн(t)))dt+C,
C = h0=1,1 м (при t=0).
На рисунке 2 приведен график изменения уровня воды в водосборнике во времени.
Рисунок 2 – Графики изменения уровня воды в водосборнике: а) на левой границе рабочей зоны; б) на правой границе рабочей зоны
Итак, как видно из рисунка 2, работа насосной установки наиболее эффективна во втором случае (на правой границе рабочей зоны насоса), поскольку время (Tпр.гр = 0,603 ч), за которое насос откачает воду с 1,1 до 2,151 м, меньше, чем время (Tлев.гр = 17,741 ч), за которое насос откачает воду с 1,1 до 4,648 м.
Полученная математическая модель может быть в дальнейшем использована в блоке управления насосной установкой в зоне промышленного использования насоса для определения уставок управления подачей насоса.
Перечень ссылок
1. Гейер В.Г., Тимошенко Г.М. Шахтные вентиляторные и водоотливные установки: Учебник для вузов. – М.: Недра, 1987. – 280с.