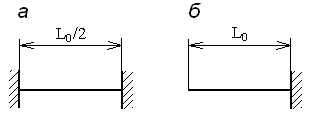
Рис. 1 - Схемы к расчету колебаний тягового органа при закритическом (а) и докритическом (б) натяжении
| Главная страница Библиотека Ссылки Отчет о поиске Индивидуальное задание |

 |
|
| агр = | |
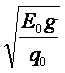 |
|
| апор = | |
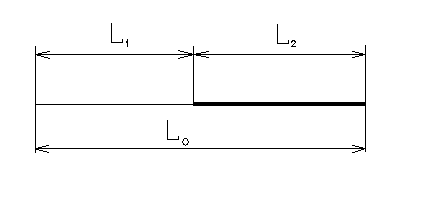
 |
|
| агр = | |
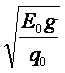 |
|
| апор = | |
 |
|
| Vзакр = | |


| Главная страница Библиотека Ссылки Отчет о поиске Индивидуальное задание |