|
В этой главе будут рассматриваться распределения элементов матриц, используемые для вычисления матричного произведения
с помощью параллельного алгоритма. Важно отметить два случая распределения (отображения):
блочно–линейное (block–linear) и рассеянное (scattered). Также будут приведены формулы
для описания этих видов отображений в зависимости от различных параметров. После будет определено понятие
перестановочной совместимости, которое необходимо для определения требований алгоритмической совместимости
матриц для параллельных алгоритмов вычисления матричного произведения. Будет рассматриваться перестановочно–совместимое
отображение данных (т.е. виртуальное 2–мерное распределение данных для решётки–тора) для отображения элементов матриц
на 2–мерную решётку вычислительных процессов. Будет представлено виртуальное 2–мерное распределение
данных, которое может быть использовано для решения потенциальной проблемы дисбаланса вычислительной нагрузки. В конце
будет строго определено свойство алгоритмической совместимости, соблюдение котрого гарантирует корректность вычисления
матричного произведения.
Распределение данных было формально определено van de Velde (1994), детальное определение распределения
данных может быть найдено у Skjellum (1990) или Skjellum и Baldwin (1991).
Определение 1 (Функции распределения данных): Функция распределения данных
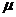 - отображение
1-к-1, - отображение
1-к-1, 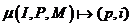 . Где: . Где:
- I – глобальное имя коэффициента
- P – число процессов, среди которых распределяются коэффициенты
- M – общее число коэффициентов
Пара (p, i) определяет процесс p (0 < p < P) и локальное для него имя коэффициента i из общего набора I.
Обратная функция распределения данных
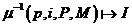 преобразует локальное имя i коэффициента для процесса p.
преобразует локальное имя i коэффициента для процесса p.
Функция кардинальности 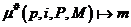 определяет число коэффициентов (m), которые распределяются по P процессам с помощью функции
отображения
определяет число коэффициентов (m), которые распределяются по P процессам с помощью функции
отображения 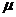 . .
Функция отображения описывает преобразование между глобальным пространством коэффициентов и локальным
процессом с индексным пространством. Поэтому, определённое распределение данных может быть описано с
помощью набора функций распределения данных. Функции распределения данных – базовые абстракции,
необходимые для реализации независимости от распределения данных (Data-Distribution-Independence, DDI).
Блочно–линейное распределение данных и блочно–рассеянное распределение данных – два вида
распределения данных. Набор глобальных коэффициентов определяется в два шага. На 1–ом, производится
разделение глобального множества коэффициентов на R блоков. Блоки могут отличаться размерами в зависимости
от того, является ли R делителем M. Однако, по возможности разбиение на группы M коэффициентов производится
с расчётом одинаковой длины групп. Если размеры блоков будут зафиксированы как
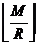 и
и  ,
размеры блоков могут отличаться максимум на 1 элемент. Размер блока с индексом t определяется по формуле (3.1). ,
размеры блоков могут отличаться максимум на 1 элемент. Размер блока с индексом t определяется по формуле (3.1).
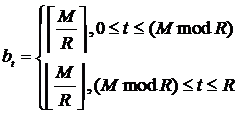 (3.1) (3.1)
На 2–ом шаге, производится последовательное распределение блоков по процессам. Последовательно
расположенные блоки закрепляются за различными процессами с фиксированным страйдом (stride) s.
Блок с индексом t закрепляется за процессом p, где связь величин t и p определяется формулой (3.2).
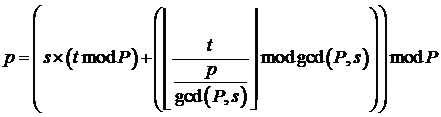 (3.2) (3.2)
Где s (1 <= s <= P) – страйд, а gcd – функция отыскания наибольшего общего делителя.
При выборе различных значений числа блоков R и страйда s могут быть получены многие распределения данных,
часть которых представляют особый интерес. При выборе R = P и s = 1 получается блочно–линейное
распределение данных. А при выборе R = M и s = 1 блочно–рассеянное распределение данных.
|