|
Ниже будет рассмотрено отображение матрицы на 2–мерную решётку процессов. Пусть узлы решётки процессов
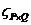 размерностью P×Q, обозначаются как (p, q), 1 < p < P–1, 1 < q < Q–1. Когда матрица A размерностью
M×N отображается на решётку процессов
размерностью P×Q, обозначаются как (p, q), 1 < p < P–1, 1 < q < Q–1. Когда матрица A размерностью
M×N отображается на решётку процессов
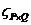 ,
производится отображение элементов матрицы в обоих измерениях. Для строк матрицы вводится функция
отображения ,
производится отображение элементов матрицы в обоих измерениях. Для строк матрицы вводится функция
отображения
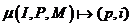 .
Для столбцов матрицы A вводится функция отображения .
Для столбцов матрицы A вводится функция отображения
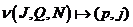 . .
Перестановочная совместимость определяется как свойство функций распределения данных.
Определение 2 (Перестановочная совместимость):
Два распределения данных
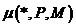 и
и
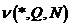 – перестановочно совместимы тогда и только тогда, когда M = N.
– перестановочно совместимы тогда и только тогда, когда M = N.
Для параллельного матричного произведения вида
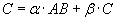 матрица A имеет размерность MA×NA, распределение строк
матрица A имеет размерность MA×NA, распределение строк
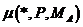 и распределение столбцов
и распределение столбцов
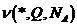 .
Матрица B имеет размерность MB×NB, распределение строк .
Матрица B имеет размерность MB×NB, распределение строк
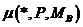 и
и
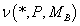 распределение столбцов . Вводя данные обозначения, можно перейти к обсуждению перестановочной
совместимости
распределение столбцов . Вводя данные обозначения, можно перейти к обсуждению перестановочной
совместимости
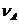 и
и
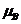 на исходной решётке процессов:
на исходной решётке процессов:
- обе функции отображения
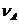 и
и
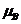 , определяющие блочно–линейное распределение, являются перестановочно совместимыми на
исходной решётке процессов;
, определяющие блочно–линейное распределение, являются перестановочно совместимыми на
исходной решётке процессов;
- обе функции отображения
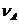 и
и
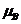 ,
определяющие блочно–рассеянное распределение, являются перестановочно–совместимыми в
случае квадратное решётки процессов (в случае неквадратной решётки процессов свойство
перестановочной совместимости не соблюдается, что обосновано разными значениями P и Q). ,
определяющие блочно–рассеянное распределение, являются перестановочно–совместимыми в
случае квадратное решётки процессов (в случае неквадратной решётки процессов свойство
перестановочной совместимости не соблюдается, что обосновано разными значениями P и Q).
Несоблюдение свойства перестановочной совместимости на прямоугольной (неквадратной сетке процессов)
для матриц–сомножителей создаёт проблему для параллельного вычисления произведения вида
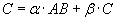 . В этом случае выполнение параллельного алгоритма влечёт за собой дополнительные накладные расходы
на коммуникацию при вычислении матричного произведение указанного выше вида.
. В этом случае выполнение параллельного алгоритма влечёт за собой дополнительные накладные расходы
на коммуникацию при вычислении матричного произведение указанного выше вида.
|