|
Неквадратную прямоугольную решётку можно рассматривать как виртуальную квадратную, размерностью
×
.
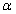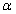В этом случае
–
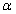наименьший общий сомножитель величин P и Q. В таком случае существует возможность
распределения элементов матриц–сомножителей на такую виртуальную решётку. Для описания отображения
может быть использована формула (3.3), модифицированная версия формулы (3.2).
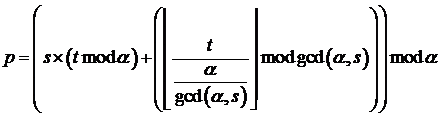(3.3)
Доказано, что при выборе одинаковых значений размера блока и страйда, отображения
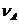и
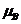перестановочно совместимы. При разделении процессов в квадратной виртуальной решётке может
иметь место проблема неравномерной загрузки вычислительных узлов в виду неравномерной работы,
выполняемой отдельными процессами. Это связано с тем, что процессы виртуальной решётки могут
объединять в себе неравное число физических процессов исходной прямоугольной решётки.
Для решения проблемы необходимо изменить стратегию распределения элементов матриц по процессам
решётки. Распределяемые элементы сначала разделяются на P частей так, чтобы последовательные
группы элементов имели размеры
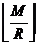и
 .
Затем эти группы элементов последовательно распределяются по процессам. Такая стратегия распределения
– модифицированное 2–мерное распределение данных.
Алгоритмическая совместимость – свойство распределений элементов матриц A, B и C, которое гарантирует
корректное выполнение параллельного алгоритма вычисления матричного произведения вышеописанного вида.
Определение 3 (алгоритмическая совместимость):
Матрицы A, B и C алгоритмически совместимы для параллельного вычисления матричного
произведения вида
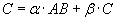тогда и только тогда, когда:
- распределение столбцов матрицы A эквивалентно распределению строк матрицы B;
- и оба распределения строк и столбцов матрицы C идентичны таковым величинам для матриц A и B соответственно.
Главная цель разработки параллельных алгоритмов перемножения матриц – независимость от распределения
данных. Данные алгоритмы не требуют определённого распределения данных, таких как: блочно–линейное
и блочно–рассеянное.
|
