Источник:
Applying the Haar Wavelet Transform to Time Series Information

     Введение

     Это первая веб-страница, которую я написал о вейвлетах. Из этого семени выросли другие страницы, на которых обсуждается множество тем, посвященных вейвлетам. Для просмотра оглавления смотрите страницу Wavelets and Signal Processing. Эта страница применяет вейвлет-преобразование к временному ряду, составленному из курса ценных бумаг на фондовом рынке. Позже веб-страницы распространили эту работу в различные сферы (например, сжатие, спектральный анализ и прогнозирование).

     Когда я начинал, я думал, что применю вейвлет Хаара, и что некоторым моим коллегам это может оказаться полезным. Я не ожидал, что обработка сигналов будет такой интересной темой. Ни понимал я и того, как много отраслей вычислительной техники, математики и количественных финансов будет затронуто вейвлетами. Я продолжал обнаруживать, что «одно ведет к другому» и очень сложно найти место логической остановки. Этот извилистый путь открытий с моей стороны стал также и причиной органического роста подобных страниц. Я пытался приручить его и систематизировать, но боюсь, что он до сих пор отражает тот факт, что я не знал куда иду, когда начинал идти.

     Java-код, опубликованный на этой, странице отражает мою первую работу над вейвлетами. Более сложные, основанные на приподнятых схемах, алгоритмы, реализованные на Java, могут быть найдены на других веб-страницах. Вейвлет код, основанный на приподнятых схемах, опубликованный на других веб-страницах, более простой и легкий для понимания. Вейвлет приподнимающие схемы предоставляют также элегантную и мощную основу для реализации множества вейвлет алгоритмов.

     При реализации пакетных вейвлет алгоритмов я переключился с Java наo C++. Пакетные вейвлет алгоритмы, которые я использовал, более просты и элегантны при использовании перегрузки операторов в C++. C++ также поддерживает структуры родового типа (шаблоны), которые позволили мне реализовать родовую иерархию классов для вейвлетов. Этот код включает в себя несколько различных вейвлет алгоритмов, в том числе Хаара, линейной интерполяции и Дебеши D4.

     Подобно вейвлет алгоритмам, финансовое моделирование, выполненное здесь, представляет собой очень раннюю работу. Когда я начинал работать над этой страницей, у меня не было опыта в моделировании финансовых временных рядов. Работа, описанная на этой странице, привела к более интенсивным экспериментам с использованием вейвлет-фильтров в финансовых моделях, которые я продолжаю разрабатывать. На этой странице я использовал курсы ценных бумаг на фондовом рынке. В финансовом моделировании обычно используются результаты выборок, на основе которых пытаются предсказать последующую выборку в будущем.

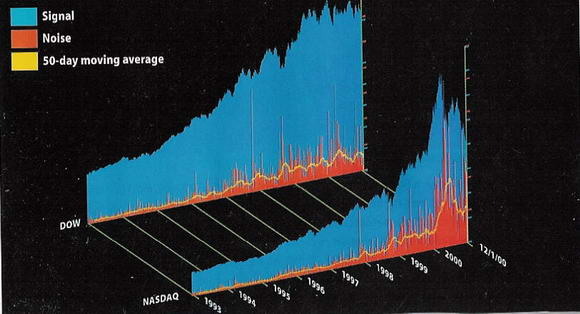
     Я заинтересовался вейвлетами случайно. Я работал над программой, связанной с финансовыми временными рядами (например, с ценами на акции), так что я предполагаю, что это была случайность, которая обязана была случиться. Я читал выпуск журнала «WIRED» от февраля 2001 года, когда увидел график, приведенный ниже. Каждый месяц «WIRED» приводили различные графики финансовых потоков, и это был один из них.

     Я платонист. Я верю, что существует абстрактная истина, но мы никогда не сможем ее достичь. Мы можем лишь добиться аппроксимации или тени истины. Современная наука выражает это в неопределенности Гайсенберга.

     Платонистический взгляд на финансовые временные ряды заключается в том, что в них истинные временные ряды искажаются до некоторого значения шумом. Например, временной ряд окончательных цен или разниц между ценой продавца и покупателя изменяется на основании предложения и спроса на акции. В случае временного ряда разниц цен кривая будет окружена шумом, создаваемым приходом случайных заказов. Если бы как-нибудь шум мог быть отфильтрован, то можно было бы увидеть истинную кривую предложения/спроса. Программа, которая использует эту информацию, могла бы работать лучше, потому что бы не учитывала ложные отклонения, вызванные шумом.

     График из журнала «WIRED», приведенный выше, предполагает, что вейвлетный анализ может быть использован для фильтрации финансовых временных рядов, чтобы удалить шум. Конечно, обширный материал не охваченный цитатой из «WIRED». Например, что порождает шум? Что такое вейвлеты и вейвлет Хаара? Почему полезно использовать вейвлеты при анализе финансовых временных рядов? Когда я увидел этот график, то не знал ответов ни на один из этих вопросов.

     Анализ, предоставленный в обзоре «WIRED» весьма поверхностный. Шум во временных рядах усиливается объемом торговли. Поскольку шум увеличился, то он должен быть нормализован для объемов торговли.

     Какое длинное и странное путешествие это было

     Чтения – опасная штука. Оно может направить вас в странных направлениях. Я переехал из Калифорнии в Санта Фе, Нью Мехико потому что я прочел книгу. Тот график в журнале «WIRED» направил меня по пути, следуя которому я провел множество месяцев. Как любой путешественник я не уверен, что встал бы на этот путь, если бы знал, насколько долгим и порою тяжелым он будет.

     Годами ранее, когда она впервые вышла, то я купил себе экземпляр книги «The World According to Wavelets» автора Barbara Hubbard, основанной на базе обзора, который я читал в журнале «Science». Книга заняла свое место на полке и стояла непрочитанной до тех пор, пока я не увидел график в «WIRED».

     Вейвлеты были чем-то вроде увлечения, модным выражением, которым разбрасывались люди. Barbara Hubbard (Барбара Губбард) начала написание «The World According to Wavelets», когда мода на вейвлеты начала разгораться. она предоставила интересную историю о том, как вейвлеты разрабатывались в мирах математики и инженерии. Она также предприняла смелую попытку объяснить, в чем же заключается техника вейвлетов. Мисс Губбард – научный писатель, но не математик, но она осилила большой объем базовых вычислений и теории обработки сигналов (за что я восхищался ею). Когда она написала «The World According to Wavelets» было лишь несколько книг, посвященных вейвлетам, и никакого вводного материала. Также я восхищаюсь героическим усилием Барбары Губбард, Я имел поверхностное понимание вейвлетов после прочтения «The World According to Wavelets».

     Существует множество литературы, касающейся вейвлетов и их применений. С точки зрения разработчика программного обеспечения (с только годом обучения в колледже) проблема с литературой по вейвлетам в том, что в большинстве своем она была написана математиками. Я не принадлежу ни к одной из этих групп, поэтому моя проблема, возможно, что я не могу быстро воспринимать язык математики. Я, конечно, чувствую это каждый раз, когда я читаю журнальные статьи по вейвлетам. Тем не менее, я пытался сконцентрироваться на книгах и статьях, которые были исключительно вводными и описательными. Даже с ними, как оказалось, мне было трудно.

     Первая глава книги « Wavelets Made Easy» автор Yves Nievergelt (Ивес Нивергельт) начиналась с объяснения вейвлетов Хаара (это вейвлеты, которые использовались для генерации графика, опубликованного в «WIRED»). Эта статья содержит множество примеров и я смог понять как применяется вейвлет Хаара из этого материала (ссфлки на мой Java-код для вейвлета Хаара приведены ниже). Следующая глава рассматривала преобразования с вейвлетом Дебеши. К сожалению, эта глава «Wavelets Made Easy» показалась мне не такой хорошей, как материал по вейвлетам Хаара. Там было множество ошибок, и применяемый Нивергельтом алгоритм не приводил к корректному вейвлет-преобразованию. Среди прочего, коэффициенты вейвлетов Дебеши были неверными. В книге «Ripples in Mathematics» описание гораздо лучше.

     Вейвлет техника для анализа сигнала или временного ряда

     Есть множество литературы по вейвлетам. Включая и тысячи статей в журналах и множество книг. Книги по вейвлетам бывают от относительно вводных как «Wavelets Made Easy» Нивергельта (которую все еще не легко читать) до книг, которые понятны лишь выпускникам-математикам. Также, огромное количество материалов есть в Интернет.

     При таком количестве литературы по вейвлетам нет необходимости в еще одном учебнике. Но может быть тяжело суммировать мои взгляды на вейвлеты в применении их к одномерным сигналам или временным рядам (изображения – двумерные сигналы). Временные ряды – это просто один из видов сигналов, запись чего-либо: температуры, уровня воды или рыночных данных (конечные цены на акции).

     Вейвлеты позволяют рассматривать временной ряд при различных разрешениях. Каждое разрешение отражает различную частоту. Техника вейвлетов определяет средние значения и разницы сигнала, раскладывая сигнал на спектр. Все вейвлет алгоритмы, с которыми я привык работать, используют значения степеней двойки (например 64, 128, 256…). Каждый шаг вейвлет-преобразования порождает два набора значений: набор средних значений и набор разниц (разницы используются как вейвлет коэффициенты). На каждом шаге получаются наборы средних и коэффициентов, каждый из которых вдвое меньше исходных данных. Например, если временной ряд содержит 256 элементов, то на первом шаге будет получено 128 средних значений и 128 коэффициентов. Средние значения после становятся входными данными для следующего шага. И так до тех пор, пока не будет вычислено единственное среднее и единственный коэффициент.

     Средние значения и разницы временных рядов рассчитываются через окно значений. Большая часть алгоритмов рассчитывают эти значения, сдвигая окно вдоль входного сигнала. Например, если входной сигнал содержит256 значений, то окно будет сдвигаться на два элемента 128 раз при расчете средних значений и разниц. На следующем шаге используются предыдущие средние значения, также сдвигая окно на два элемента. Таким образом получается эффект среднего от четырех элементов. Логически, окно умножается на два каждый раз.

     В литературе по вейвлетам этот древообразный алгоритм называется пирамидальным алгоритмом.

     Степень двойки коэффициентов спектра, сгенерированных вейвлет расчетом отражают изменения во временном ряде при различных разрешениях. Первый набор коэффициентов отражает высокочастотные изменения. Каждый последующий набор отражает все меньшие и меньшие частоты.

     Есть бесчисленное множество базовых вейвлет функций. Большая часть комплексных функций (подобно вейвлетам Дебеши) производят совмещение средних значений и разниц, предоставляя лучшие средний значения, чем вейвлет Хаара на низких разрешениях. Однако, эти алгоритмы более сложные.

     Язык вейвлетов

     Каждая сфера разрабатывает свой собственный суб-язык. Это справедливо и для вейвлетов. Я приведу несколько определений здесь, поскольку понял их значение, и это помогло мне в моих путешествиях через вейвлет литературу.

     • Вейвлет

     Функция, которая дает результат в виде набора высокочастотных разниц или вейвлет коэффициентов. В рамках приподнимающих схем вейвлет рассчитывает разницу между предсказываемым и настоящим значением.

     Если у нас значения si, si+1, si+2... вейвлет Хаара будет выглядеть следующим образом:

     Где ci – это вейвлет коэффициент.

     Вейвлет приподнимающая схема использует незначительную разницудля вейвлета Хаара:

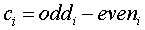
     • Масштабирующая функция

     Масштабирующая функция порождает более плавную версию набора данных, который наполовину меньше входного сигнала. Вейвлет алгоритмы рекурсивны и сглаженные данные становятся входными на следующем шаге вейвлет преобразования. Масштабирующая функция для вейвлета Хаара:

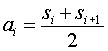
     где ai – сглаженное значение.

     Вейвлет Хаара сохраняет средние как сглаженные значения. Это справедливо не для всех вейвлет преобразований.

     • Низкочастотный фильтр

     В цифровой обработке сигналов (DSP) вейвлет – это функция низкочастотного фильтра. Низкочастотный фильтр пропускает высокочастотные компоненты сигнала, заглушая низкочастотные составляющие. Например, разницы, определенные вейвлетом Хаара представляют высокочастотные изменения между нечетным и четным значениями.

     • Высокочастотный фильтр

     В цифровой обработке сигналов масштабирующая функция – это высокочастотный фильтр. Высокочастотный фильтр заглушает высокочастотные компоненты и пропускает низкочастотные. Масштабирующая функция вейвлета Хаара рассчитывает средние значения четного и нечетного элементов, получая более гладкий низкочастотный сигнал.

     • Ортогональное преобразование

     Определение ортогонального преобразования в «Wavelet Methods for Time Series Analysis» авторы Percival and Walden, Cambridge University Press, 2000, глава 3, раздел 3.1, одно из лучших, которые я когда-либо видел. Я процитирую его ниже:

     Ортогональные преобразования интересны потому, что они могут быть использованы для такого преобразования временного ряда, что мы можем легко восстановить его из результатов преобразования. В широком смысле «информация» в преобразовании эквивалентна «информации» в оригинальном сигнале. Для обратного преобразования сигнал и его преобразование должны быть двумя продуманными представлениями одной математической сущности.

     В вейвлет преобразовании это означает, что исходный временной ряд может быть достоверно восстановлен из средних значений и коэффициентов, сгенерированных ортогональным вейвлет преобразованием.

     • Оценивание сигнала

     Это также относится к устранению шума. Алгоритмы оценивания сигнала пытаются охарактеризовать части временного ряда и удалить те, которые вписываются в модель шума.