|
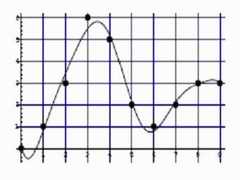
Источник:"http://www.ii.metu.edu.tr/~ion528/demo/lectures/6/2/index.html" Регистрация цифрового изображения (цифровая дискретизация, ширина полосы частот по Найквисту, эффект наложение спектров, свертка) Регистрация цифрового изображения1 Цифровая дискретизация При получении образа реальной сцены дискретизация осуществляется в два пути: выборка (дискретизация) и квантование. Рисунок 1 показывает дискретизацию и квантование одномерного сигнала в регулярной сетке. Сигнал - дискретизируется в десяти позициях (x = 0, ..., 9), и каждая дискретизируемая величина - затем отквантовывается на одном из семи уровней (y = 0, ..., 6).
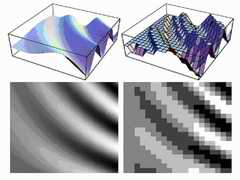
Дискретизация и квантование выполняются по одному пути, за исключением того, что дискретизация может быть выполнена в более, чем одном измерении. Пример показан на рисунке 2. Здесь, представлен непрерывный сигнал двух переменных (верхний левый), и соответствующий ему образ с сигнальной интенсивностью преобразованной в серые величины (нижняя левая). С права, показан сигнал после дискретизации в дискретной сетке и квантовании серых величин на пять уровней. ПРИМЕЧАНИЕ: в статье часто приводятся примеры, в которых цифровой образ представляется одномерным сигналом, что упрощает материал для восприятия.
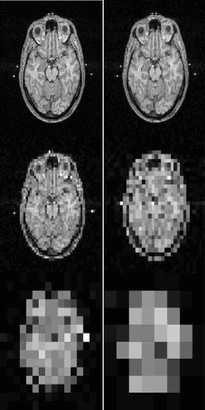
Из рисунка 2, ясно, что цифровое изображение не является достаточно хорошим представлением оригинала. Очевидно, плотность дискретной сетки и количество уровней, которые выбираются в квантовании - важные показатели качества. Эти показатели названы разрешением: пространственное разрешение равняется количеству используемых пикселей, и разрешение интенсивности, которое соответствует количеству использованных уровней серого. В цифровых представления образа, оба типа разрешения конечны. Эффект более низкого пространственного разрешения представлен на рисунке 3. Существует ещё один тип разрешения, который назван как оптическое разрешение. Оптическое разрешение - минимальная пространственная деталь, которую система визуализации может увидеть. Оптическое и пространственное разрешение часто применяются без их описания в тексте, но обязательно предопределён в контексте.
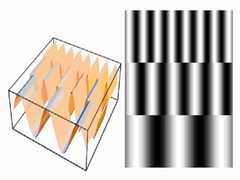
2 Ширина полосы частот по Найквисту При дискретизации изображения, можно ли получить образец идентичный оригиналу? Если это возможно, то сколько изображений необходимо? Прежде, чем ответить на эти вопросы, необходимо рассмотреть понятие пространственной частоты. Частота синусоиды определена как количество циклов (периодов), которые выполняются сигналом в единицу длины. Например, семейство функций f(x) =sin(ax) имеет частоту a/2П . Рисунок 4 показывает три синусоиды разной частоты и соответствующие им изображения. Существует связь между пространственной частотой и уровнем детализации в изображениях: высокий уровень детализации предписывается высокой частоте, и низкий уровень детализации предписывается снижению частоты. Высокий уровень детализации состоит из сравнительно резко изменяющегося контраста, то есть, интенсивность изображения быстро меняется от темного к светлому, и наоборот, что соответствует высокой частоте синусоидального сигнала. Это взаимосвязь между частотной и детализацией изображения –лежит в сердце многих изображений, и будет именоваться в дальнейшем как Фурье - преобразование.
Как отмечалось ранее, в цифровом изображении, пространственное разрешение и разрешение интенсивности конечны. Следовательно, прекрасное представление деталей изображения может быть ограничено, как и ограничен диапазон пространственных частот, наблюдающийся в подлинном изображении. Это подразумевает, что количество образов, которые требуются изображению для точного воспроизведения всех деталей, также конечны. Это наблюдение относительно пространственной частоты связано с теоремой дискретизации: «Для того, чтобы захватывать самые верхние частоты (то есть, самые маленькие детали) непрерывного изображения, частота дискретизации должна быть ПРИМЕЧАНИЕ: во многих книгах применяется термин "полоса" при обсуждении частоты. Если частота имеет ограниченный диапазон, она называется полоса частот. Диапазон частоты называется - ширина полосы частот. Если дискретизация изображения выбрана ниже ширины полосы частот по Найквисту, детали будут потеряны. Дискретизация с повышенной частотой, с другой стороны, не увеличит уровень детализации: все детали уже были захвачены, когда дискретизация осуществлялась точно на ширине полосы частот по Найквисту. Пример: рассматривается следующая линия, взятая из изображения.
Образец имеет частоту 1/2 за пиксель -то есть, есть 2 пикселя в образце повторяют ширину полосы частот по Найквисту как
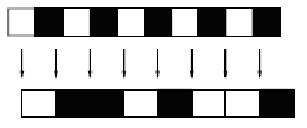
Если уменьшить частоту дискретизации до 1/3 за пиксель, то полученный образ будут иметь детали отсутствовавшие в подлинном изображении:
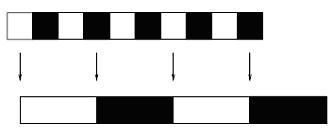
3 Эффект наложение спектров Феномен, происходящий в конце выше указанного примера назван как эффект наложения спектров: если изображение дискретизированно при показателе ниже половины, указанной ширины полосы частот по Найквисту, то высокая частота, формируемая в подлинном изображении преобразуется к более низкой частоте, чтобы уменьшает частотные представления изображения. Из выше указанного примера видно, что образец с частотой 1/2 за пиксель отображается в с частотой 1/6 за пиксель. Пример: рисунок 8 показывает другой пример эффекта наложения спектров.
Дискретизируя функцию f(x; y) = 4 Дискретизация и свертка До этого момента предполагалось, что возможно дискретизировать изображение с бесконечной точностью. На практике это - невозможно, поскольку практическое формирование изображений устройствами не может иметь бесконечную точность. Например: если используется камера для получения изображений с некоторой бесконечно небольшой позиции (x,y), то камера соберет эти образы изображения в небольшом районе вокруг (x,y). На самом деле существует другая причина почему дискретизация с бесконечной точностью невозможна: камерам нужна энергия от поступающих световых лучей, чтобы обнаруживать эти лучи. Даже, если возможно настроить камеру на бесконечную точность только для бесконечно небольших точек (x,y), то энергия от поступающих световых лучей должна быть уменьшена до нуля. То в этом случае ничего не будет обнаружено. Выбор оптимальных соотношений: с одной стороны, необходимо сделать дискретизацию по возможности чёткой, чтобы дискретизировать небольшую область, но с другой стороны, дискретная область не может быть слишком маленькой, или это не выделит достаточно энергии для соответствующего обнаружения. ВверхИсточник:"http://www.ii.metu.edu.tr/~ion528/demo/lectures/6/2/index.html" Digital image acquisition (sampling, quantization, color models) |
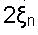 или больше, где
или больше, где 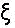 равняется самой верхней частоте, наблюдающегося в оригинальном изображении.
равняется самой верхней частоте, наблюдающегося в оригинальном изображении. 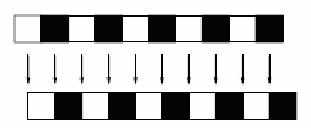

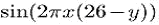 в основной области
в основной области 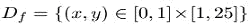 в которой происходит снижение частоты, как было показано при перемещении от верхней линии к самой нижней: частота 25 за пиксель - верхняя линия, и частота 1 за пиксель - нижняя линия. Функция была дискретизирована четыре раза используя и другие частоты дискретизации. Эффект наложения спектров на самой низкой дискретной частоте такой сильный, что высокие частоты изображеные на верхнем образце отображаются на тех же частотах низкого уровня на образце, расположенном ниже.
в которой происходит снижение частоты, как было показано при перемещении от верхней линии к самой нижней: частота 25 за пиксель - верхняя линия, и частота 1 за пиксель - нижняя линия. Функция была дискретизирована четыре раза используя и другие частоты дискретизации. Эффект наложения спектров на самой низкой дискретной частоте такой сильный, что высокие частоты изображеные на верхнем образце отображаются на тех же частотах низкого уровня на образце, расположенном ниже.