 C ИСПОЛЬЗОВАНИЕМ СНИЖЕНИЯ ГРАФА
C ИСПОЛЬЗОВАНИЕМ СНИЖЕНИЯ ГРАФА
(Efficiently Solving Dynamic Markov Random Fields using Graph Cuts )
Перевод: А.В. Панкова
| Библиотека | Реферат | Ссылки | Отчет о поиске | Индивидуальное задание |
ЭФФЕКТИВНОЕ РЕШЕНИЕ ДИНАМИЧЕСКИХ МАРКОВСКИХ СЛУЧАЙНЫХ ПОЛЕЙ C ИСПОЛЬЗОВАНИЕМ СНИЖЕНИЯ ГРАФА
C ИСПОЛЬЗОВАНИЕМ СНИЖЕНИЯ ГРАФА
(Efficiently Solving Dynamic Markov Random Fields using Graph Cuts )
Перевод: А.В. Панкова
Pushmeet Kohli Philip H.S. Torr
Department of Computing
Oxford Brookes
University
{fpushmeet.kohli,philiptorrg}@brookes.ac.uk
http://cms.brookes.ac.uk/computervision
Резюме
В этой статье представлен новый, быстрый, полностью динамический алгоритм для решения "st-mincut"/"max-flow" задач. Показывается, как этот алгоритм может быть использован, для эффективного вычисления оценки МАР динамического изменения выделенных моделей МСП в компьютерном зрении, типа сегментация изображения. Учитывая решение задачи "max-flow" в графе, показывается, как эффективно вычислить максимальный поток в измененной версии графа. Эксперименты показывают, что время, которое необходимо алгоритму, приблизительно пропорционально числу граней, вес которых различен в двух графах. Выполнение алгоритма тестируется на конкретной задаче: задача сегментации фонового объекта для видео и сравнение его с наилучшим известным "st-mincut" алгоритмом. Результаты показывают, что динамический граф сокращает алгоритм значительно быстрее чем его статический аналог и позволяет сегментировать изображение в реальном времени. Необходимо отметить, что приведенный метод обобщенный и может использоваться для усовершенствования в других случаях, когда применяется динамическое изменение графа.
1. Введение
Снижение графа часто используется в машинном зрении как техника минимизации энергии. Одна из первых причин роста популярности - наличие многочисленных алгоритмов с превосходной алгоритмической сложностью для решения "st-mincut" задачи [1]. Грейг и другие [11] показали, что точное "maximum a-posteriori" (максимум по опыту - МАР) решение для двух отмеченных пар Марковских случайных полей (МСП) может быть получено в полиномиальное время путем обнаружения "st-mincut" на эквиалентном графе. Эквивалентность между "st-mincut" задачей и оценкой МАР-МСП делает снижение графа чрезвычайно важным, особенно учитывая то, что вероятность распределения взаимодействующих меток во многих задачах, таких как, например, сегментация изображения, стерео, восстановление изображения, могут быть смоделированы с использованием МСП. Также показано, что прочный локальный оптимум MСП введеный Поттсом, и модели линейных кликов потенциалов могут быть получены при использовании снижения графа [5].
Учитывая решение МСП, возникает вопрос относительно того, может ли это решение помогать в решении другого подобного МСП со слегка различными энергетичекими условиями. Например, дело обстоит так, когда сегментация изображения выполняется в рамках видео, где задача состоит в изменении данных (изображения) от одного момента времени к следующему. Решение МАР для МПС представляет, что задача в предыдущий момент должна интуитивно быть хорошей инициализацией для процедуры минимизации энергии. Если изменение МСП относительно небольшое от одного момента времени к следующему, то такая инициализация должна в значительной степени ускорить процесс логического вывода, начиная со времени, необходимого для поиска нового решения, которое должно быть пропорционально изменению функции энергии. В пределах этой статьи показывается, что для "st-mincut"/"max-flow" задач это соответствует использованию потоков, полученных при решении предыдущего вида задач, и обнаружению решения следующего вида задачи, как показано на Рис.1.

Рис.1. Динамическая сегментация изображения, при использовании Снижения Графа. Изображения в первой колонке - два последовательных кадра видеопоследовательности и их соответствующая сегментация, на первом изображении показывается использование зерна сегментации (которое используется как мягкое ограничение на сегментацию). В колонке 2 наблюдаются полученные потоки n-границ, соответствующие МАР решению МСП представления этих двух задач. Может быть отмечено, что потоки, соответствующие этим сегментациям, подобны. Потоки из первой сегментации использовались для обнаружения сегментации для второго кадра. Времени для выполнения этой процедуры было затрачено намного меньше в сравнении с временем, затраченным на обнаружение временных потоков.
Такой алгоритм для "max-flow" задачи должен принадлежать к широкой категории алгоритмов, которые упомянуты как динамические. Эти алгоритмы решают задачу, динамически обновляя решение предыдущего значения задачи. Их цель состоит в том, чтобы получитть более эффективное вновь вычисленное решение задачи после каждого временного изменения. Данный ориентированный взвешенный граф полностью динамического алгоритма должен учитывать возможность неограниченной модификации графа.
Снижение Графа в Машинном Зрении Выбрано включение динамической информации в снижения графа (в других алгоритмах логического вывода распространению подобное убеждение) из-за того, что снижение графа обеспечивает точное, глобальное, оптимальное решение некоторых энергетических функций. Они использовались, чтобы получить превосходные результаты для множества задач машинного зрения и полный анализ их применимости был выполнен исследователями. Колмогоров и Забих [14] ] определили набор энергетических функций, которые могли бы быть минимизированы при использовании снижения графа, обеспечивая некоторые условия, которые должны быть удовлетворены всеми такими функциями. Бойков и другие [6] предложили алгоритмы, основанные на снижении графа, которые могли эффективно находить приближенные решения различных функций энергии. Множество статей также обращались к теоретическим свойствам построения графов, которые использовались в машинном зрении. Эти свойства влияют на эффективность алгоритмов, которые решают "st-mincut" задачу. Бойков и другие [4] предложили специализированный алгоритм для "st-mincut" обнаружения, который экспериментально показал, что является более быстрым на графах, обычно используемых в приложениях зрения, по сравнению с другими алгоритмами, используемыми для решения этой задачи.
Краткий Обзор Динамического Снижения Графа Динамические алгоритмы не новы в машинном зрении. Они широко использовались в вычислительной геометрии для задач типа поиска диапазона, пересечений, местоположения точки и многих других. О большинстве динамических алгоритмов, используемых в вычислительной геометрии, можно прочитать в [7].
Множество алгоритмов было предложено для динамической обобщенной "mincut" задачи. Соруп [16] предложил метод, который имел дополнительное изменение времени O(|E|1/2) и выбирал граничное время O(log n), чтобы внести в список грани снижения.
Бойков и Жолли [3] были первыми, кто использовали частично динамический "st-mincut" алгоритм в приложении машинного зрения, предлагая технику, с которой они могли бы корректировать способности некоторых граней графа, и повторно динамически вычислять "st-mincut". Они использовали этот метод для выполнения интерактивной сегментации изображения, в которой пользователь мог улучшать результаты сегментации, применяя дополнительную сегментацию зерен диалоговым способом. Тем не менее, их схема была ограниченной и не позволяла изменять граф полностью. Объяснение этого ограничения в контексте динамического МСП приведено в статье позже.
Организация Статьи В этой статье представлен новый, полностью динамический алгоритм для задачи "st-mincut", который учитывает произвольные изменения в графе. Показывается, как этот алгоритм может использоваться, чтобы динамически выполнять логический МАР вывод в МСП. Такая процедура вывода чрезвычайно быстрая и может использоваться во множестве задач.
Раздел 2 представляет краткий обзор "st-mincut"/"maxflow" задачи. В разделе 3 обсуждается МСП и показывается, как они используются в модели выделенной задачи подобно сегментации изображения и стерео, и как могут быть найдены МАР оценки для МСП с использованием снижения графа. В разделе 4 показывается, как МАР решения могут быть эффективно вычислены для динамического изменения МСП при обновлении структуры данных, используемых для решения "maxflow" задачи. Подробно описывается, как преобразовывается остаточный граф, чтобы отразить изменения в первоначальном графе, и обсуждаются проблемы, связанные с вычислительной сложностью динамического алгоритма. В разделе 5 описывается, как процесс перевычисления "st-mincut"/"maxflow" может быть далее оптимизирован при использовании прошедших повторную обработку деревьев поиска. В разделе 6, используется динамический алгоритм для выполнения сегментации изображения в видео последовательностях, и сравнивается его выполнение с таким же "st-mincut" алгоритмом, описанным в [4].
2. Предварительные сведения
В этом разделе проводится общий краткий обзор "st-mincut"/"maxflow" задачи, и даны примечания, используемые в статье. Ориентированный взвешенный граф G(V; E; C) с неотрицательным весом граней определен набором узлов V, набором ориентированных границ E, и стоимостью граничной функции C, определенной как:
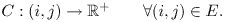 |
(1) |
Далее n и m обозначают номера узлов |V| и номера граней |E| в графе соответственно.
Графы, используемые в "st-mincut" задаче имеют некоторые специальные узлы,
называемые предельными узлами, а именно источник s и выход t.
Грани в графе могут быть разделены на две непересекающиеся категории:
t-грани, которые соединяют узел с предельным узлом,
и n-грани, которые соединяют узлы, кроме предельных узлов, друг с другом.
Мы делаем следующие предположения в нашем примечании:
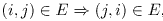 и
и 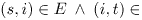 для всех
для всех
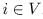 .
Эти предположения не ограничивающие, поскольку грани с нулевыми весами граней допускаются в нашей формулировке.
Таким образом мы можем придерживаться нашего примечания без изменения задачи.
.
Эти предположения не ограничивающие, поскольку грани с нулевыми весами граней допускаются в нашей формулировке.
Таким образом мы можем придерживаться нашего примечания без изменения задачи.
Определение 1
Снижение - разделение установленного узла V на две части S и 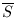 =V - S,
определено набором граней (i,j), таких, что i
=V - S,
определено набором граней (i,j), таких, что i  S и j
S и j 
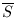 .
Стоимость снижения (S,
.
Стоимость снижения (S,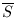 ) равна:
) равна:  .
"St-cut" - снижение, удовлетворяющее свойствам: s
.
"St-cut" - снижение, удовлетворяющее свойствам: s  S и t
S и t 
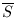 .
.
Учитывая ориентированный взвешенный граф G, задача "st-mincut" состоит в обнаружении "St-cut" с минимальной стоимостью. По теореме Форд-Фулкерсона [10], это эквивалентно вычислению максимального потока от источника до выхода, с емкостью каждой грани, равной cij [1].
2.1. Формулировка Задачи "max-flow"
Для сети G(V; E) с неотрицательной емкостью cij, связанной с каждой гранью, задача "max-flow" состоит в обнаружении максимального потока f от начального узла s до конечного узла t, подчиненного емкости грани и ограничении массы баланса:
 |
(2) | |
 |
(3) |
где fij поток от узла i к узлу j, lij более низкая граница в потоке fij(которая в нашем случае равна нулю) и N(x) - состоящий из всех узлов, соединенных гранями с x. Обратите внимание, здесь можно инициализировать потоки в t-гранях как fsx=fxt=min(csx;cxt). Это соответствует продвижению потока по пути с наименьшим увеличением (определенным позже) от источника до выхода. Остаточные емкости предельных граней таким образом станут:
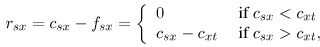 |
and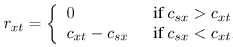 |
Отметим, что решение задачи максимального потока инвариантно абсолютному значению предельных емкостей граней csx и ctx. Это зависит только от различия этих емкостей (ctx - csx). Добавление или вычитание константы к этим емкостям заменяет объективную функцию константой и не выполняет полного решения. Это свойство задачи будет использоваться позже для обновления остаточного графа, когда первоначальный граф был изменен.
2.2. Увеличение Пути и Остаточные Графы
Данный поток fij, остаточная емкость rij
грани (i; j)  E - максимальный дополнительный поток,
который может быть послан от узла i к узлу j используя грани (i; j) и (j; i).
Остаточная емкость rij имеет два компонента: неиспользованная емкость грани
(i; j): cij - fij, и текущий поток fij от узла
j к узлу i, который может быть уменьшен для увеличения потока от i к j.
E - максимальный дополнительный поток,
который может быть послан от узла i к узлу j используя грани (i; j) и (j; i).
Остаточная емкость rij имеет два компонента: неиспользованная емкость грани
(i; j): cij - fij, и текущий поток fij от узла
j к узлу i, который может быть уменьшен для увеличения потока от i к j.
Определение 2 Остаточный граф G(f) взвешенного графа G состоит из узла установившего V и грани с положительной остаточной емкостью (относитьно потока f).
Топология G(f) идентична G. G(f) отличается только емкостью своих граней. Для потока f = {0}, G(f) такое, как G.
Определение 3 Увеличивающийся путь - путь от источника до выхода по ненасыщенным граням остаточного графа.
Алгоритмы для решения задачи "max-flow" могут быть классифицированы по двум категориям: Увеличение Пути и Алгоритмы Предпотокового Толчка. Алгоритмы увеличения пути многократно находят увеличение путей в остаточном графе G(f) и толкает максимально возможный поток f' по пути, который заканчивается общим потоком (f + f') и остаточным графом G(f + f'). Алгоритмы предпотокового толчка перполняют сеть и создают избыточный поток в узлах графа. Затем этот избыточный поток пошагово уменьшается и посылается к выходу или источнику.
3. Марковские Случайные Поля
Рассмотривается набор случайных переменных X =
{ X1,X2,...,Xn}
определенных в наборе S, таких, что каждая переменная Xi
может принимать значение xi из набора L ={ l1,l2,...,ln}
всех возможных значений.
Затем говорят, что Х является МСП относительно системы
N = { Ni| i  S}
если, и только если безусловно удовлетворяется свойство P(x)>0 и
Марковское свойство P(xi|xS-{i}) = P(xi|xNi ),
S}
если, и только если безусловно удовлетворяется свойство P(x)>0 и
Марковское свойство P(xi|xS-{i}) = P(xi|xNi ), 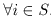 .
Здесь сслылаемся на преобразование Pr(X = x) к P(x), Pr(Xi=xi) к P(xi),
и совместного случая (X1 = x1,...,Xn = xn) к
X = x , где x = { xi| i
.
Здесь сслылаемся на преобразование Pr(X = x) к P(x), Pr(Xi=xi) к P(xi),
и совместного случая (X1 = x1,...,Xn = xn) к
X = x , где x = { xi| i  S} конфигурация X, которая
соответствует реализуемому полю.
S} конфигурация X, которая
соответствует реализуемому полю.
Оценка MAP-МСП может быть сформулирована как задача минимизации энергии, где энергия соответствующей конфигурации x - отрицательный логарифм вероятности, граничащей со следующей вероятностью МСП, и определеной как
E(x)= - log Pr(x|D).
3.1. МСП для Сегментации Изображения
В контексте сегментации изображения, S соответствует набору пикселей всего изображения, N - окрестность, определенная на этом наборе, набор L включает метки, представляющие различные сегменты изображения, и случайные переменные в набореX обозначают отмеченные пиксели на изображении. Отметим, что каждая конфигурация x МСП определяет сегментацию. Задача сегментации изображения может быть решена путем обнаружения наименьшей энергии конфигурации МСП. Энергия, соответствующая конфигурации x, состоит из вероятности и предшествующего терма:
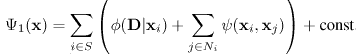 |
(5) |
где 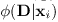 логарифм вероятности,
который налагает индивидуальный штраф за назначение метки li на пиксел i
и определяется как:
логарифм вероятности,
который налагает индивидуальный штраф за назначение метки li на пиксел i
и определяется как:
 если xi=lk если xi=lk |
(6) |
где Hk - распределение RGB для Sk,
сегмент, обозначенный меткой - lk. Здесь
Pr( i  Sk | Hk )=Pr( Ii | Hk ), где
Ii интенсивность цвета пикселя i. Предшествующий
Sk | Hk )=Pr( Ii | Hk ), где
Ii интенсивность цвета пикселя i. Предшествующий
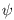 (xi,xj) принимает форму Обобщенной Модели Поттса.
(xi,xj) принимает форму Обобщенной Модели Поттса.
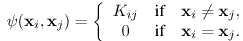 |
(7) |
В МСП для сегментации изображения используют условие добавления контраста, который полезен для пикселя с подобным цветом и имеющего ту же метку [2, 3, 15]. Это включено в энергетическию функцию для сокращения стоимости в пределах модели Поттса для двух меток, являющихся различными пропорционально различию в их интенсивности передачи пикселя. Например, для экспериментов, упомянутых в разделе 6, мы используем выражение:
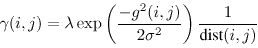 |
(8) |
где g2(i; j) измеряет различие в значениях RGB пикселей i и j, (i; j) представляет пространственное расстояние между i и j. Этот терм не может быть включен в предыдущий, так как предыдущий не может добавлять данные и, следовательно, должен быть добавлен отдельно [15]. Функция энергии МСП теперь перепишется так:
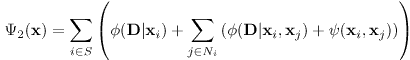 |
(9) |
Условие контраста функции энергии определено так:
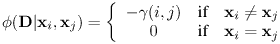 |
(10) |
3.2. Динамические Марковские Случайные Поля
Отметим, что энергия МСП, определенная ранее для сегментации изображения, зависит от данных (интенсивности цвета пикселей) и параметров, используемых в функции энергии. Это также остается действительным для МСП моделирования задачи маркировки стерео, где метка, которую необходимо оценивать для каждого участка (пикселя) МСП, является неравенством конфигурации xp. При выполнении сегментации изображения в видеопоследовательностях, функция энергии МСП изменяется с каждой структурой изображения. Рассмотрим такой вид МСП как динамический. Задача стерео в контексте видео может быть смоделирована с использованием динамических МСП подобным способом [13]. Ключевой вклад этой статьи - динамический алгоритм "max-flow", с которым решение динамического МСП может быть эффективно вычислено при использовании решения его предыдущего состояния, как показано на Рис.1.
3.3. Решение МСП при Использовании Снижения Графа
Конфигурация х в МСП имеет меньшее энергии соответствия
МАР решению МСП.
Минимизация энергии, как например, определенная в (9), может быть выполнена
вычислением снижения графа [5].
Далее глобальные минимумы функции энергии могут быть вычислены точно для пар МСП
с выпуклыми парами термов, нахождением "st-mincut" на эквивалентном графе [11, 12].
Теперь описывается эквивалентное построение графа для двухметочного случая,
для многометочного случая - обратится к [12].
Каждая случайная переменная Xi МСП представлена вершиной
vi в графе, который соединен через n-грани к соседним
определенно установленным вершинам: { vk | Xk
 Ni}. Стоимость n-грани (i; j),
соединяющей грани vi и vj, определяется:
Ni}. Стоимость n-грани (i; j),
соединяющей грани vi и vj, определяется:  .
.
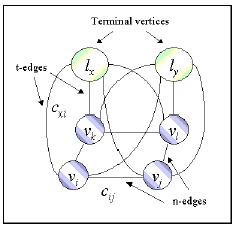
Рис.2: Граф, представляющий МСП с двумя метками
lx и ly, и четырьмя случайными переменными
xi, xj, xk и xl.
Стоймость t-грани cxi:  , и n-грани cij:
, и n-грани cij:
 .
.
Две метки lx и ly представлены специальными вершинами:
источником s и выходом t. Они соединяют все остальные вершины представления
скрытых переменных в МСП t-гранями. Стоимость t-грани определена через вероятность
терма 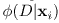 функции энергии МСП.
"St-cut" в этом графе, который отделяет источник и выход,
определяет конфигурацию x МСП, и стоимость снижения - энергию x [5].
Из этой эквивалентности, вычисляя минимальную стоимость снижения, можно найти
МАР-решение МСП.
функции энергии МСП.
"St-cut" в этом графе, который отделяет источник и выход,
определяет конфигурацию x МСП, и стоимость снижения - энергию x [5].
Из этой эквивалентности, вычисляя минимальную стоимость снижения, можно найти
МАР-решение МСП.
4. Оценка MAP-решения для Динамических МСП
Показав, как любая функция энергии, определяемая парами МСП может быть точно минимизирована для решения "st-mincut"/"maxflow" задачи, теперь показывается, как это решение может использоваться, чтобы эффективно решать любую подобную функцию энергии. Рассматриваются два МСП Ma и Mb, функции энергии которых соответсвенно Ea и Eb различны в нескольких термах. Предположим, что найдено решение МАР - Ma путем решения задачи "max-flow" на графе Ga с представлением энергии Ea, и теперь необходимо найти решение Mb. Отметим, что представление графа Eb, т.е. Gb отличается от Ga несколькими стоимостями граней. Вместо перевычисления "max-flow" на Gb на пустом месте, мы динамически модернизируем потоки, полученные при решении Ea, включая различия между Ga и Gb в остаточном графе, полученном из "max-flow" решения Ga. В этом процессе можно сохранить поток от источника до выхода, на который не влияют различия в емкости (стоимости) граней Ga и Gb. После обновления потоков и остаточных емкостей граней, алгоритм "max-flow" повторно перезапускается на остаточном графе.
Бойков и Жолли [3] в своей работе при интерактивной сегментации изображения использовали эту технику для эффективного нового вычисления МАР решения, когда вероятность терма (6) изменяется (из-за дополнения новых жестких и мягких ограничений пользователем). Однако, их техника имела ограничения и могла обращаться только с изменениями в стоимости t-граней графа. Новый метод может обращаться с произвольными изменениями в графе. В экспериментах использовался подход эффективного повторного вычисления МАР-решения для сегментации изображения в видео. Обращаем внимание, что изменение изображения заканчивается изменениями обоих вероятностей и противоположных термов функции энергии.
4.1. Обновление Остаточного Графа
При изменении остаточного графа некоторые потоки могут нарушить новые ограничения свойств граней. Теперь показано, как остаточный граф преобразован, чтобы делать такие потоки последовательными. Рассмотрим задачи обновления емкостей граней для n-граней и t-граней отдельно.
4.1.1 Модификация емкости n-граней
Рассмотрим, как обновить остаточный граф при изменении емкости n-грани. Используется c'i,j чтобы обратиться к новой емкости грани, и r'i,j и f'i,j, чтобы представить обновленную остаточную емкость и, соответственно, поток для грани (i; j). Учитывается, что обновление емкости грани в остаточном графе типично, если новая емкость грани c'i,j больше или равна старой емкости грани r'i,j. Обновленная остаточная емкость r'i,j получена так:
| r'i,j=ri,j+ (c'i,j - ci,j) | (11) |
Даже если c'i,j меньше чем ci,j , процедура все еще остается типичной, если поток fi,j меньше, чем новая емкость грани c'i,j. Это является следствием того, что уменьшение емкости грани не влияет на согласованность потока сети, т.е. поток fi,j удовлетворяет ограничению емкости грани (2) для новой емкости грани. Остаточная емкость грани может обновляться согласно уравнению (11). Различие в этом случае в том, что (c'i,j - ci,j) отрицательна и следовательно закончится уменьшением остаточной емкости. В обоих эти случаях поток через грань остается неизменным, т.е. (f'i,j = fi,j).
Задача перестает быть типичной в случае, когда новая емкость грани c'i,j меньше, чем поток fi,j. В этом случае fi,j нарушает ограничение емкости грани (2). Чтобы сделать fi,j последовательным, необходимо отказаться от избыточного потока (fi,j - c'i,j) от грани (i; j).
Показывается, как решить эту несогласованность в константе, т.е. во время O(1). Мы устанавливаем значение потока грани, равное новой емкости грани, т.е. f'i,j=c'i,j. Это изменение значения потока изменяет остаточную емкость граней (i; j) и (i; j) так: ri,j=c'i,j - f'i,j = 0 и r'i,j=ci,j + f'i,j. Далее, это изменение в потоке по грани (i; j) создает избыток si потока в узле i и недостаток dj потока в узле j, что нарушает ограничение массы баланса (3) для узла i и узла j, где si = dj = fi,j - f'i,j = fi,j - c'i,j.
Удовлетворение Массовых Ограничений Баланса Массовое ограничение баланса для узла i после обновления потоков становится:
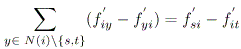 |
(12) |
Хранение потока всех n-граней кроме грани (i; j) такое же, т.е.
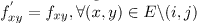 и вычитая уравнение (12) из (3), мы получим:
f'si =f'it= fsi-fit-si.
Устанавливая f'si= fsi, получаем
f'it= fit+si.
Аналогично, для узла j получим f'sj= fsj+dj.
и вычитая уравнение (12) из (3), мы получим:
f'si =f'it= fsi-fit-si.
Устанавливая f'si= fsi, получаем
f'it= fit+si.
Аналогично, для узла j получим f'sj= fsj+dj.
Теперь сосредоточимся на массовом ограничении баланса узла i (для узлаj,
процесс будет аналогичен). Новое значение потока от узла i к конечному узлу t,
f'it удовлетворяет массовому ограничению баланса для узла i
и в действительности решает задачу. Однако, проблема возникает,
если новое значение потока нарушает ограничение емкости грани для грани (i; t) т.е.
f'it >cit.
Чтобы преодолеть эту проблему, добавляется константа  к емкостям обоих граней (i; t) и (s; i), получается:
c'it and c'si соответственно,
где
к емкостям обоих граней (i; t) и (s; i), получается:
c'it and c'si соответственно,
где  = max {0, f'it - cit },
или
= max {0, f'it - cit },
или  = max {0, (fit + si) - cit },
или
= max {0, (fit + si) - cit },
или  = max {0, si - rit }.
Это преобразование заменяет объективное значение функции на постоянное и, следовательно,
не изменяет оптимальное решение.
Эта константа может быть записана отдельно, и игнорироваться при решении задачи.
Остаточные емкости этих граней переписываются так:
= max {0, si - rit }.
Это преобразование заменяет объективное значение функции на постоянное и, следовательно,
не изменяет оптимальное решение.
Эта константа может быть записана отдельно, и игнорироваться при решении задачи.
Остаточные емкости этих граней переписываются так:
r'si =(csi +  ) -
f'si ) -
f'si |
(13) |
и
r'it =(cit +  ) -
f'it ) -
f'it |
(14) |
Заменив  в (13,14) и упростив, получаем:
в (13,14) и упростив, получаем:
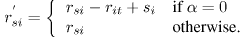
и
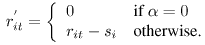
Аналогично для узла j, получим:

и
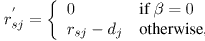
where 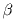 =
max{0, f'sj - csj }.
Шаги обновления остаточного графа, в случае, когда обновленная емкость грани
c'ij, меньше чем поток fij, показываются на Рис.3.
=
max{0, f'sj - csj }.
Шаги обновления остаточного графа, в случае, когда обновленная емкость грани
c'ij, меньше чем поток fij, показываются на Рис.3.
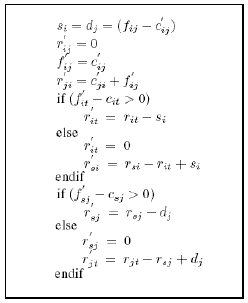
Рисунок 3: Алгоритм обновления остаточного графа в случае, когда обновленная емкость грани c'ij, меньше чем поток fij
4.1.2 Модификация емкости t-граней
Метод для обновления предельных граней подобен тем, которые используются в [3].
Мы пропускаем типичные случаи, где поток fsi - меньше, чем обновленная емкость грани
c'si, и непосредственно рассматриваем случай, когда поток больший,
чем обновленная емкость грани и, следовательно, нарушается ограничение емкости грани (2).
Поток делается последовательным с помощью константы  =fsi - c'si
добавленной к обоим t-граням, которые связанны с узлом i.
Такое изменение не влияет на решение "st-mincut" задачи, как объяснено ранее.
Остаточные емкости вычисляются так: r'si
= c'si - fsi +
=fsi - c'si
добавленной к обоим t-граням, которые связанны с узлом i.
Такое изменение не влияет на решение "st-mincut" задачи, как объяснено ранее.
Остаточные емкости вычисляются так: r'si
= c'si - fsi +  = 0
и r'it = cit - fit +
= 0
и r'it = cit - fit +  ,
или r'it = rit - c'si + fsi.
,
или r'it = rit - c'si + fsi.
4.2. Анализ Сложности Управления Обновлением
Изменение стоимости грани в остаточном графе требует постоянного времени. Произвольные изменения в графе, подобно дополнению или удалению узлов и граней, могут быть выражены в термах изменения стоимости грани. Временная сложность всех таких изменений - O (1), кроме удаления узла, где обновленное время это O(k ), где k - степень узла, который будет удален.
После того как остаточный граф был обновлен, чтобы отразить изменения в МСП, начинается общая процедура увеличения пути для того, чтобы найти максимальный поток. Процедура включает неоднократное обнаружение увеличение путей в остаточном графе и их насыщение. Когда увеличение пути больше не может быть выполнено, т.е. источник и выход разъединены в остаточном графе, достигается максимальный поток.
Максимальный поток от источника до выхода - свободная верхняя граница в числе
увеличивающихся путей, находится в соответствии с процедурой увеличения пути.
Полное изменение емкости грани ограничивает увеличение в потоке 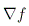 ,
определенном как:
,
определенном как:
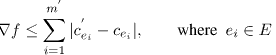 |
или 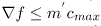 , где
cmax = max( |c'ei-cei| ).
Т.о. получено типичное O(m 'cmax ), связанное с количеством увеличений, где
m ' - количество обновленных емкостей граней.
, где
cmax = max( |c'ei-cei| ).
Т.о. получено типичное O(m 'cmax ), связанное с количеством увеличений, где
m ' - количество обновленных емкостей граней.
5. Оптимизирующий Алгоритм
Ранее было рассмотрено динамическое обновление остаточного графа и уменьшение необходимого для вычисления "st-mincut" времени. Далее можно улучшить время выполнения, используя технику активного увеличения пути, основанную на алгоритме, предложенном в [4] для решения "st-mincut"/"max-flow" задачи. Например, Диник [9] предложил алгоритм увеличения пути, который формирует деревья поиска для обнаружения увеличения пути. В вычислительном отношении это избыточная операция, так как необходимо посещать почти все узлы графа, что делает алгоритм медленным, если необходимо осуществлять обнаружение увеличения пути слишком часто. Бойков и другие [4] предложили алгоритм, в котором многократно используется дерево поиска. Экспериментально этот алгоритм оказался лучше чем алгоритм Увеличения Пути, который обычно используется в компьютерном зрении.
В представленном динамическом "max-flow" алгоритме повторно используется дерево поиска, полученное при предыдущем вычислении "max-flow", чтобы найти решение в обновленном остаточном графе. Эта техника сохраняет стоимость создания нового дерева поиска, т.о. существенно ускоряется процесс выполнения алгоритма .
5.1. Многократное Использование Деревьев Поиска
Алгоритм поддерживает два неперекрывающихся дерева поиска S и T с корнями в источнике s и выходе t соответственно. Дерево S все грани от каждого родительского узла до его потомка не насыщаются, в то время как в дереве T не насыщаются грани от потомков к родителям. Узлы, которые не включены в дерево S или T, называются свободными. Узлы в деревьях поиска S и T могут быть или активными (могут расти путем приобретения новых потомков по ненасыщаемым граням) или пассивными. Когда активный узел входит в контакт с узлом другого дерева, увеличивающийся путть найден. Алгоритм имеет три основных стадии:
Стадия Роста: Деревья поиска S и T растут до тех пор, пока они не достигнут результата в увеличении пути. Активные узлы исследуют смежные ненасыщаемые грани и приобретают новых потомков из набора свободных узлов, которые теперь становятся активными. Как только все соседи данного активного узла исследуются, активный узел становится пассивным.
Стадия Увеличения:: Поток отправляется по найденом в стадии роста пути. В результате некоторые узлы деревьев S и T становятся сиротами, так как грани, связывающие их с родителями станут насыщаемыми. Отметим, что это нарушает источник и выход деревьев поиска в лесу.
Стадия Принятия: Деревья поиска восстанавливаются при нахождении нового родителя (того же набора через не-насыщаемую грань) для каждой сироты. Если никакой квалифицированный родитель не может быть найден, узел становится свободным.
При динамическом обновлении остаточного графа, некоторые грани деревьев S и T могут стать насыщенными. Эти грани должны быть удалены. Деревья в лесу ломаются и делают некоторые узлы сиротами. Отслеживаются все осиротевшие узлы, и перед перевычислением "st-mincut" на измененном остаточном графе восстанавливаются деревья, находя нового, правильного родителя для каждого узла.
6. Экспериментальный Анализ
Представлено выполнение метода, используя задачу сегментации фона объекта. Отметим, что алгоритм иллюстрируется на задаче сегментации видео для простоты демонстрации.
6.1. Быстрая Сегментация Изображения в Видео
В задаче сегментации фона объекта необходимо исключить объекты на изображении так, чтобы они могли использоваться в другом контексте [3]. Для приведенного примера этот процесс должен быть выполнен по всем кадрам видеопоследовательности. Задача сформулирована следующим образом.
Пользователь определяет жесткие и мягкие ограничения для сегментации,
обеспечивая сегментацию реплики или зерна. Мягкие ограничения используются,
чтобы построить гистограмму цветов для объекта и фона,
которую используют для вычисления вероятности терма  функции энергии (9)
МСП [3]. Жесткие ограничения состоят из точных значений меток пикселя,
которые должны быть сохранены по всем кадрам видео.
Эти ограничения используются для определения положения пикселя, которые будут иметь такую же метку
(объект или фон) во всей видеопоследовательности и не внесены в гистограмму цветов.
функции энергии (9)
МСП [3]. Жесткие ограничения состоят из точных значений меток пикселя,
которые должны быть сохранены по всем кадрам видео.
Эти ограничения используются для определения положения пикселя, которые будут иметь такую же метку
(объект или фон) во всей видеопоследовательности и не внесены в гистограмму цветов.
Поставлены жесткие ограничения на сегментацию, включенную в вероятность терма  .
Это сделано путем установки очень высокой стоимости за назначения метки,
которая нарушает жесткие ограничения.
Рис. 4 представляет использование ограничений в процессе сегментации изображения.
Результаты сегментации показаны на Рис. 5.
.
Это сделано путем установки очень высокой стоимости за назначения метки,
которая нарушает жесткие ограничения.
Рис. 4 представляет использование ограничений в процессе сегментации изображения.
Результаты сегментации показаны на Рис. 5.

Рис. 4: Сегментация, использующая ограничения пользователя. Первое изображение - вводное, показывает мягкие ограничения. Ограничения представлены черными (фоном) и белыми (передний план) прямоугольниками. Второе изображение показывает сегментацию, полученную при использовании мягких ограничений, содержит некоторую часть фона, неправильно отмеченного как передний план из-за подобия интенсивности цвета. Третье изображение - результат сегментации, полученный при использовании жесткого ограничения на область вместе с мягким ограничением.

Рис. 5: Результаты Сегментации Прогулки Хромого Человека в Видеопоследовательности.
6.2. Оценка Работы
Проверено тестирование динамического алгоритма сокращения графа в ряде видеопоследовательности и выполнено сравнение его работы с работой алгоритма дерева с двойным поиском, предложенным в [4]. Алгоритм экспериментально показал, что является самым быстрым для некоторых задач компьютерного зрения, включая сегментацию изображения.
Видеопоследовательности, используемые в испытаниях, имели от одной сотни до тысячи кадров изображения. Для всех видео последовательностей динамическое обновление остаточного графа произвело существенное уменьшение числа увеличивающихся путей. Динамические алгоритмы (нормальный и оптимизированный) работают существенно быстрее, чем статический алгоритм.
7. Заключение
В этой статье представлен новый, полностью динамический алгоритм для решения "st-mincut" задачи, который может быть использован для обнаружения МАР решений для быстроизменяющихся динамических МСП. Необходимо отметить, что метод обобщенный и находит точные решения по всем динамическим задачам, которые могут быть оформлены парами МСП. Результаты показывают, что алгоритм работает существенно быстрее, чем всем известный "st-mincut" алгоритм, который повторно вычисляет решение от начала. Продемонстрировано, как этот метод может использоваться, чтобы выполнить сегментацию изображения в реальном масштабе времени в видеопоследовательностях.
Ссылки
[1] R. Ahuja, T. Magnanti, and J. Orlin. Network Flows. Prentice
Hall, Eaglewood Cliffs, NJ, 1993.
[2] A. Blake, C. Rother, M. Brown, P. Perez, and P. Torr. Interac-tive
image segmentation using an adaptive gmМСП model. In
ECCV04, pages Vol I: 428–441, 2004.
[3] Y. Boykov and M. Jolly. Interactive graph cuts for optimal
boundary and region segmentation of objects in n-d images.
In ICCV, pages I: 105–112, 2001.
[4] Y. Boykov and V. Kolmogorov. An experimental comparison
of min-cut/"max-flow" algorithms for energy minimization in
vision. PAMI, 26(9):1124–1137, September 2004.
[5] Y. Boykov, O. Veksler, and R. Zabih. Markov random fields
with efficient approximations. In CVPR, pages 648–655,
1998.
[6] Y. Boykov, O. Veksler, and R. Zabih. Fast approximate en-ergy
minimization via graph cuts. In ICCV, pages I: 377–384,
1999.
[7] Y.-J. Chiang and R. Tamassia. Dynamic algorithms in com-putational
geometry. Technical Report CS-91-24, 1991.
[8] R. F. Cohen and R. Tamassia. Dynamic expression trees and
their applications. In SODA, pages 52–61, 1991.
[9] E. A. Dinic. Algorithm for solution of a problem of maximum
flow in networks with power estimation. Soviet Math. Dokl.,
11:1277–1280, 1970.
[10] L. Ford and D. Fulkerson. Flows in Networks. Princeton
University Press, Princeton, 1962.
[11] D. Greig, B. Porteous, and A. Seheult. Exact maximum a pos-teriori
estimation for binary images. RoyalStat, B: 51(2):271–
279, 1989.
[12] H. Ishikawa. Exact optimization for markov random fields
with convex priors. PAMI, 25(10):1333–1336, October 2003.
[13] P. Kohli and P. H. S. Torr. Dynamic energy minimization for
stereo. In preparation, 2005.
[14] V. Kolmogorov and R. Zabih. What energy functions can be
minimized via graph cuts? In ECCV02, page III: 65 ff., 2002.
[15] M. P. Kumar, P. H. S. Torr, and A. Zisserman. Obj cut. In
CVPR05, pages 18–5, 2005.
[16] M. Thorup. Fully-dynamic min-cut. In STOC, pages 224–
230, 2001.


| Библиотека | Реферат | Ссылки | Отчет о поиске | Индивидуальное задание |