ФРАКТАЛЬНЫЕ СВОЙСТВА МИКРОГЕОМЕТРИИ ОБРАБОТАННЫХ ПОВЕРХНОСТЕЙ

Научный  руководитель: Доцент, к.т.н. Матвиенко Андрей Васильевич

 

Как известно создание поверхностей с определенными микрогеометрическими свойствами является одной из основных задач машиностроения. Особенно это относится к поверхностям особо ответственных изделий авиа-космической техники, приборостроения, прецизионного станкостроения и т.д. Более того, вопрос обеспечения микрогеометрии поверхности особенно актуален при освоении новых технологий обработки поверхностей как механическими, так и физико-химическими способами обработки, в области микро- и нанотехнологий.

Качество поверхности традиционно характеризуются шероховатостью – среднеарифметическим отклонением, максимальной высотой неровностей, средним шагом неровностей профиля и т.п. и физико-механическими свойствами поверхностного слоя [1]. Шероховатость поверхности, как показали многие исследователи, является одним из основных показателей качества поверхности. Во многих случаях именно микрогеометрия поверхностного слоя предопределяет поведение поверхности в процессе ее эксплуатации, а в случае микро- и нанотехнологий шероховатость рассматривается не как вторичная структура, а как свойство самой структуры материала.

Как правило, микрогеометрия поверхностного слоя рассматривается как некий статический объект, который сформировался в процессе некоторого воздействия. Классически в обработке материалов резанием шероховатость является геометрическим прообразом траектории перемещения инструмента, которая задается кинематикой и режимами обработки. С другой стороны в процессе обработки формируются силовые, температурные и др. поля, происходит химическое воздействие на поверхность, возникают высокие давления в зоне контакта инструмента и обрабатываемой поверхности, движение дислокаций и т.д., вследствие чего изменяется структура поверхностного слоя. Поэтому формирование поверхности в целом, и микрогеометрии в частности, является результатом действия совокупности процессов, а не только чисто геометрических «откликов» действия инструмента, как, например, отмечается в работе [2].

В рамках рассматриваемой концепции «коллективного» формирования шероховатости можно сказать, что такой объект, как микрогеометрия поверхности является динамической системой. Изучение динамической системы предполагает изучение ее свойств, которые определяются некоторыми инвариантами (например, показатель Ляпунова, энтропия и т.д.). Поэтому в этом случае использование классических геометрических параметров шероховатости является недостаточным или просто невозможным. Более того, геометрические параметры не отображают такое важное свойство шероховатости как динамической системы – эволюцию.

Таким образом, необходимы новые подходы в оценке микрогеометрии поверхности и одним из таких подходов может быть использование теории фракталов. Применение теории фракталов позволит внести новый показатель для оценки шероховатости, создать базу не только для фрактальной классификации, но прогнозирования изменения микрогеометрии в процессе ее формирования, как на стадии обработки технологическими методами, так и на стадии эксплуатации. Целью данной работы является проверка выдвинутых предположений с позиций теории фракталов на примере формирования микрогеометрии поверхности на этапе технологических воздействий.

Краткие положения теории фракталов

В общем, фрактал – геометрический объект (линия, поверхность, пространственное тело) характеризующийся нерегулярностью (структуры, геометрии и т.п.), но самоподобием (или симметрией) [3,4]. Самоподобие означает, что объект более или менее единообразно устроен на различных масштабах его рассмотрения. Например, на рисунках показано образование фрактальных объектов методом итераций.

 

              

     (  http://www.cs.wisc.edu/~ergreen/honors_thesis/examples.html)

             Т.е. предполагается неизменность основных геометрических особенностей объекта при изменении масштаба. Естественно существуют границы этих масштабов связанные с понятием конечной «массы» объекта. Нерегулярность объекта, в общем, означает некоторую его дробную (фрактальную) размерность, отличающую его от размерности линии, поверхности или пространства. Поэтому в теории фракталов используют понятия топологической размерности и, т.н., размерность Хаусдорфа-Безиковича, которая и характеризует «отклонения» фрактала (объекта) от идеальной топологии. Таким образом, фракталы можно рассматривать как множество точек, вложенных в пространство.

Фрактальная размерность является одной из основных характеристик фрактала. Центральное место в определении фрактальной размерности D (размерность Хаусдорфа-Безиковича) занимает понятие расстояния между точками в пространстве. Следовательно, для определения D необходимо измерить «величину» множества точек в пространстве. Простой способ измерить длину кривых, площадь поверхностей или объем тела состоит в том, чтобы разделить тело на небольшие отрезки, прямоугольники, кубы или сферы. Подсчитывая число этих элементов, необходимых для покрытия интересующего множества точек, получаем меру величины множества.

Фрактальная геометрия основывается на экспериментальном факте, что в общем случае длина L произвольной кривой (которая может быть изломана в любой точке) степенным образом зависит от масштаба измерения δ:

L = C⋅δ^1-D,

где С - размерный множитель, свой для каждой кривой, D - фрактальная размерность.

Другой характеристикой фракталов является корреляционная размерность. Корреляционная размерность D₂ определяется из выражения [26,28]:

,

где p_i² - вероятность того, что наугад взятая точка принадлежит i-й ячейки (кубика).

- минимальное число n-мерных кубиков с ребром e, необходимых для покрытия геометрического объекта.

Корреляционную размерность можно представить в виде [4]:

,

где I(e) – парный корреляционный интеграл, определяемый из выражения:

,

где Q(х) - функция Хевисайда;

r_n, r_m – радиусы-векторы пары точек n и m соответственно.

Парный корреляционный интеграл определяет вероятность того, что две наугад взятые точки разделены расстоянием меньшим, чем e. Кроме того,

 

,

т.е. фрактальная размерность D₂ определяет зависимость парного корреляционного интеграла от e.

Таким образом, размерность D₂ определяется значением корреляционного интеграла, характеризующим относительное число пар точек (n,m), удаленных на расстояния меньшим e.

Следующей характеристикой фрактальных свойств объекта является корреляционная энтропия или информационная размерность, которая в той или иной мере учитывает частоту попадания точки множества в элемент разбиения объекта. Числовое значение энтропии является количественной характеристикой степени хаотичности системы.

Корреляционная энтропия D₁ определяется из следующего выражения [4]:

,

где  - энтропия фрактального множества,

 - вероятность нахождения точки объекта в i-й ячейке разбиения объекта.

Корреляционная энтропия может быть вычислена через корреляционный интеграл.

            Как правило, определение корреляционной размерности и энтропии осуществляется для мультифракталов – неоднородных фрактальных объектов, которые имеют не только геометрические, но и статистические характеристики. Другими словами неоднородные фракталы имеют неравномерное распределение точек множества или разную плотность «заселенности» множества. Поэтому при исследовании мультифракталов говорят об обобщенной фрактальной размерности [3,4], которая может быть представлена вышепредставленными фрактальными размерностями. Но в связи с особой спецификой мультифракталов для анализа используют функцию  мультифрактального спектра или спектр сингулярностей мультифрактала. Как отмечено в работе [4], величина функции мультифрактального спектра фактически равна хаусдорфовой размерности (D) некоторого однородного фрактального подмножества из исходного множества, которое дает доминирующий вклад в статистические характеристики множества. Поэтому в первом приближении можно считать, что D является фрактальной размерностью относительно однородных фракталов в мультифрактальном множестве.

Таким образом, к основным характеристикам фрактала относятся его размерности: обобщенная или хаусдорфова D, корреляционная D₂ и информационная D₁.

Показатель Херста

Существуют различные способы определения фрактальных размерностей, к числу которых относится т.н. R/S-способ, на основании, которого определяется показатель Херста [3]. Этот показатель имеет широкое применение в анализе временных рядов благодаря своей замечательной устойчивости. Он содержит минимальные предположения об изучаемой системе и может классифицировать временные ряды. Он может отличить случайный ряд от неслучайного, даже если случайный ряд не гауссовский (то есть не нормально распределенный).

Для сравнения различных типов временных рядов Херст ввел следующее соотношение:

R/S=(a·N)^Н,

где R/S – нормированный размах от накопленного среднего, N – число наблюдений, а – некоторая константа, Н – показатель Херста.

Имеются три различных классификации для показателя Херста:

1) Н = 0.5. Указывает на случайный ряд. События случайны и некоррелированны. Настоящее не влияет на будущее. Функция плотности вероятности может быть нормальной кривой, однако, это не обязательное условие. R/S-анализ может классифицировать произвольный ряд, безотносительно к тому, какой вид распределения ему соответствует.

2) 0 ≤ Н< 0.5. Данный диапазон соответствует антиперсистентным, или эргодическим, рядам. Такой тип системы часто называют – «возврат к среднему». Если система демонстрирует «рост» в предыдущий период, то, скорее всего, в следующем периоде начнется спад. И наоборот, если шло снижение, то вероятен близкий подъем. Устойчивость такого антиперсистентного поведения зависит от того, насколько Н близко к нулю. Такой ряд более изменчив, чем ряд случайный, так как состоит из частых реверсов спад-подъем.

3) 0.5 < Н < 1.0. Имеем персистентные, или трендоустойчивые ряды. Если ряд возрастает (убывает) в предыдущий период, то, вероятно, что он будет сохранять эту тенденцию какое-то время в будущем. Чем ближе Н к 0.5, тем более зашумлен ряд и тем менее выражен его тренд. Персистентный ряд – это обобщенное броуновское движение, или смещенные случайные блуждания. Сила этого смещения зависит от того, насколько Н больше 0.5.

Существует еще и четвертая характеристика показателя Херста, когда Н>1. В этом случае говорят о статистике Леви и о процессе (или временном ряде) с фрактальным временем, о временных точках разрыва производной. Это означает, что происходят независимые скачки амплитуды, распределенные по Леви за время, определенное величиной скачка, и растущее вместе с ним. Дисперсия приращения за данный интервал времени становится конечной, траектория в фазовом пространстве сохраняет свой вид, но появляется новый фрактальный объект - временные точки разрыва производной.

Если в двойных логарифмических координатах найти наклон R/S как функцию от N, то тем самым получим оценку Н. Эта оценка не связана с какими-либо предположениями относительно лежащего в основе распределения, хотя предпринимаются некоторые попытки классификации случайных распределений на основе фрактальной шкалы [5].

Для очень большого количества наблюдений N можно ожидать сходимости ряда к величине Н=0.5, так как эффект памяти уменьшается до того уровня, когда становится незаметным. Другими словами, в случае длинного ряда наблюдений можно ожидать, что его свойства станут неотличимы от свойств обычного броуновского движения, или простого случайного блуждания, поскольку эффект памяти рассеивается.

Показатель Херста может быть преобразован во фрактальную размерность D с помощью следующей формулы [3-5]:  

                                                    D=2-H

Фрактальная размерность временного ряда, или накопленных изменений при случайном блуждании, равна 1.5. Фрактальная размерность кривой линии равна 1, а фрактальная размерность геометрической плоскости равна 2. Таким образом, фрактальная размерность случайного блуждания лежит между кривой линией и плоскостью. Если Н = 0.5, то D = 1.5. Обе величины характеризуют независимую случайную систему. Величина 0.5 < Н ≤ 1 будет соответствовать фрактальной размерности, более близкой к кривой линии. Это персистентный временной ряд, дающий более гладкую, менее зазубренную линию, нежели случайное блуждание. 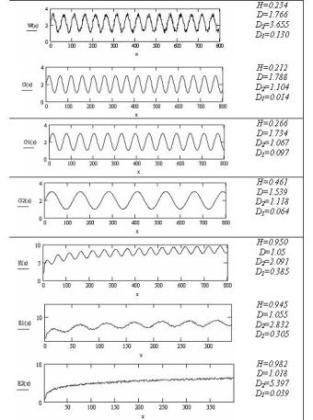Антиперсистентная величина Н (0 < Н < 0.5) дает соответственно более высокую фрактальную размерность и более прерывистую линию, чем случайное блуждание, и, следовательно, характеризует систему, более подверженную переменам.

Для примера на рис.1 представлены графики различных функций с показателем Херста (H), фрактальной размерностью (D), корреляционной размерностью (D₂) и корреляционной энтропией (D₁).

Из приведенных фрактальных характеристик легко можно проследить за их изменением по изменению формы графиков функций. Так, более «зашумленные» функции по своим фрактальным характеристикам отличаются от идеальных. Например, функции W(x) и G(x) описываются одинаковыми выражениями, но в W(x) добавлена шумовая компонента, равномерно распределенная на инт ервале [0-0.5]. Если рассмотреть, например, синусоидальные функции G(x), G1(x) и G2(x) то можно заметить, что с увеличением периода функции показатель Херста приближается к Н=0.5. Это говорит о «приближении» функции к прямой, т.е. синусоида «вытягивается» в прямую.

Рис.1. Фрактальные характеристики функций

Функции Е(х), Е1(х) и Е2(х) типичные представители персистентных рядов. Шум в Е2(х) незначителен по сравнению с общей трендоустойчивостью, поэтому показатель Н больше, чем для функций Е(х) и Е1(х), где явно выражены не только трендоустойчивость, но и периодичность. Причем явно различные периоды не значительно влияют на изменение показателя Н по сравнению с функциями G(x), G1(x) и G2(x). Функция А(х) представляет собой случайное блуждание аргумента, что отображает показатель Н близкий к 0.5.

Таким образом, из приведенных примеров видна взаимосвязь между видом функции (временного ряда) и показателем Херста, что говорит о возможности его использования для классификации функций (рядов). Между тем, существует еще одна особенность определения показателя Херста. Как отмечалось выше для его определения необходимо аппроксимировать прямой R/S как функцию от N в двойных логарифмических координатах. Но при этом, как правило, не выделяются характерные участки функции log[R/S(N)] и аппроксимация осуществляется т.н. «усреднением». Например, для функции W(x) имеем показатель Херста, четко указывающий на периодичность (антиперсистентность), но ничего не говорящий о случайной составляющей, которая не существенна по сравнению с явно выраженной периодичностью. 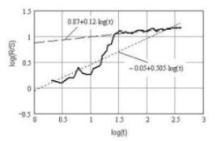Для выявления таких характерных особенностей функций (временного ряда) целесообразно выполнять аппроксимацию не по «среднему» функции log[R/S(N)], а по характерным участкам этой функции. Например, на рис. 2 представлен график функции log[R/S(N)] (на рисунке количество наблюдений или отсчетов N обозначено через t), построенной по функции W(x), где аппроксимации подвержены два характерных участка.

 

Рис.2. График функции log[R/S(t)] для W(x) и его аппроксимации

Как видно из рисунка два характерных участка хорошо аппроксимируются соответствующими прямыми, которые указывают на показатели Херста 0.12 и 0.505, что соответствует периодичности и зашумленности функции W(x).

 

Фрактальная характеристика микрогеометрии поверхностного слоя

Для изучения фрактальных характеристик микрогеометрии поверхностного слоя были использованы профилограммы, полученные после различных видов механического воздействия на обрабатываемую поверхность стальных заготовок. Фрактальная размерность профилограмм оценивалась по приведенным выше характеристикам: показатель Херста, корреляционная размерность и корреляционная энтропия. Показатель Херста определялся как по «усреднению» всех аргументов (длины профилограммы), так и по характерным участкам функции log[R/S(t)].

Более детальным исследованиям подвергались профилограммы, полученные после обработки точением на различных режимах подачи и скорости резания.

На рис.3 представлены графики зависимостей показателя Херста микропрофиля поверхности, рассчитанного по «усреднению» функции log[R/S(t)], от подачи и скорости резания. Как видно из рисунка, показатель Н находится в диапазоне 0.5...1, что указывает на персистентность профилограмм. На некоторых режимах обработки отмечается случайное блуждание микропрофиля поверхности, т.е. Н®0.5. Характер изменения показателя Н указывает на то, что микропрофиль поверхности, полученный точением носит нерегулярный характер, т.е. есть тенденция к его увеличению по ходу обработки. Это гипотетически соответствует, например, функциям Е(х), Е1(х) и Е2(х) (рис.1) и может косвенно указывать на проявление таких технологических факторов, как износ инструмента, вибрации, недостаточная жесткость системы и др.

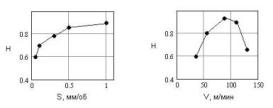
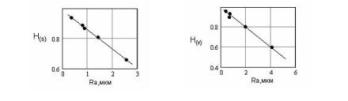
Рис.3 Типичные зависимости показателя Херста микропрофиля поверхности от подачи и скорости резания при точении.

На рис.4 представлены типичные зависимости показателя Херста микропрофиля поверхности от среднеарифметического значения высоты неровностей.

Рис.4 Типичные зависимости показателя Херста микропрофиля поверхности от среднеарифметического значения высоты неровностей (H_(s) – показатель Херста от влияния подачи , H_(v) – показатель Херста от влияния скорости резания)

Но, как указывалось выше, функции log[R/S(t)], по которым определяется показатель Херста, имеют характерные участки, указывающие как на периодичность, так и на случайность микропрофиля поверхности (рис.5).

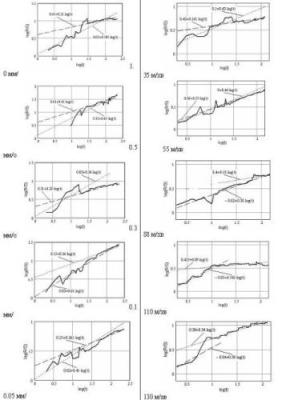
Рис. 5 Графики функций log[R/S(t)] для профилограмм, полученных на различных режимах обработки при точении стали 45

На рис. 5 представлены графики log[R/S(t)], построенные для профилограмм поверхностей, обработанных на различных режимах при точении. Как видно из рисунка все функции имеют два характерных участка, отображающих, как «шумовую», так и периодическую составляющие микропрофиля поверхности. Угловой коэффициент аппроксимирующих прямых указывает на показатель Херста. Анализируя графики рис.5 можно отметить, что при увеличении подачи превалирует периодическая составляющая микропрофиля поверхности, а при увеличении скорости резания – шумовая. В то же время обращает на себя внимание вид графиков на рис.4, указывающие на некоторые особенности формирования шероховатости при точении. В этом случае представляет интерес исследование «масштабируемости» микропрофиля поверхности, который может быть оценен через зависимость высоты профиля (Ra) от количества «выступов-впадин» (N_L) на фиксируемой длине профилограммы. На основании экспериментальных исследований получены графики таких зависимостей в двойных логарифмических координатах (рис.6), аппроксимированные прямыми. Полученные зависимости являются типичным фрактальными, т.е. проявляется масштабная инвариантность микропрофиля - с увеличением высоты неровностей уменьшается количество «выступов-впадин».

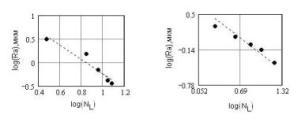
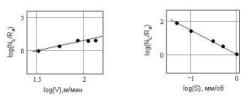
Рис. 6 Зависимость среднеарифметического значения высоты неровностей (R_a) от количества «выступов-впадин» (N_L) на фиксируемой длине профилограммы при изменении скорости резания (а) и величины подачи (б) при точении стали 45. Соответствующие фрактальные размерности »1.62 и »1.92.

На рис. 7 показаны зависимости log(N_L/R_a) от логарифма величин скорости резания (а) и подачи (б). 

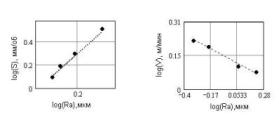
Рис. 7 Зависимости   log(N_L/R_a)  от логарифма величины скорости резания (а) и подачи (б). Соответствующие фрактальные размерности »1.74 и »1.38.

На рис. 8 представлены зависимости log(S) и log(V) от логарифма среднеарифметического значения высоты неровностей. Как показывают рисунки 7 и 8 значения данных в логарифмических масштабах располагаются практически на одной прямой, что говорит об их фрактальной природе.

 

Рис. 8. Зависимости log(S) и log(V) от log(Ra) при токарной обработке стали 45. Соответствующие фрактальные размерности »1.89 и »1.28.

Таким образом, проявление фрактальных свойств микрорельефа поверхности говорит о его самоподобии. Причем самоподобие проявляется не только относительно геометрического масштабирования, но и относительно режимов обработки. Очевидно, наблюдаемое самоподобие достигается путем повторения механизма предыдущего технологического воздействия на поверхность, но в другом «масштабе». В таком случае необходимо выяснить этот механизм «повторяемости», что, скорее всего, возможно только с позиций синергетики и фрактального материаловедения [6,7]. Кроме того, можно предположить, что фрактальные свойства поверхностного слоя отображают процессы его самоорганизации с точки зрения иерархичности фрактальных структур. Выявление такого рода иерархий позволит прогнозировать и управлять качеством поверхностного слоя деталей машин.

Выводы

На основании выполненных исследований установлено:

1)      фрактальная размерность микропрофиля обработанных поверхностей может являться одной из важных его характеристик, которая зависит от условий обработки;

2)      R/S-анализ профилограмм поверхностей и определение на его основе показателя Херста позволяет оценить характер микрорельефа с точки зрения периодичности (регулярности) и «зашумленности», а также определить фрактальную размерность;

3)      микрорельеф поверхности (среднеарифметическое значение, Ra) является самоподобным или масштабно-инвариантным относительно режимов обработки (показано на примере точения);

4)      функциональная зависимость между параметром шероховатости Ra и режимами обработки может быть определена через фрактальную размерность.

Литература. 1. Качество машин: Справочник. В 2 т. Т.1 / А.Г. Суслов, Э.Д. Браун, Н.А. Виткевич и др. – М.: Машиностроение, 1995. – 256 с.

 2. А.А. Потапов, В.В. Булавкин, В.А. Герман и др. Исследование микрорельефа обработанных поверхностей с помощью методов фрактальных сигнатур. // Журнал технической физики, 2005, том 75, вып. 5. – С. 28-45.

3. Федер Е. Фракталы. Пер. с англ. – М.: Мир, 1991. – 254 с.

4. Божокин С.В., Паршин Д.А. Фракталы и мультифракталы. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. – 128 с.

5. Ю.Н. Кликушин. Фрактальная шкала для измерения формы распределений вероятности // Журнал радиоэлектроники № 3, 2000. – С. 15-18.

 6. Хакен Г. Синергетика. - М.: Мир, 1980. – 400с.

7. Иванова В.С., Баланкин А.С., Бунин И.Ж. и др. Синергетика и фракталы в материаловедении. - М.: Наука, 1994. – 383 с.