 ДонНТУ Портал магистров ДонНТУ
ДонНТУ Портал магистров ДонНТУ ДонНТУ Портал магистров ДонНТУ
ДонНТУ Портал магистров ДонНТУ

|
Автореферат по теме: "Оценка влияния колебаний напряжения на человека при наличии в сети электроприемников с резкопеременной нагрузкой" |
СОДЕРЖАНИЕ
1.1 Динамические модели электромагнитной совместимости
1.3 Методы расчета характеристик реакций
1.4 Постановка задач исследований
2.Расчет дозы фликера напряжения от дуговых сталеплавильных печей
2.1 Разложение взвешивающего фильтра фликер-модели по методу парциальных реакций
2.2 Дуговые сталеплавильные печи как источник электромагнитных помех
Введение
Рост единичной мощности и количества электроприемников с резкопеременной нагрузкой (дуговые печи, рудно-термические установки, прокатные станы, бытовые приборы) сделали задачу оценки допустимости создаваемых ими колебаний напряжения весьма актуальной. Об этом свидетельствует нормирование колебаний напряжения в [1] и стандартах Международной электротехнической комиссии (МЭК).
Колебания напряжения вызывают колебания действующих значений светового потока ламп, а, следовательно, и освещенности. Это приводит к дополнительному утомлению людей и, как следствие, к снижению производительности труда и ухудшению здоровья. Допустимость колебаний напряжения оценивается по дозе фликера напряжения, которая нормируется стандартами МЭК и ГОСТ 13109-97.
В проектировании систем электроснабжения возникает необходимость в прогнозировании доз фликера напряжения по известным характеристикам электрической нагрузки источников помех – электроприемников с резкопеременной нагрузкой.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1 Динамические модели электромагнитной совместимости
Оценка ЭМС заключается в оценке реакции Y(t) объекта на помеху X(t). В связи с этим требуются математические описания помехи и объекта, которые обычно называют моделями.
Чаще всего применяются динамические модели. Принцип динамического моделирования ЭМС был сформулирован в работе [1]. Типичная структура динамической модели ЭМС представлена на рисунке 1.2. Входной блок 1 выделяет из входного процесса U(t) помеху X(t). Линейный фильтр 2 моделирует реакцию Y(t) объекта на помеху. Блок 3 квадратичного сглаживания содержит квадратор и инерционное (апериодическое) или кумулятивное звено (окно Дирихле). Тем самым учитывается, что воздействие помех определяется энергией реакции и не может проявиться мгновенно. В блоке 4 статистической обработки вычисляется расчетное значение динамического показателя ЭМС: для большинства показателей – непосредственно по процессу S(t) после блока 3 или со взвешивающими коэффициентами – для дозы фликера (п. 1.5).

Рисунок 1.1 – Структура динамической модели ЭМС
При нулевых начальных условиях фильтр описывается передаточной функцией W(p), которая определяет амплитудно-частотную А(ω), переходную h(t) и весовую h(t)=h'(t) функции, где р – оператор дифференцирования, ω – угловая частота. Порядок n многочлена в знаменателе передаточной функции определяется порядком линейного дифференциального уравнения с постоянными коэффициентами, которое описывает связь между входными и выходными процессами в фильтре.
Часто в фильтрах динамических моделей используются колебательные звенья, например в фильтре фликерметра Международной электротехнической комиссии – прибора, с помощью которого оценивается допустимость колебаний напряжения в электрических сетях.
Колебания напряжения занимают особое положение среди потребительских свойств электроэнергии, так как они затрагивают здоровье человека: быстрые изменения освещенности, вызванные колебаниями напряжения на зажимах ламп, дополнительно утомляют человека, что ведет к ухудшению зрения и уменьшению производительности труда. В связи с этим задача объективной оценки допустимости колебаний является весьма актуальной.
В документах Международной электротехнической комиссии (МЭК) [3, 4] описана модель фликерметра – прибора, оценивающего допустимость колебаний напряжения в электрических сетях. Данная модель принята и в стандарте Украины на качество электроэнергии [2]. В работе далее используется термин "фликер-модель".
Основу фликер-модели составляет взвешивающий фильтр (рисунок 1.2), который включает в себя: 1 – высокочастотный (ВЧ) фильтр первого порядка с частотой среза fc1=0,05 Гц , 2 – фильтр Баттерворта 6-го порядка с частотой среза fc2=35 Гц и 3 – фильтр восприятия.
Рисунок 1.2 – Структурная схема взвешивающего фильтра фликер-модели
Передаточная функция ВЧ фильтра первого порядка, который состоит из инерционного и дифференцирующего звеньев [5, стр. 30].
Фильтр Баттерворта 6-го порядка состоит из трех последовательно соединенных колебательных звеньев [6, стр. 90].
Фильтр восприятия состоит из последовательно соединенных колебательного, двух инерционных, дифференцирующего и форсирующего звеньев.
Общая передаточная функция взвешивающего фильтра фликер-модели представляет собой произведение передаточных функций трех фильтров: ВЧ, Баттерворта и восприятия: WФВ(p)=W1(p)W2(p)W3(p) (1.1)
Таким образом, процессы во взвешивающем фильтре описываются дифференциальным уравнением одиннадцатого порядка. Расчет характеристик реакции зрения сводится к решению этого дифференциального уравнения.
1.2 Доза фликера напряжения
Задачей работы является применение новых методов для расчета реакций фильтров динамических моделей ЭМС на случайные электромагнитные помехи: применительно к фликерметру – реакции взвешивающего фильтра, и далее – для расчета динамических показателей ЭМС, а именно – дозы ликера напряжения.
Нормирование кривых колебаний обладает существенными недостатками.
Понятие дозы фликера основано на оценке дискомфорта человека от колебаний силы света [7]. Фликер-модель для оценки дозы фликера напряжения [3, 4] состоит из трех блоков: взвешивающего фильтра ФВ, квадратичного инерционного сглаживания КС и статистической обработки ОС (рисунок 1.3). Под помехой X(t) понимается разность между процессом U(t) и его одноминутным трендом. Помеха измеряется в процентах от уровня номинального напряжения Uн.
Взвешивающий фильтр моделирует лампу накаливания (60 Вт, 230 В) и зрительную систему человека.
Частота колебаний FδUt в [2] измеряется в мин–1, что соответствует частоте изменения процесса λ=FδUt/120 в Гц или угловой частоте ω=2πλ в с–1.
Рисунок 1.3 – Структурная схема фликер-модели (рисунок анимирован:18 кВ;5 циклов)
Процесс Y(t) на выходе ФВ называется реакцией зрения, которая измеряется в процентах. Блок КС моделирует ощущение фликера S(t). Блок состоит из квадратора 4 и апериодического инерционного звена 5 первого порядка, которое сглаживает процесс Z(t)=Y2(t) с постоянной времени Tи=0,3 c и коэффициентом передачи kи=100(%)-2 , который делает величину S безразмерной [8]. В последнем блоке на графике S(t) проводятся различные уровни фликера Pr и строится функция Er(Pr) кумулятивных вероятностей Er, выражаемых в процентах. Вероятность связана с функцией распределения F(S) ощущений фликера соотношением
Er(Pr)=100[1-F(S)]|S=Pr
По значениям Er = 0,1; 1; 3; 10 и 50 % находятся соответствующие уровни фликера Pr=arc Er(Pr). Кратковременная доза фликера определяется по формуле
Допустимое значение кратковременной дозы равно единице.
В [2] также нормируется длительная доза фликера PLt , определяемая как средняя величина 12 значений кратковременных доз за 2 часа ([2], формула Б.11). Ее допустимое значение равно 0,74. В стационарном режиме дозы совпадают.
В табл. 1.1 приведены допустимые значения доз фликера напряжения из ГОСТ 13109-97.
Таблица 1.1 – Допустимые значения доз ликера напряжения
1.3 Методы расчета характеристик реакций
Анализ существующих моделей ЭМС подтверждает, что основной задачей оценки динамических показателей ЭМС является определение характеристик реакции Y(t) на выходе линейного фильтра: среднего значения Yс(t) и корреляционной функции KY(t1, t2) или только дисперсии DY(t).
Эта задача может быть решена применением общих формул теории случайных процессов [11, 12, 13 – 17, 18, 19].
Вычисление среднего значения не встречает затруднений. Только при большом порядке n дифференциального уравнения будут необходимы громоздкие выкладки для нахождения переходных функций h(t). Иначе обстоит дело с КФ. Поскольку в КФ помехи присутствует модуль аргумента τ, поэтому при определении КФ и дисперсий реакции необходимо дважды выполнять громоздкое двойное интегрирование: при τ + u<ν и τ + u>ν. Точно так же вычисление КФ и дисперсии с помощью теоремы о вычетах является достаточно трудоемким. Кроме того, каждый раз при проектировании пользователю необходимо заново вычислять характеристики реакции для разных видов КФ помехи и передаточных функций. Все это требует специальной подготовки пользователя.
Указанные недостатки методов расчета реакций фильтров устраняются путем применения метода парциальных реакций, предложенного на кафедре ЭПГ ДонНТУ [9].
1.4 Постановка задач исследований
Из анализа литературы следует, что предлагаемые в действующем ГОСТ 13109-97 методы расчета показателей ЭМС, а в частности дозы фликера напряжения, обладают существенными недостатками. В связи с этим в работе поставлены следующие задачи исследований:
1. Предложенный в [9] метод расчета характеристик случайных процессов на выходе линейных фильтров моделей ЭМС применить для расчета доз фликера напряжения, создаваемым разными группами электроприемников.
2. Провести анализ выполненных расчетов с точки зрения влияния точности определения дозы фликера напряжения на качество электроэнергии.
2 РАСЧЕТ ДОЗЫ ФЛИКЕРА НАПРЯЖЕНИЯ ОТ ДУГОВЫХ СТАЛЕПЛАВИЛЬНЫХ ПЕЧЕЙ
2.1 Разложение взвешивающего фильтра фликер-модели по методу парциальных реакций
В данной работе предложенный в [9] метод парциальных реакций применяется для определения реакции зрения человека на выходе взвешивающего фильтра фликерметра.
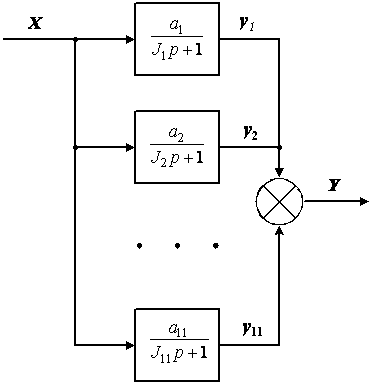
Структурная схема фликер-модели приведена на рис. 1.3 (п.1.2). Передаточная функция взвешивающего фильтра ФВ модели имеет вид (1.1). Порядок знаменателя передаточной функции n=11 , т.е. процессы в фильтре описываются дифференциальным уравнением 11-го порядка. Применяя метод парциальных реакций к фликер-модели, представим ее взвешивающий фильтр в виде 11 параллельно включенных инерционных звеньев (рис. 2.1).
Корни знаменателя передаточной функции:
Рисунок 2.1 - Эквивалентная схема взвешивающего фильтра фликер-модели
Коэффициенты передачи инерционных звеньев
Постоянные времени инерционных звеньев:
и обратные им величины
Подставляя числовые значения постоянных времени фильтра в приведенные формулы, получим:
p1= - 0,314 c-1, p2,3= - 56,913 ± j212,419 c-1, p4,5= - 155,499 ± j155,502 c-1,
p6,7= - 212,423 ± j56,897 c-1, p8,9= - 25,524 ± j51,566 c-1,
p10= - 7,692 c-1, p11= - 137,608 c-1
J 1 = 3,183 c, J2,3= (1,177 ± j4,392)·10-3 c, J4,5= (3,215 ± j3,215)·10-3 c,
J6,7= (4,392 ± j1,177)·10-3 c, J8,9= (7,710 ± j16)·10-3 c,
J10= 0,13 1 c, J11= 7,267·10-3 c.
γ1= 0,314 c-1,
Переходная и весовая функции взвешивающего фильтра фликер-модели определяются согласно следующим выражениям:
2.2 Дуговые сталеплавильные печи как источник электромагнитных помех
Нагрузка I(t) ДСП представляет собой случайный нестационарный процесс. Поэтому в выражение K(t, τ) для КФ помимо аргумента τ входит время t как параметр.
Например, параметры корреляционной функции (КФ) тока печи ДСП емкостью 5 тон являются функциями времени [10]:
DIp(t) - дисперсия тока в кА2;
Iк - эксплуатационный ток КЗ,кА;
tк - длительность периода расплавления, мин.
По методу парциальных реакций в работе определены КФ на выходе ВФ для колебаний напряжения, создаваемых ДСП, и доза фликера напряжения.
На рис. 2.2 представлены графики изменения КФ для разных моментов времени.
Рисунок 2.2 - КФ реакции на выходе взвешивающего фильтра фликерметра от ДСП-5
ВЫВОДЫ
1. Дозу фликера напряжения от ДСП целесообразно расчитывать с помощью метода парциальных реакций и метода иммитации случайных помех.
2. Колебания напряжения, которые создаются ДСП, как правило, превышают допустимый уровень, который нормируется действующим стандартом на качество электрической энергии. Для уменьшения их влияния необходимо принимать дополнительные меры, например, увеличивать мощность трансформатора ГПП.
Список источников:
1. Куренный Э.Г., Ковальчук В.М., Коломытцев А.Д. Оценка качества электроэнергии с использованием моделей объектов // Материалы конференции "Качество электроэнергии в сетях промышленных предприятий". – М.: МДНТП, 1977. – С. 23-29.
2. ГОСТ 13109-97. Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. – Введ. в Украине 01.01.2000.
3. Flickermeter. Functional and design specification. – Geneva: IEC Report. – 1986. – Publication 868. – 31 p.
4. IEC 61000-4-15: Electromagnetic compatibility – Part 4: Testing and measurement techniques. Section 15: Flickermeter – Functional and design specifications, 1997.
5. Лэм Г. Аналоговые и цифровые фильтры: Расчет и реализация. – М.: Мир, 1982. – 592 с.
6. Гутников В.С. Фильтрация измерительных сигналов. – Л.: Энергоатомиздат, 1990. – 192 с.
7. Mirra C., Sani G. Il fenomeno del flicker. Analisi delle sue caracteristiche. Techniche di misura e metodi di limitazione. – L’Elettrotecnica. – 1987. – Р. 805 – 822.
10. Алексеев С.В., Трейвас В.Г. Статистические характеристики токов дуг дуговых сталеплавильных печей // Изв. вузов. Электромеханика. – 1971. – № 1. – С. 78-82.
11. Электромагнитная совместимость электроприемников промышленных предприятий // А.К. Шидловский, Б.П. Борисов, Г.Я. Вагин и др. – К.: Наукова думка, 1992. – 236 с.
12. Шидловский А.К., Куренный Э.Г. Введение в статистическую динамику систем электроснабжения. – К.: Наукова думка, 1984. – 273 с.
13. Свешников А.А. Прикладные методы теории случайных функций. – М.: Наука, 1968. – 464 с.
14. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1969. – 576 с.
15. Тихонов В.И. Статистическая радиотехника. – М.: Советское радио, 1966. – 678 с.
16. Тихонов В.И. Выбросы случайных процессов. – М.: Наука, 1970. – 392 с.
17. Пугачев В.С. Теория вероятностей и математическая статистика. – М.: Наука, 1979. – 496 с.
18. Грибанов Ю.И., Мальков В.И. Спектральный анализ случайных процессов. – М.: Энергия, 1974. – 240 с.
19. Пугачев В.С. Теория случайных функций и ее применение к задачам теории автоматического управления. – М.: Наука, 1962. – 821 с.

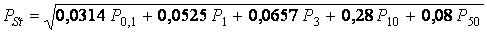 (1.2)
(1.2)
Наименование потребителя
Доза фликера
Электрическая сеть, к которой присоединяют осветительные установки:
кратковременная
длительная
с лампами накаливания в помещениях, где требуется значительное зрительное напряжение
1,0
0,74
с лампами накаливания в остальных помещениях
1,38
1,0
 ,
, 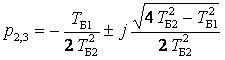 ,
, 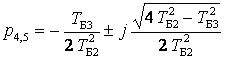 ,
, 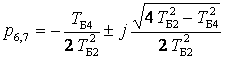 ,
,  ,
,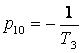 ,
, 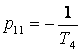 .
.
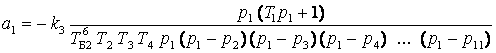 ,
,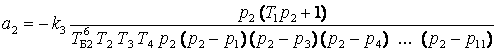 ,
,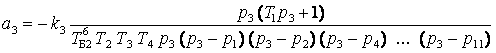 ,
, ,
,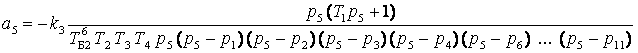 ,
, ,
,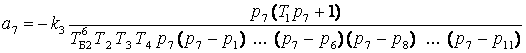 ,
, ,
, ,
, ,
, .
. ,
, ,
,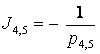 ,
, ,
,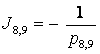 ,
,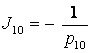 ,
,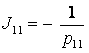 .
.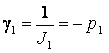 ,
,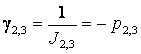 ,
, ,
, ,
,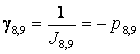 ,
,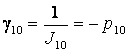 ,
,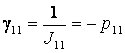 .
.
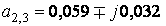 ,
,  ,
, 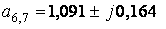 ,
,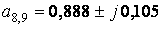 , a10 = - 0,152, a11 = - 4,7 .
, a10 = - 0,152, a11 = - 4,7 .
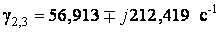 ,
,  ,
, ,
, 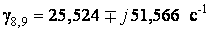 , γ10= 7,692 c-1, γ11= 137,608 c-1.
, γ10= 7,692 c-1, γ11= 137,608 c-1. ,
,  (2.1)
(2.1)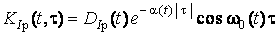 ; (2.2)
; (2.2) ; (2.3)
; (2.3)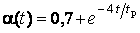 ;
;  , (2.4)
, (2.4)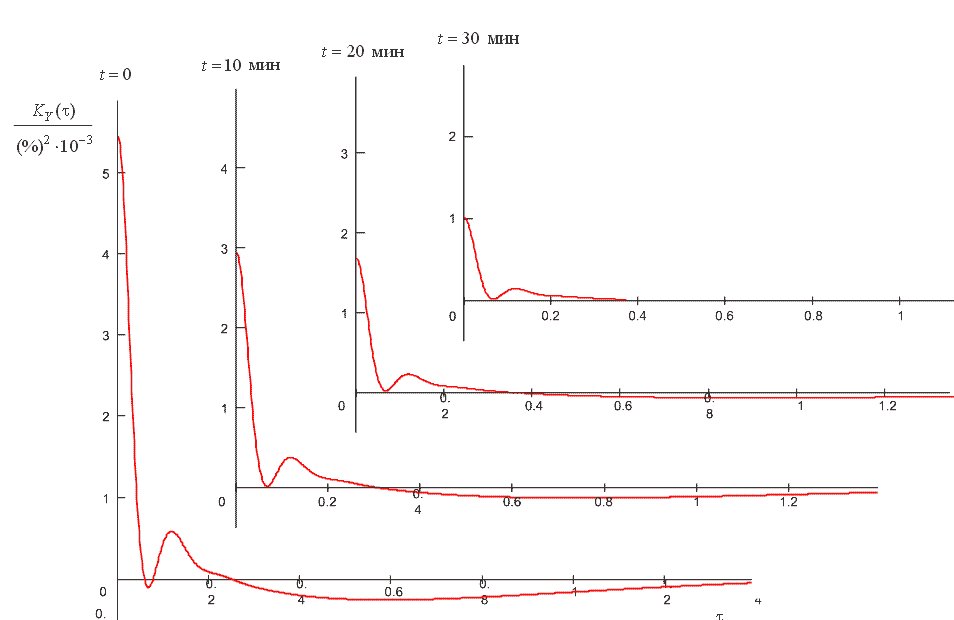
К содержанию
Отчет о поиске
Библиотека
Ссылки
Автобиография
Индивидуальное задание