|
Название Характеристики систем с распределенными параметрами
Источник Статья с конференции
Автор Войтенко А.В.
Год опубликования 2008 год
В развитии естественных наук и техники все большее значение приобретают методы теории сплошных сред и теории полей различной природы. С понятием «поле» или «сплошная среда» мы встречаемся в различных отраслях науки и техники. Основным математическим аппаратом исследования процессов в этих областях служат дифференциальные и интегральные уравнения математической физики.
Развитие общей теории систем и, в частности, систем с распределенными параметрами привело к созданию структурной теории такого рода систем. В основе этой теории лежит теория распределенного блока, который соответствует определенному физическому процессу в сплошной среде и который в линейном случае однозначно и полностью описывается соответствующей функцией Грина или передаточной функцией.
Целью данного доклада является рассмотрение характеристик систем с распределенными параметрами. В нем будут рассмотрены такие вопросы: определение (математическое описание системы с распределенными параметрами), свойства δ-функции, оператор Лапласа в различных системах координат и принцип разбиения задач на группы.
Определение
Все приведенные ниже задачи с граничными (краевыми) и начальными условиями записываются в единой стандартной форме (определение стандартной формы будет приведено ниже). Рассматриваются только линейные задачи.
Неизвестная (вообще говоря, векторная) функция задачи обозначается Q(t,x). Она зависит от пространства переменной (точки) x, принимающей свои значения в открытой области D в r-мерном евклидовом пространстве Er, включая границу ∂D, и от временной переменной (времени) t, принимающей свои значения на числовой полуоси t≥t0.
Будем рассматривать задачи для дифференциальных уравнений с граничными или начальными условиями (в том числе одновременно с теми и другими), описывающих некоторые процессы в определенной пространственной области D с границей ∂D и во времени t≥t0. Кроме дифференциальных уравнений такому же рассмотрению подвергаются и интегральные, и интегро-дифференциальные уравнения.
Пусть основное уравнение задачи записывается в виде
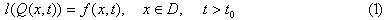
Граничные (краевые) условия записываются в виде

Начальные условия записываются в виде
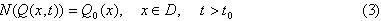
Здесь l,Г,N – некоторые линейные операторы, причем Г – оператор граничных (краевых) условий, N – оператор начальных условий. Задача состоит в определении функций Q(x,t), удовлетворяющей условиям (1), (2), (3). Функции f(x,t), g(x,t), Q0(x) считаются заданніми.
На основании сделанных предположений получены выражения для задач не зависящих от x, для задач не зависящих от t и для общего случая.
Свойства δ-функции
Полученные выражения в первом пункте используют δ-функцию. Для работы с этой функцией рассматриваются различные ее свойства, с которыми чаще всего приходится встречаться при решении задач уравнений математической физики. В презентации рассмотрены основные свойства δ-функции в одномерном (скалярном) случае и многомерном случае.
Оператор Лапласа в различных системах координат
Так же в презентации рассмотрен оператор Лапласа, точнее его применение в различных системах координат. Для рассмотрения выбраны такие системы координат:
- Декартова прямоугольная r-мерная система координат.
- Полярная плоская система координат.
- Цилиндрическая система координат.
- Сферическая система координат.
- Произвольная ортогональная криволинейная r-мерная системы координат.
Принцип разбиения задач на группы
Для облегчения поиска нужной задачи все задачи разбиты на отдельные непересекающиеся группы. Каждая группа кодируется тройкой целых чисел (r.m.n), где
- r – размерность пространственной области D определения функции Q данной задачи.
- m – наивысший порядок производных функции Q по независимой временной переменной t в основном уравнении задачи.
- n – наивысший порядок производных функции Q по пространственным переменным в основном уравнении задачи.
Среди прочих можно выделить такие основные группы: (0.1.0), (0.2.0), (0.m.0), (1.0.1), (1.0.2), (1.0.4), (1.0.n), (1.1.1), (1.1.2), (1.2.2), (1.2.4), (2.0.2), (2.0.4), (2.1.2), (2.2.2), (2.2.4), (3.0.2), (3.1.2), (3.2.2), (r.0.2), (r.1.2).
|