|
Название Уровни распараллеливания сетевых динамических объектов с распределенными параметрами
Источник Статья с конференции
Авторы Войтенко А.В., Чихиро Д.М., Якушик Л.Ю.
Год опубликования 2008 год
Введение
Моделирование сложных динамических систем приобретает всё большую актуальность в отраслях техники, технологий, биотехнологий. Для реализации моделей сложных динамических систем применяются многопроцессорные системы, причём нужно заметить, что вся потенциальная вычислительная мощность такой системы используется не полностью. Для достижения большей продуктивности системы разработчики параллельного программного обеспечения решают проблему распараллеливания программ.
При параллельном моделировании сетевых динамических объектов с распределёнными параметрами (СДОРП) решаются системы с большим количеством уравнений. При этом возникает проблема распределения вычислительной нагрузки по процессам.
Целью данной работы является исследование различных подходов к распределению программной модели сетевых динамических объектов с распределёнными параметрами (СДОРП).
Формальное описание СДОРП
Структура формального описания СДОРП приведена на рисунке 1.

Рисунок 1. Формальное описание СДОРП.
Формальное описание топологии объекта с распределёнными параметрами задаётся с помощью ориентированного графа G(U, V), с множеством узлов |U| = n и ветвей |V| = m. Граф кодируется следующей таблицей:
Таблица 1. Таблица кодирования графа СДОРП.
| NUi |
KUi |
Qi |
Param(P1, P2,… Pt) |
Активный элемент |
| | | |
NUi, КUi - это номера начального и конечного узлов графа соответственно. Qi – идентификатор ветви графа, Param – физические параметры ветвей графа (длина ветви, удельное аэродинамическое сопротивление, площадь поперечного сечения и др.).
Выведем уравнения для формального описания СДОРП:
-
Выделяется бесконечно малый элемент

P – давление воздуха в узле
Q - расход воздуха.
-
Применительно к бесконечно малому элементу рассматривается физический закон динамических процессов.

где a – скорость звука в воздухе;
ρ – плотность воздуха, кг/м3;
F – площадь поперечного сечения воздуховода;
x – координата, отсчитываемая по оси воздуховода.
Данная система описывает изменение расходов воздуха Qj и давлений Pj в функции времени и пространственной координаты.
-
Формуются граничные условия.
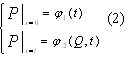
Аппроксимируя уравнения (1) по методу прямых, получим следующую систему для k-го элемента Qj ветви длиной Δx:
ρ – плотность воздуха, кг/м3;
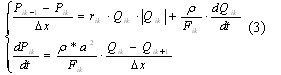
где i - номер ветви, k – номер элемента ветви ( k = 1..Мi ).

li – длина i-ой ветви , Δx - единый для всей сети шаг по пространственной координате.
Граничные условия для уравнений воздушных потоков в ветвях следует разделять на внешние и внутренние. К внешним относятся давления в начальных узлах, чьи ветви соединены с атмосферой, и давление в узлах, к которым подключены вентиляторы. Внутренние граничные условия – это давления в узлах сети, которые описываются уравнениями в виде:
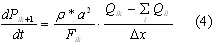
Здесь ΣQil - алгебраическая сумма расходов в элементах ветвей, инцидентных граничному узлу,

И должны быть вычислены при решении сетевой системы уравнений.
На основе уравнений (3) и (4) должна генерироваться система уравнений для всей сети.
Уровни распараллеливания
Для сложного динамического объекта с распределенными параметрами предлагаются следующие уровни распараллеливания:
Первый уровень – уровень процессов минимальной зернистости виртуальной параллельной модели (Virtual parallel Simulation Model). Для данного уровня характерно следующее соотношение: одно уравнение – один процесс. Таким образом можно выделить Р-процессы и Q-процессы. Второй уровень: каждому k-му элементу дискретизированной ветви ставиться в соответствие один процесс. Для данного уровня характерно следующее соотношение: один процесс – два уравнения (вводятся PQ процессы). Третий уровень – «одна ветвь – один процесс». Четвертый уровень – декомпозиция графа СДО на подграфы. Необходимо граф задач T (P, M), где вершины представляют вычисления, а рёбра – обмен данными между вершинами, спроецировать на граф C(PE, K), отображающий целевую ЭВМ.
Априорный анализ уровней распараллеливания
При априорном анализе следует выделить критерии:
Загрузка процессов (при этом под загрузкой понимают работу программы, которую реализует данный процесс). Для оптимального решения задачи моделирования важной является равномерность загрузки процессов. Объем операций обмена. Организация виртуального коммутатора. Коммутатор должен обеспечивать минимальное время обмена информацией между процессами.
Методика построения параллельных симуляторов
При разработке параллельного симулятора важную роль играет целевая параллельная вычислительная система (ЦПВС). Так если ЦПВС является параллельной с объединенной памятью, то для реализации можно использовать стандарт OpenMP, который был специально разработан для систем с общей памятью. Часть средств данного стандарта реализуется непосредственно компилятором, другая – в виде библиотечных функций. Компилятор данного языка способен автоматически распределять потоки между доступными процессорами, так что даже при первом уровне распараллеливания большое количество уравнений не является проблемой. С другой стороны, при использовании OpenMP-стандарта более сложным является обмен данными между потоками и контроль доступа к памяти.
Если же ЦПВС – система с распределенной памятью, то следует использовать библиотеку MPI. При этом не возникает проблем с доступом к памяти, так как каждый процессор имеет свою локальную память и ситуация одновременного чтения исключается. Но наличие распределенной памяти увеличивает время передачи данных между процессорами, что в свою очередь сказывается на быстродействии системы.
Литература
- Абрамов Ф.А., Фельдман Л.П., Святный В.А. Моделирование динамических процессов рудничной аэрологии.К.:Наук.думка, 1981.–284с.
- Святный В.А. «Паралельне моделювання 2006»
|