|
Название Virtuelle Simulationsmodelle und ein Devirtualisierungsvorgang für die Entwicklung der parallelen Simulatoren von komplexen dynamischen Systemen
Авторы V. Svjatnyj, O. Moldovanova, O. Smagin, M. Resch, R. Keller, R. Rabenseifner
Abstract
V. Svjatnyj, O. Moldovanova, O. Smagin Virtual Simulation Models and Devirtualisation Process for the Development of Parallel Simulators of Complex Dynamic Systems. This article deals with approaches for virtual parallel LPDS and DPDS simulation models and approaches for development of parallel simulators. The devirtualisation process is defined and is described with examples.
EinfÜhrung
Eine Implementierung von mathematischen Modellen für komplexe dynamische Systeme mit konzentrierten (DSKP) und mit verteilten (DSVP) Parametern auf modernen parallelen Rechnerarchitekturen gehört zu den aktuellen Forschungsproblemen der parallelen Simulationstechnik. Die Entwicklung von parallelen DSKP- und DSVP-Simulatoren für verschiedene Anwendungsfelder stehen im Mittelpunkt einer engen Kooperation zwischen der DonNTU und dem HLRS auf dem Gebiet von verteilten parallelen Simulationsumgebungen [1].
In dem Beitrag werden Ansätze für virtuelle parallele DSKP- und DSVP-Simulationsmodelle und zur Entwicklung von parallelen Simulatoren betrachtet. Insbesondere wird Devirtualisierungsvorgang definiert und anhand von Beispielen erläutert.
Die DSKP-, DSVP-Simulationsmodelle
Die formale DSKP- und DSVP-Modellierung in verschiedenen Anwendungsfeldern umfasst als wesentlichen Komponenten die Beschreibung der Topologie und des dynamischen Prozessverhaltens mit Hilfe von partiellen und gewöhnlichen differential-algebraischen Gleichungssystemen. Die DSKP- und DSVP-Simulationsmodelle werden als örtlich diskretisiertes und zur numerischen Lösung geeignet umgewandeltes Gleichungssystem definiert. Infolge der örtlichen Diskretisierung ensteht eine sekundäre Topologie, die in der Modellumwandlung eine wichtige Rolle spielt und im Gleichungsgenerator berücksichtigt wird. Die DSKP- und DSVP-Modellierung ist ein Vorgang, der die Etappen der rechnergestützten Erstellung von Modellen und Simulationsmodellen sowie ihre Implementierung umfasst. Diese Etappen werden für die Topologien von verfahrenstechnischen Fließbildern, automatisierungs-technischen Strukturen und dynamischen Netzobjekten in Abb.1 dargestellt. Dabei wird vorausgesetzt, dass dem Modellentwickler in dem jeweiligen Anwendungsfeld eine hochentwickelte Benutzeroberfläche (BOF), ein Topologieanalysator sowie ein Gleichungsgeneratoren zur Verfügung stehen.
Die virtuelle parallele DSKP-, DSVP-Simulationsmodelle
Virtuelle parallele DSKP- und DSVP-Simulationsmodelle (VPSM) bilden eine Abstraktion, die aus dem vorverarbeiteten Gleichungssystem und der mit dem Parallelisierungsansatz erstellten Struktur von virtuellen MIMD-Prozessen besteht. Ein virtueller MIMD-Prozess ist ein weitgehend autonomes Programm, das dem Lösungsalgorithmus des Gleichungsteilsysteme entspricht und über eine Schnittstelle mit den benachbarten Prozessen kommuniziert. Die durch einen Kommunikationsgraphen dargestellte logische Verbindungen zwischen den virtuellen MIMD-Prozessen stellen ein virtuelles Verbindungsnetzwerk dar. Die minimale Körnigkeit der virtuellen Prozesse (VP) charakterisiert den Umfang der Prozess-Berechnungsarbeiten und die VP-Menge. Sie ist von der Dekomposition der Topologie und Modellgleichungen sowie der örtlichen DSVP-Approximation abhängig. Bei der Dekomposition und Approximation entstehen Teilsysteme, deren nicht zerlegbare Elementen diskretisiert werden. Deshalb wird vorgeschlagen, die minimale Körnigkeit der virtuellen Prozessen entsprechend der bei der Dekomposition und Diskretisierung hergeleitete Simulationsgleichungen zu definieren.
Die mit der minimalen VP-Körnigkeit verbundenen Ansätze zur DSKP- und DSVP-Parallelisierung führen auf die Parallelitätsebenen der virtuellen parallelen Simulationsmodelle.

Abb.1. Etappe der Erstellung von DSKP-, DSVP-Simulationsmodelle
Abb. 2 zeigt vier möglichen Parallelitätsebenen der dynamischen Netzobjekte (DNO) mit verteilten Parametern [1]. Nach der Auswahl der numerischen Verfahren werden die den Parallelisierungsansätzen und den Parallelitätsebenen zugeordneten virtuellen Simulationsmodelle und deren Blockdiagramme erstellt.
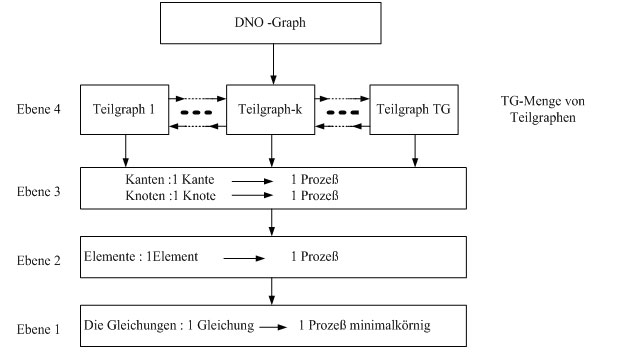
Abb. 2. Die VPSM-Parallelitätsebene für DNO-Topologien
Devirtualisierung von virtuellen parallelen Simulationsmodellen
Die Zielrechnerarchitektur ist die dem Modellentwickler zur Verfügung stehende lose oder/und eng gekoppelte, nach MIMD-Prinzip funktionierte, beschränkte heterogene Menge der installierten vollfunktionellen Prozessoren mit lokalem oder/und gemeinsamem Speicher und verfügbarem vordefiniertem programmgesteuertem Verbindungsnetzwerk. Als paralleler Simulator für das
betrachtete komplexe dynamische System wird eine Hardware/Software-Systemorganisation definiert, die den Modellierungsvorgang und paralleles virtuelles Simulationsmodell auf Zielrechnerarchitektur sofwaretechnisch effizient realisiert und den Modellentwicklern sowie den Modellbenutzern eine benutzerfreundliche Kommunikation mit den Modellierungs- und Simulationsressourcen erlaubt. Die benötigte Devirtualisierung von virtuellen parallelen Simulationsmodellen betrifft deren Umwandlung im Hinblick auf die Simulatorrealisierung mit Hilfe der vorgegebenen Zielrechnerarchitektur.
Hierzu werden die einzelnen Entwicklungsetappen des Devirtualisierungsvorgang auf parallelen DSKP- und DSVP-Simulatoren vorgeschlagen. Ausgangspunkt der Entwicklung ist eine detaillierte Darstellung der parallelen virtuellen Simulationsmodelle und Parallelitätsebenen. Die weitere Schritte sind die Apriori-Analyse und eine Optimierung der Lastverteilung zwischen den virtuellen Prozessen unter Berücksichtigung der Datenaustauschoperationen im Vergleich zu dem Umfang der Rechenoperationen.
Dabei werden die zur Implementierung geeigneten optimierten virtuellen Simulationsmodelle ausgewählt und deren Kommunikationsgraphen definiert. Außerdem werden die Struktur und das Blockdiagramm der devirtualisierten parallelen Simulationsmodelle mit den Parametern die Simulation der jeweiligen DSKP- und DSVP-Systeme befüllt. Schließlich werden die Implementierung und das Debugging des parallelen DSKP- und DSVP-Simulators untersucht.
Ein Anwendungsbeispiel
Die obige virtuelle Simulationsmodelle und ihre Devirtualisierung werden anhand der Beispiele aus des Gegenstandsgebiets „Grubenbewetterungssysteme“ betrachtet. Abb. 3 illustriert die Dekomposition und Ortsdiskretisierung des Grubenbewetterungssystems.

Abb.3. Dekomposition und Ortsdiskretisierung des Grubenbewetterungssystems
Die nach der Dekomposition erhaltene DNO-Komponenten haben folgende Eigenschaften, die wir für die weitere Parallelisierung in den Betracht nehmen sollen:
- alle Komponenten funktionieren kontinuirlich, also parallel und asynchron zu einander;
es besteht eine Energieabhängigkeit der Lufstromwerte von der Ventilatoren-charakteristiken; die Luftströme sind über Netz verbunden und haben Empfindlichkeit zur aerodynamischen Störungen, die in den beliebigen Punkten des Netzes entstehen können; diese Tatsache wird physikalisch in den Kanten- und Knotengleichungen berücksichtigt; die Ortsdiskretisierung von Komponenten gibt die finite Elemente, die zeitabhängig kontinuirlich bleiben und funktionieren parallel; die Kontinuität der Elementen, Komponenten und DNO insgesamt bedeutet einerseits eine inhärente Parallelität, verursacht aber andererseits enggekoppelte Berechnungsprozesse, die auf jeden Zeitschnitt der Datenaktualisierung von Nachbarelementen, Reglern, Ventilatoren, Störungsquellen sowie Knotenverbindungen brauchen.
Die luft- und gasdynamische Vorgänge in den Ventilationsabbauten und Ventilationsstrecken, in den Strebe, Förderstrecken und Luftzufuhrabbauten werden durch eindimensionale Modelle (partielle Differentialgleichungen) beschrieben. Die Ortsdiskretisierung nach Linienverfahren führt zur sekundären DNO-Topologien mit den Graphkanten, die jeweils aus Mi Elementen bestehen (i = 1,2,..., m). Jede Kante wird mit einem System der 2Mi gewöhnlichen Differenzialgleichungen (Differenzgleichungen bezüglich der Ortskoordinate) beschrieben. Um die minimale Körnigkeit der virtuellen Prozessen zu definieren, wurden die Gleichungssysteme aller in Abb. 3 dargestellten DNO-Komponenten analysiert und zur Betrachtungen folgende Prozesse eingefüurt:
1. Q-Prozeß dient für die numerische Lösung der Bewegungsgleichung des Elementes von diskretisierten DNO-Komponenten. Entsprechend der Bergbaubedingungen sind die 4 Varianten des Q-Prozesses zu unterscheiden: Q-Pro1 - die luftverlustlose Abbauten; Q-Pro2 - die Luftzufuhrstrecke mit den Luftverluste; Q-Pro3 - die Ventilationsstrecke mit den Luftzunahmen g1, g2 ; Q-Pro4 - die Luftströme in den Filtrationswege der Alten Männer (AM). Es gibt eine Möglichkeit diese Prozesse-Gleichungen zu generieren.
2. P-Prozeß dient für die numerische Lösung der Kontinuitätsgleichung des Elementes von diskretisierten DNO-Komponenten. Es sind auch die 4 Varianten des P-Prozesses für die obigen Bergbaubedingungen zu unterscheiden: P-Pro1, P-Pro2, P-Pro3, P-Pro4. Diese Prozesse sind auch generierbar.
3. PU-Prozeß dient für die numerische Lösung der Kontinuitätsgleichung in den DNO-
Knoten mit den inzidenten End- und Anfangselementen von diskretisierten DNO-Kanten. PU-Prozeß-Gleichungen werden vom DNOVP-Gleichungsgenerator generiert [1]
4. H-Prozeß berechnet Druck des Ventilators abhängig von entsprechenden Luftstrom
5. HN-Prozeß simuliert den HN-Regler, der die H-Charakteristik
abhängig von Drehzahl des Ventilatormotors im Arbeitsgebiet verschiebt
6. Q-Reg1-Prozeß simuliert den Q-Regler vom Qsoll -Eingang bis zum Ausgang des Motors
7. Q-Reg2-Prozeß simuliert den Q-Regler vom Antriebseingang bis zum Ausgang RR(t) des
Reglers
8. Cik-Prozeß dient für die Berechnung der Methankonzentration im k-Element der diskretisierten Strecken, Strebe und Luftausfuhrwege. Die Prozesse-Gleichungen sind als Cauchy-Aufgaben dargestellt und haben einige Unterschiede in den Rechten Seiten.
9. CG-Prozeß dient für die Berechnung der Randbediengung für i-Strecke bzw. Abbauten (G - Grenze).
10. QMk -Prozeß dient für die Berechnung der Methanströme in den k-AM-Elementen
11. Cfk-Prozeß berechnet die Methankonzentration in den Filtrationströme der k-AM-Elemente
Nach der Dekomposition und Ortsdiskretisierung des Bewetterungsnetzes mit m = 117 Kanten und n = 61 Knoten [1] geben diese Arten von Prozessen insgesamt mehr als 100000 Gleichungen, die das virtuelle parallele minimalkörnige Simulationsmodell auf erster Parallelitätsebene (Abb. 2) presentieren. Diese Gleichungen werden nach den Angaben des Topologieanalysators mit dem Gleichungsgenerator automatisch erstellt. Im Rahmen der problemorientierten parallelen Simulationsumgebung [1] wird den oben vorgeschlagenen Devirtualisierungsvorgang untersucht. In Betracht nehmen wir die folgende Zielrechnerarchitekture [2]: eng gekoppelte MIMD-Systeme mit dem gemeinsamen Adressraum und OpenMP-Standard der parallelen Programmierung; lose gekoppelte MIMD-Systeme mit verteiltem Adressraum und MPI-Standard des Nachrichtenaustausches; kombinierte parallele Rechnersysteme mit dem hybriden parallelen Programmiermodell [3]. Die Gleichungslösern des parallelen Simulators werden aufgrund der parallelisierten konventionellen sowie blockartigen numerischen Verfahren entwickelt [1].
Zusammenfassung und Ausblick
Die vorgestellten Ergebnisse liefern einen Beitrag für rechnergestützte Erstellung von Modellen, Simulationsmodellen und Simulatoren der dynamischen Systeme mit konzentrierten und verteilten Parametern, für die simulationstechnisch effiziente Nutzung der parallelen Ressourcen sowie für die Erhöhung der Benutzerfreundlichkeit von parallelen Simulationsumgebungen. Die vorgeschlagene virtuelle parallele Simulationsmodelle und Devirtualisierungsvorgänge werden in der Zusammenarbeit mit dem Höchstleistungsrechenzentrum Stuttgart (HLRS) implementiert und untersucht.
Literatur
1. Svjatnyj V.A., Moldovanova O.V., Feldmann L.P.: Parallele Simulationsumgebung für dynamische Netzobjekte mit verteilten Parametern. In: F.Hülsemann u.a. (Hrsg.), Tagungsband 18. ASIM-Symposium Simulationstechnik, Erlangen 2005, SCS 2005, 416-421.
2. Rabenseifner, R.: Parallel Programming Models on Hybrid Systems. In: Parallel Programming Workshop, HLRS, 2005.
3. Berger, H.: NEC SX-8 at HLRS. In: Parallel Programming Workshop, Interner Bericht Nr.5, HLRS, 2006.
|