Источник:http://www.techonline.com/article/pdf/showPDF.jhtml?id=2022016311

A New PLL Based Frequency Synthesis Technique

Kostas Efstathiou, El. Eng. Ph.D.
efstathiou@ee.upatras.gr
Applied Electronics Laboratory
Department of Electrical Engineering & Computer Technology
University of Patras
University Campus of Rio
26500 Patras, Greece.

Abstract

A new PLL based frequency synthesis technique is presented in this paper. The new technique is able to sample the phase of the reference and the output frequency at very high rate, in contrast to the conventional PLL based synthesizer that samples the phases of the two frequencies at a rate equal to the step frequency. The increased sampling rate of the phases, results to the increased convergence speed, and on the same time, to the elimination of the spurs nearby the output frequency. The resolution of the synthesizer can be significantly increased, without limiting the settling time and without affecting the quality of the output. Moreover, the behavior of the loop does not depended any more from the output frequency.

1. Introduction

The designer of the PLL based frequency synthesizer has to compromise the settling time, the resolution and the quality of the synthesized frequency. The main reason for this design trade- offs is the low sampling rate of the phase difference that is usually equal to the step frequency of the synthesizer. As the requirement for resolution increased, the sampling rate of the phase difference decreased, resulting to the above mentioned trade offs.

Several techniques have been developed to increase the performance of the PLL based synthesizer. As most popular can be considered the Fractional-N techniques [1], [2], [3], which however, cannot comply with the increased demands of the modern telecommunications. The Digital Direct Frequency synthesizers are used instead, on the penalty of the increased power consumption and the use of up-converters required to synthesize high frequencies.

In this paper we present a technique that breaks through the limitations of the conventional PLL based synthesizer. Applying this technique, the phase of the reference and the output frequency is sampled at very high rate and on the same time each phase is normalized and their difference is calculated. The high sampling rate of the phases of the two frequencies increases significantly the performance of the synthesizer that becomes comparable to this of the Digital Direct Frequency Synthesizer.

2. The Dual Input Phase Accumulator

According to the new technique, the Phase Frequency Detector (PFD) and the dividers of the reference and the output frequency of the synthesizer used in the conventional PLL based synthesizer, are substituted with a DUAL INPUT PHASE ACCUMULATOR (DIPA) [4]. Inputs to the DIPA are the two frequencies of the synthesizer (the reference and the output frequency) and two variables that normalize the phases of the two input frequencies and correspond to the numbers loaded to the dividers of the conventional synthesizer. The DIPA operates according the following rule:

At each period of the Reference Frequency, a value proportional to the Output Frequency is added to the accumulator, and at each period of the Output Frequency, a value proportional to the Reference Frequency is subtracted from the accumulator.

According to the rule the phase of each frequency is sampled every 360°(2π) and therefore, the sampling rate of the phase of each frequency is equal to the frequency itself.

2.1. The DIPA output

Let us examine the properties of the output of the DIPA assuming that the Reference Frequency (Fref) is 5 and the Output Frequency (Fout) is 7. According to the DIPA rule, the Reference Variable (Vref) should be 7 and the Output Variable (Vout) should be 5. The output of the DIPA and the phases of the two frequencies are depicted in Fig. 1.

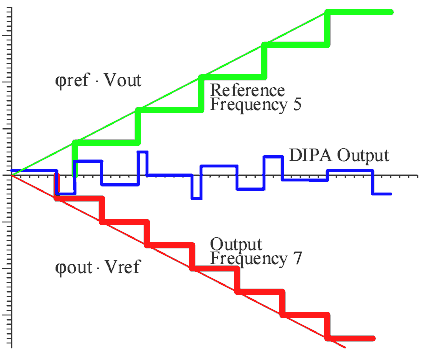
Figure 1. The output of the DIPA

The output of the DIPA due to the reference frequency is an up going staircase with a step- width equal to the period of the Reference Frequency and a step-height equal to the variable Vout. Consequently, the output of the DIPA due to the output frequency is a down going staircase with the corresponding characteristics.

Each staircase can be analyzed in two components:

• a ramp, with a slope proportional to the product of the phase of the frequency and the corresponding variable
• and a sawtooth waveform of the frequency that generates the staircase and an amplitude proportional to the corresponding variable

The subtraction of the two ramps is the phase difference of the normalized phases, while the subtraction of the two sawtooth waveforms can be considered as the noise due the sampling of the two phases. Thus, the output noise of the DIPA is derived by the subtraction of the two sawtooth waveforms as is depicted in Fig. 2. The sawtooth waveform has harmonics of the fundamental frequency. Therefore, the output noise of the DIPA consists of harmonics of the two high input frequencies, the reference frequency and the output frequency.

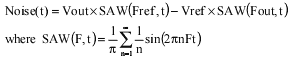
The filter of the loop has to reject these high frequencies, while the filter of the conventional synthesizer has to reject a low frequency, which is equal to the step frequency (Fstep) of the synthesizer. In most of the cases the step frequency is several thousand times lower than the reference and the output frequency. Therefore the bandwidth of the LPF can be increased significantly, increasing on the same time the bandwidth of the loop.

Additionally it should be mentioned, that since the DIPA output noise consists of high frequencies, it may required no filtering, since this noise will appear very far from the synthesized frequency, probably out of the useful band.

Figure 2. The DIPA's output noise

3. The Implementation of the DIPA

An implementation of the DIPA using digital technology can be found at [5]. The hardware requirements for the digital implementation do not demand a large amount of gates. A 16 bits DIPA has been implemented on a 2.5 thousands gates, low cost FPGA. The results derived by this implementation demonstrate the significant enhancements of the DIPA based FS. However the DIPA is able to be implemented using analog electronics.

The analog implementation of the DIPA is more attractive and challenging than the digital one, since it consumes less power, it can operate at higher frequencies, and requires significantly less circuitry. However the analog implementation suffers from the frequency error introduced by the imperfections of the analog components used.

The first approach of the analog DIPA [6] proves that the frequency error introduced due to the above-mentioned imperfections may not be significant. In this paper we propose an alternative analog implementation and we consider on the frequency error that introduces.

3.1. The analog DIPA

In Fig. 3 the analog DIPA is depicted. As it can be seen the Analog DIPA consists of two identical blocks and a current mirror. Each block consists of an Operational Amplifier, a voltage controlled current source and its current mirror, and a Frequency Depended Resistor (FDR). The Operational Amplifier controls the current source so as to keep the voltage applied on the FDR equal to its positive input. The current supplied to the FDR is measured by the mirror of the current source. The currents derived from the two blocks are subtracted with the aim of the middle current mirror. The use of the capacitor Co integrates the difference of the two currents.

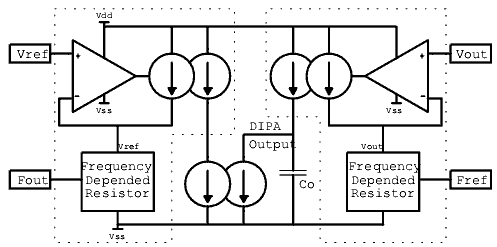
Figure 3. The Analog DIPA

Each FDR is a CMOS inverter with a small capacitor C at its output. The current flow through this inverter is depended on the supply voltage of the inverter, the frequency that it toggles and the capacitor. Thus, we can write the expression of the output of the DIPA. It can be seen that the output of the DIPA is proportional to the normalized phase difference of the two input frequencies.

Before studying the frequency error that introduces the DIPA, due to the use of non-ideal components, we have to study the behavior of a frequency synthesizer based on the ideal DIPA.

3.1.1 The DIPA in Blocks

Let us assign the gain of phase detector as Kd and the Voltage Ratio Vout over Vref as Kf.

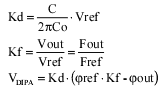
According to the equation of the DIPA, it incorporates a multiplier that multiplies the reference phase with the value Kf and an adder with gain Kd (given in volts per radius) that calculates the normalized phase difference. The block diagram of the DIPA is given in Fig. 4.

Figure 4. The DIPA in Blocks

3.1.2 The DIPA Based Synthesizer

The DIPA based synthesizer, depicted in Fig. 5, incorporates a Low Pass Filter (LPF) with a transfer function F(s) that rejects the DIPA’s noise, the VCO and of course the DIPA. Optionally, a prescaler may by used so as to scale the frequency of the VCO, down to a frequency that the DIPA can handle.

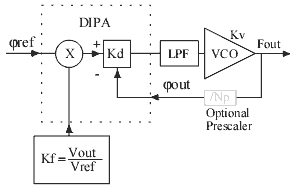
Figure 5. The DIPA based frequency synthesizer

It should be emphasized that the feedback of the loop is always constant and does not depended on the desired output frequency, as it does in the conventional FS. Therefore, the designer does not have to face any trade-off related to the behaviour of the loop and depending on the frequency range that the FS has to cover.

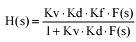
Assuming that the LPF is a lag filter, the parameters that control the behaviour of the loop are given:

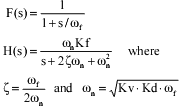
The second significant improvement of the frequency synthesizer based on the DIPA is, that the Low Pass Filter (LPF) of the loop, has to filter-out very high frequencies. Actually, it has to filter out the reference and the output frequency. Therefore, the designer is able to increase the bandwidth of the LPF and consequently the bandwidth of the loop, by a value equal to the ratio of the reference or the output frequency over the step frequency of the synthesizer. In conventional PLL based Frequency Synthesizer, this ratio is a number expressed in thousands. Thus, the bandwidth of the loop can be increased several thousands times. This, results to the increment of the convergence speed of the loop at the same value. Moreover, the increased bandwidth of the loop reduces significantly the phase noise of the synthesized frequency at a wide frequency range. Additionally, it should be emphasized that the output of the DIPA has not low frequency components related to the step frequency of the synthesizer. Thus, the spectrum nearby the synthesized frequency is clear.

Finally, the third significant improvement of the frequency synthesizer based on the DIPA is, that the increased resolution of the synthesized frequency does not affect the behaviour of the loop. The step frequency of the synthesizer is depended on the resolution of the variable Kf. Therefore the designer is able to increase the resolution of the synthesizer with out to worry about the convergence speed of the loop. Since Vout and Vref are voltages, it is able to achieve even linear resolution. The step frequency of the synthesizer is:

3.2 The Accuracy of the Analog DIPA based FS

The limited gain of the OpAmp affects the precision of the voltage applied on the FDR and consequently the accuracy of the synthesized frequency. In order to increase the accuracy of the synthesized frequency the OpAmps employed should have high gain and their gain should be matched.

This can be easily achieved if the OpAmps are build-in the same chip. However this requirement can be considered as a non-critical requirement, since the frequency error that introduces is not significant. For example, when the OpAmps have a gain of about 10.000 that is matched within 2%, they introduce a frequency error that is less than 2 parts per million (PPM).

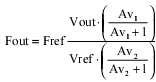
The frequency error introduced due to the DC Offset of the OpAmps is critical. It is probably the most significant problem of the analog DIPA.

Therefore, it is mandatory to use OpAmps with very low DC offset and additionally we have to apply DC Offset cancellation techniques. However it should be emphasized that this error is reduced as the reference over the output frequency ratio is closed to one.

3.2.2 Imperfections of the FDR

The FDR is a CMOS inverter that drives a capacitor. The current flows through the inverter should be equal to the current required to charge the capacitor. During the transition of the input, both MOSFETs of the inverter are on and a current flows through the MOSFETs to the ground. In order to eliminate this current we have to use the well known ‘Two Phase Clock Generator’ based on the NOR latch and depicted in Fig. 6.

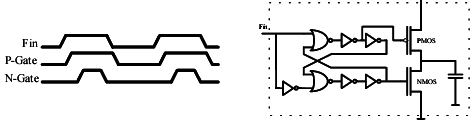
Figure 6. The FDR using a Two Phase Clock Generator

In order to eliminate further the FDR non-linearity, we use two FDRs, as is depicted in Fig. 7, where the first one drives, for example, a 2 pico-farads capacitor and the second one an 1 pico-farad capacitor. The current flow through the two FDRs consists of the current required to charge the capacitor and the current that introduces the non-linearity of the inverter. Subtracting the currents flow through the two FDS, the non-linear component is eliminated and remains the current required to charge a capacitor equal to the difference of the two capacitors used.

Figure 7. The FDR 'Compensation'

It has been found by simulations that the FDR with this type of ‘compensation’ introduces frequency error that can be as small as 50 parts per million over a wide frequency range. It also has been found this error decreases, as the size of the MOSFETs decreased and the difference of the two capacitors decreased. It should be emphasized that the FDR compensation is not mandatory when the ratio of the Reference over the Output frequency is close to one. The frequency error introduced in this case is negligible, since both FDRs have the about the same non-linearity.

4. Conclusions

The DIPA based Frequency Synthesizer and considerations on its analog implementation have been presented in this paper. It is apparent that the DIPA based synthesizer has a significantly enhanced performance. More specifically:

• The settling time can be extremely small.
• The resolution can be even linear.
• There are no spurs near by the synthesized frequency.
• The behavior of the loop is not depended on the synthesized frequency.
• and the phase noise is suppressed over a wide frequency range.

Obviously, the performance of the DIPA based synthesizer is superior and it is not fair to compare it with this of the conventional one.

The digital implementation of the DIPA does not suffer from the imperfection of the devices used. The synthesized frequency using the digital DIPA is extremely accurate, since the accuracy is only depended on a ratio of two digital words representing the variables Vout and Vref. The analog implementation is more attractive, however the imperfections of the analog devices employed for this implementation introduce a frequency error. More specifically the analog DIPA:

• is simple and can be implemented easily on a chip
• can operate at high frequencies
• has low power dissipation
• but it suffers from the Frequency Error.
• and requires very careful design and manufacturing

It is estimated that in short time and with the aim of the advanced IC technology, it will be able to obtain a very fast, very accurate analog DIPA. Therefore, we can foretell that the analog DIPA will become soon, the dominant frequency synthesis technique.

References

1. Gillette G. C., 1969, The Digiphase principle. Frequency Technology, Aug 1969, pp. 25- 29.
2. Wheatley E. Charles, 1983, Digital Frequency Synthesizer with random Jittering for reducing discreet spectral spurs. United State Patent No. 4,410,954.
3. Riley, Tom A.D.; Copeland, Miles A.; Kwasniewski, Tad A. 1993. Delta-Sigma modulation in fractional-n frequency synthesis. IEEE Journal of Solid-State Circuits. 28 No. 5, pp. 553-559.
4. K. A. Efstathiou, A., G. D. Papadopoulos, G. Kalivas, High Speed Frequency Synthesizer based on PLL, IEEE International Conference on Electronics, Circuits and Systems, Rodos, Oct. 1996, Vol. 2, pp. 627-630
5. K. A. Efstathiou, G. D. Papadopoulos, "Implementation of a High Speed Frequency Synthesizer employing a Dual Input Phase Accumulator", International Journal of Electronics, pp. 43-56, No. 1 Vol. 87, January 2000.
6. K. A. Efstathiou, A., G. D. Papadopoulos, "An Enhanced Frequency Synthesizer using an Analog Dual Input Phase Accumulator", Proceedings of the Sixth IEEE International Conference on Electronics, Circuits and Systems, Vol. 1, pp.17-20, Paphos, Cyprus, Sept. 1999.