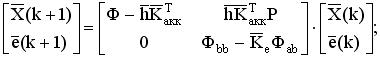СИНТЕЗ РЕГУЛЯТОРА ДИСКРЕТНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ЭЛЕКТРОМАГНИТНЫМ ПОДВЕСОМ ВЫСОКОСКОРОСТНОГО НАЗЕМНОГО ТРАНСПОРТА
Марьенков В.С., группа СУА – 07см
Руководитель доц. Рафиков Г.Ш.
Сборник научных статей студентов факультета "Компьютерных информационных технологий и автоматики". Выпуск 5. - Донецк: ДонНТУ. - 2007г.
Одной из основных составляющих инфраструктуры современного мира, бесспорно, является транспорт. Проблемы транспорта всегда оставались и остаются актуальными во всех странах мира. Основными направлениями развития транспорта в мире являются автомобильный, железнодорожный и авиа транспорт. Но как показывает опыт, эксплуатация этих видов транспорта показывает, что повышение скоростей передвижения неизбежно ведет к увеличению расходов, загрязнению окружающей среды и значительным зашумлением прилежащих районов.
Перспективной альтернативой обычному транспорту может оказаться бесколесный рельсовый транспорт. Распространено мнение, что его целесообразно использовать главным образом для скоростного междугородного наземного сообщения, однако этот вид транспорта может найти применение и в других областях, например в городских транспортных системах [1].
Как показали исследования, наиболее приемлемым является магнитный способ, т.е. использование системы с магнитной подвеской (МП) применительно к высокоскоростному наземному транспорту (ВСНТ).
Одной из наиболее сложных задач, решаемых при создании систем ВСНТ с электромагнитным подвесом (ЭМП), является проблема управления экипажем в пространстве с помощью системы автоматического регулирования зазора между полюсами электромагнита и феррорельсами [2]. Для обеспечения устойчивости и надежности ЭМП экипажа ВСНТ используют различные комбинации сигналов обратных связей по зазору, скорости и ускорению изменения зазора. Система также должна учитывать малое значение зазора (около 10 мм), следовательно должна работать с большой точностью.
Структурная схема системы ЭМП ВСНТ представлена на рис. 1.
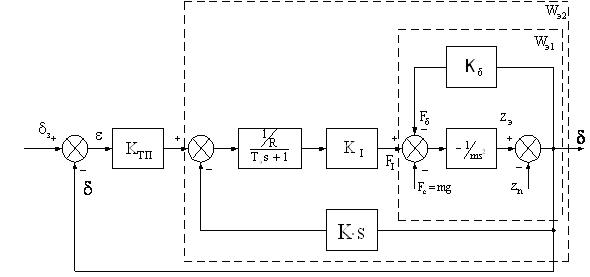
Рисунок 1 – Структурная схема системы автоматического регулирования зазора
На рис. 1 введены следующие обозначения:
 – воздушный зазор между полюсами электромагнитов и феррорельсом;
– воздушный зазор между полюсами электромагнитов и феррорельсом;
 – сигнал рассогласования;
– сигнал рассогласования;
 – координата электромагнита;
– координата электромагнита;
 – координата пути;
– координата пути;
Тэ – постоянная времени электромагнита (ЭМ);
R – сопротивление ЭМ;
m – масса экипажа;
Kтп – коэффициент усиления вентильного преобразователя;
 – коэффициенты передачи соответственно от тока и зазора к силе;
– коэффициенты передачи соответственно от тока и зазора к силе;
K – коэффициент передачи от скорости изменения зазора к ЭДС индукции.
По структурной схеме определяем передаточную функцию разомкнутой системы по регулируемой величине  , в результате получаем:
, в результате получаем:
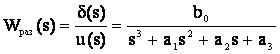
где 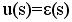 – изображение управляющего воздействия в виде сигнала рассогласования, поступающее на вход системы.
– изображение управляющего воздействия в виде сигнала рассогласования, поступающее на вход системы.
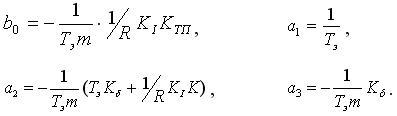
Исходными численными значениями параметров рассматриваемой системы являются: m=22500 кг, R=175 Ом, TЭ=4,5 с, KТП=4500 В/В, KI=7200 Н/А, 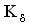 =22.5•103 Н/м, K=2160 В•с/м.
=22.5•103 Н/м, K=2160 В•с/м.
Алгоритм синтеза динамического регулятора состоит в следующем, от передаточной функции перейдем к дифференциальному уравнению:
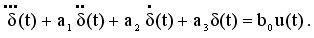
Далее переходим к описанию системы в пространстве состояний. После чего проводим дискретизацию системы с помощью разложения в ряд матричного экспоненциала по формуле:
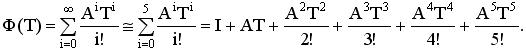
Далее вычислим вектор управляемого перехода 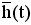 по формуле
по формуле
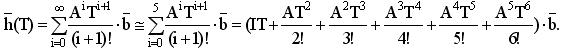
Синтез модального регулятора и наблюдателя пониженного порядка производится на основе желаемого размещения полюсов дискретной динамической системы с использованием метода Аккермана [3]. Коэффициенты обратной связи регулятора ищем по формуле:
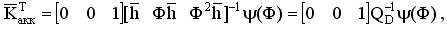
Где 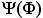 – полиномиальная матрица замкнутой системы.
– полиномиальная матрица замкнутой системы.
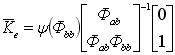
Коэффициенты обратной связи наблюдателя пониженного порядка ищем по формуле:
В результате синтеза получаем математическую модель дискретной динамической системы в пространстве состояний. Обобщенное уравнение системы, учитывающее модальный регулятор и наблюдатель состояния пониженного порядка имеет следующий вид:
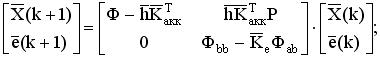
Для облегчения вычислений и автоматизации моделирования процесса используется пакет прикладных программ Matlab [4].
Для исследования полученной модели используем варьирование параметров исходной динамической системы (Тэ, KТП, KI, 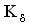 и K). Варьируя параметры в пределах ±20% получаем переходные процессы в системе.
и K). Варьируя параметры в пределах ±20% получаем переходные процессы в системе.
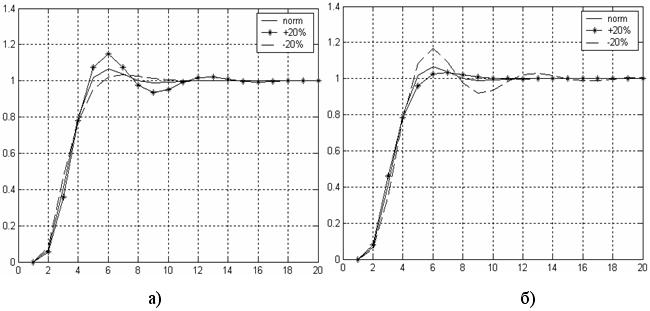
Рисунок 2 – Реакция замкнутой ДДС на единичный скачок при отклонении значения Тэ (рис. 2 а) и KI(рис. 2 б) на ±20% от номинального значения.
В результате анализа экспериментального моделирования можно сделать вывод о том, что наиболее чувствительными параметрами в системе электромагнитного подвеса при изменении на ±20% являются постоянная времени электромагнита Тэ и коэффициент передачи от тока к силе - KI. Остальные параметры практически не чувствительны к их изменению. При увеличении постоянной времени электромагнита и уменьшении коэффициента передачи от тока к силе, в системе исчезает перерегулирование, уменьшается время переходного процесса. Переходный процесс в системе завершается за 0,25 с, что говорит о высоком быстродействии системы.
Выводы по работе:
Получена математическая модель в виде передаточной функции исследуемой системы.
Вычислено описание системы в пространстве состояний.
Синтезирован динамический регулятор на основе желаемого размещения полюсов замкнутой системы по методу Аккермана.
Проведено моделирование исследуемой ДДС и получены переходные процессы в номинальном и возмущенном режимах работы.
Исследовано влияния измененных параметров на переходные процессы в системе.
Перечень ссылок.
Черноморец М. «Системы рельсового транспорта» в рамках Интернет-проекта «Earth-21» /Электронный ресурс. Способ доступа: URL: http://railwayhistory.iatp.org.ua
Режко Н.А. Системы управления электромагнитным подвесом. В кн. Высокоскоростной наземный транспорт с линейным приводом и магнитным подвесом. Под. Ред. В.И. Бочарова и В.Д. Нагорского. – М.: Транспорт, 1985. 273 с.
Katsuhiko Ogata. Designing Linear Control System With MATLAB. Printice – Hall, I no Engliwood Cliffs № I07630. – 1994 – 226 p.
Медведев В.С., Потемкин В.Г. Control System Toolbox. MATLAB 5 для студентов/ Под общ. Ред. К.т.н. В.Г. Потемкина. – М.: ДИАЛОГ – МИФИ, 1999 – 278 с.

 В начало
В начало








 – воздушный зазор между полюсами электромагнитов и феррорельсом;
– воздушный зазор между полюсами электромагнитов и феррорельсом; – сигнал рассогласования;
– сигнал рассогласования; – координата электромагнита;
– координата электромагнита; – координата пути;
– координата пути; – коэффициенты передачи соответственно от тока и зазора к силе;
– коэффициенты передачи соответственно от тока и зазора к силе;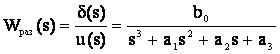
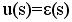 – изображение управляющего воздействия в виде сигнала рассогласования, поступающее на вход системы.
– изображение управляющего воздействия в виде сигнала рассогласования, поступающее на вход системы.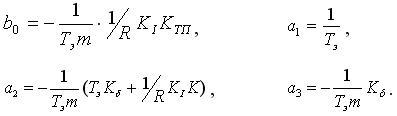
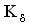 =22.5•103 Н/м, K=2160 В•с/м.
=22.5•103 Н/м, K=2160 В•с/м.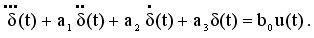
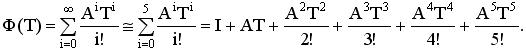
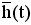 по формуле
по формуле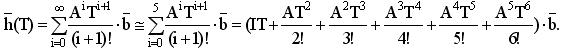
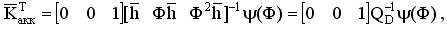
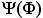 – полиномиальная матрица замкнутой системы.
– полиномиальная матрица замкнутой системы.