Коваленко В.И., Федосов Н.Н., Свистун Т.В. (ДонНТУ, г.Донецк, Украина)
Подготовлена к печати: Прогресивні технології і системи машинобудування: Міжнародний збірник наукових праць.- Донецьк: ДонНТУ, 2008.- Вип.33
Обзор состояния вопроса.
Проблема точности отверстий, получаемых осевыми режущими инструментами, в том числе сверлами, является актуальной. Уже на стадии проектирования инструмента в ряде случаев необходимо рассчитать величину возможной погрешности, вызываемой инструментом во время работы. Для рациональной
эксплуатации осевого режущего инструмента, в частности сверл, требуется их расчет на прочность, а в некоторых случаях (например, при сверлении глубоких отверстий) – также и на устойчивость [1].
При расчете сверл на прочность и устойчивость необходимо знание, в частности, сил резания (определяются по общемашиностроительным справочникам [2] или по специальным методикам [1]) и площадей поперечного сечения сверла. В известной литературе [3 - 5] подобные расчеты выполнены только для сверл,
имеющих наиболее употребительные конструктивные характеристики. В то же время в зависимости от конкретных условий обработки могут использоваться нестандартные сверла с конструктивными характеристиками, отличающимися от наиболее употребительных; в этом случае требуется точное определение площади поперечного сечения сверл.
Целью работы является определения площади поперечного усиленного сечения сверл, имеющих различные конструктивные особенности. Для достижения поставленной цели необходимо решить следующие задачи: определить площадь поперечного усиленного сечения сверл при постоянном отношении радиуса сердцевины сверла к радиусу сверла; определить площадь поперечного усиленного сечения сверл при изменении расчетного сечения от вершины сверла к хвостовику, определить поправочный коэффициент для определения площади поперечного сечения сверла.
Определение площади поперечного усиленного сечения сверла.
В отличии от поперечного сечения обычного спирального сверла [1], форма стружкоотводящих канавок которого образована пересечением окружностей со смещенными центрами относительно центра сверла и прямыми, образующими ленточку сверла, усиленное сечение сверла имеет более простую форму (рис.1) за счет того, что прямая стружкоотводящей канавки, получена при перпендикулярном пересечении плоскостью оси сверла и образует угол α с осью ординат.
Таким образом площадь усиленного сверла более прочная, что позволяет использовать сверла с таким поперечным сечением для обработки труднообрабатываемых материалов.
Данное различие несколько упрощает расчет поперечного усиленного сечения сверла, в сравнении с расчетом площади поперечного сечения обычного спирального сверла [1].
По рекомендациям [2] (рис. 1) при радиусе сердцевины rc = 0,2·r сверло усиленного сечения имеет следующие геометрические размеры: прямая стружкоотводящей канавки, получаемая при перпендикулярном пересечении плоскостью ось сверла, образует угол с осью ординат α = 12,011° и имеет в двухмерной системе координат следующую зависимость:
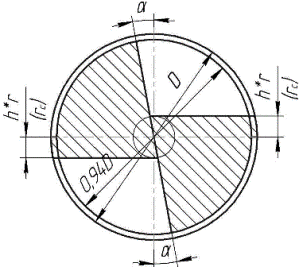
Рис. 1. Общий вид поперечного усиленного сечения сверла
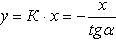 (1)
(1)
Для упрощения определения площади поперечного усиленного сечения сверла найдем зависимость изменения угла наклона α от изменения величины радиуса сердцевины.
Исследуем следующий диапазон значений коэффициента радиуса сердцевины h = 0 ÷ 1.
Сделаем следующие допущения:
- величина α изменяется в зависимости от величины радиуса сердцевины по квадратичному закону;
- при h = 1: α = 0°;
- при h = 0: α = 13,513°.
Тогда, учитывая [1] найдем взаимосвязь между коэффициентом радиуса сердцевины и α:
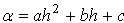 (2)
(2)
Найдем коэффициенты а, b и с.
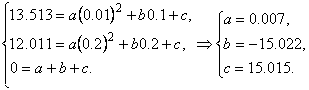 (3)
(3)
Тогда
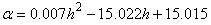 (4)
(4)
Площадь поперечного усиленного сечения спирального сверла относительно осей Х – Х и Y – Y определяется по следующим зависимостям:
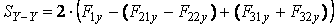 (5)
(5)
где F1y, F21y, F22y, F31y, F32y – площади простых фигур; F1y, F31y, F32y имеют такие же зависимости, как и для поперечного обычного сечения сверла, F21y, F22y определяются по следующим зависимостям (рис. 2 а):
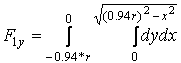 (6)
(6)
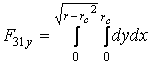 (7)
(7)
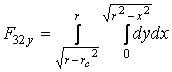 (8)
(8)
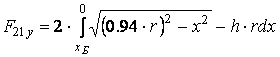 (9)
(9)
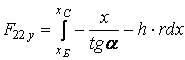 (10)
(10)
где хБ, хС – абсциссы точек Б(хБ; yБ) и С(хС; yС) пересечения прямой стружкоотводящей канавки с окружностью радиусом 0.94∙r и прямой y = h∙r.
По оси X – X площадь поперечного усиленного сечения спирального сверла определяется как сумма простых геометрических фигур по формуле (11). В этой зависимости F1х, F3х определяются так же, как и для поперечного обычного сечения сверла по (12) и (13),а F21х, F22х определяются по следующим формулам (рис. 2 б):
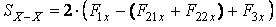 (11)
(11)
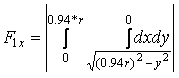 (12)
(12)
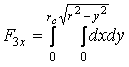 (13)
(13)
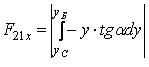 (14)
(14)
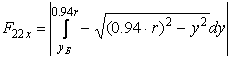 (15)
(15)
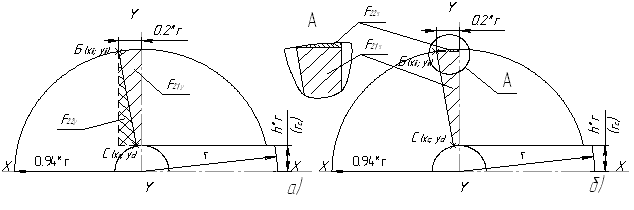
Рис. 2.Схема расчета площади поперечного усиленного сечения спирального сверла: а) – для нахождения площади отдельных частей F21y, F22y; б) – для нахождения F21х, F22х
Определение поправочного коэффициента для определения площади поперечного сечения сверла.
Найдем поправочный коэффициент kS для определения площади поперечного обычного и усиленного сечения сверла.
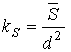 (16)
(16)
где 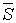 - средняя алгебраическая расчетная площадь сверла:
- средняя алгебраическая расчетная площадь сверла:
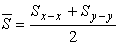 (17)
(17)
d – диаметр сверла.
Сравним поправочные коэффициенты для определения площади поперечного обычного и усиленного сечения сверл для чего совместим графики кривых на одном графике (рис. 3). По графику видно, что поправочный коэффициент несколько больше для усиленного поперечного сечения сверла, а значит и его площадь тоже больше.
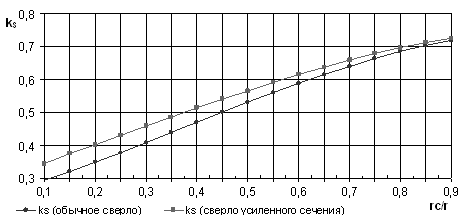
Рис. 3. Сравнение значений поправочного коэффициента для определения площади поперечного обычного и усиленного сечения сверл
По [2] при радиусе сердцевины rc/r = 0.2 поправочный коэффициент для определения площади поперечного сечения обычного сверла kst = 0.38, а для усиленного сверла kst = 0.4.
Поправочные коэффициенты для определения площади поперечного сечения, рассчитанные по приведенным выше зависимостям при том же радиусе сердцевины равны для обычного сверла ks = 0.348, для усиленного сверла ks = 0.402.
Определим погрешности, возникшие при вычислениях площади поперечного сечения сверла:
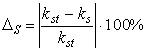 (18)
(18)
Погрешность при вычислениях поправочного коэффициента для обычного сверла составляет 8.5%, а для усиленного – 0.5%.
Такие погрешности возможны по следующим причинам:
- допущения, принятые в данной методике;
- округления в расчетах, выполненных по предложенной методике для определения площади поперечного сечения сверла.
Если допустить верность перечисленных причин, то при расчетах площади поперечного сечения необходимо учитывать и эти погрешности поправочных коэффициентов и определять площадь по следующей зависимости:
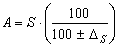 (19)
(19)
где А – откорректированное значение площади поперечного сечения сверла.
Знак "-" принимаем при расчете площади поперечного сечения обычного сверла, т.к. расчетные значения поправочного коэффициента для определения площади поперечного сечения получаются меньше, чем приведенные в литературе и потому увеличиваем его значение; знак "+" – при расчете площади поперечного сечения усиленного сверла, т.к. в этом случае расчетные значения поправочного коэффициента получаются больше, чем приведенные в литературе и потому уменьшаем его значение.
Сделаем следующие допущения:
- изменение значения погрешности ΔS имеет линейный характер;
- при rc/r → 1: ΔS → 0.
Тогда найдем эту зависимость изменения погрешностей при расчетах поправочных коэффициентов для определения площади поперечного сечения обычного и усиленного сверл от значения радиуса их сердцевин, общий вид которой:
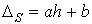 (20)
(20)
Найдем коэффициенты а и b для обычного сверла:
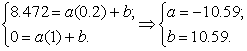 (21)
(21)
Тогда зависимость, по которой изменяется погрешность поправочного коэффициента для обычного сверла, имеет следующий вид:
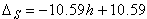 (22)
(22)
Найдем коэффициенты а и b для усиленного сверла:
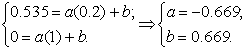 (23)
(23)
Тогда зависимость, по которой изменяется погрешность поправочного коэффициента для усиленного сверла, примет следующий вид:
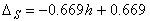 (24)
(24)
Выводы. С помощью рассчитанных выше поправочных коэффициентов можно легко определить площадь поперечного обычного и усиленного сечения сверла. Для этого необходимо иметь значения диаметра сверла и радиуса его сердцевины. Результаты выполненной работы дают возможность быстро определить площадь поперечного сечения сверл, с любым радиусом сердцевины, и тем самым не затрудняясь промежуточными расчетами, рассчитывать сверла на прочность и устойчивость, это намного ускорит и облегчит рациональный выбор режущего осевого инструмента.
Список литературы:
1. Коваленко В.И., Федосов Н.Н. Определение площади поперечного сечения сверла. Прогресивні технології і системи машинобудування: Міжнародний сб. наукових праць. – Донецьк: ДонНТУ, РВА ДонНТУ, 2007. - Вип. 33. С. 117-123.
2. Справочник технолога-машиностроителя. В 2-х т. Т. 2. Под ред. А.М. Дальского. - М.: Машиностроение -1, 2001. - 944 с.
3. Сопротивление материалов/Под ред. Писаренко Г.С. – 5-е изд. – К: Вища шк. Головное изд-во, 1986. – 775с.
4. Проектирование металлорежущих инструментов./ Под ред. И.И. Семенченко. – М: Машиностроение, 1963. – 895с.
5. Пономарев С.Д. Основы современных методов расчета на прочность в машиностроении./ М: Машгиз, 1952. – 864с.


