Малышко И.А., Коваленко В.И., Федосов Н.Н. (ДонНТУ, г.Донецк, Украина)
Прогресивні технології і системи машинобудування: Міжнародний сб. наукових праць. – Донецьк: ДонНТУ, 2006. - Вип. 31. С. 197 - 203.
Определение оптимальных режимов резания является одной из наиболее часто встречающихся задач при разработке различных технологических процессов механической обработки заготовок. От правильно рассчитанных режимов резания зависят такие характеристики механической обработки заготовок, как стойкость режущего инструмента, производительность обработки, технологические затраты и другое.
Вопросами расчета оптимальных режимов резания при сверлении длительное время занимаются различные исследователи [1 - 4]. Обобщающие рекомендации по определению режимов резания приведены в справочнике [5]. Однако, из-за различных исходных условий обработки и намеченных целей оптимизации процесса резания возникают разные варианты постановки этой задачи.
Целью настоящей работы является постановка задачи оптимизации режимов резания при сверлении аналитическим методом с учетом основных технических ограничений, накладываемых на процесс обработки.
В задачах расчёта оптимальных режимов резания входные параметры разделяют на искомые (управляемые) и заданные(неуправляемые). Задача оптимизации сводится к отысканию такого сочетания значений управляемых параметров, при котором, при заданных значениях неуправляемых параметров, совокупность выходных параметров является наилучшей (имеет экстремум).
В качестве искомых параметров при расчёте режимов резания обычно принимают скорость резания V и подачу S; глубина резания при сверлении однозначно определяется размером режущего инструмента и, следовательно, не может выступать в качестве искомого параметра.
Набор искомых параметров может быть представлен в виде некоторого множества X={x1,x2}. Тогда задача расчёта оптимального режима резания сводится к задаче математического программирования:
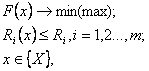
гдеF(x) - зависимость для принятого критерия оптимальности; x - искомый параметр из некоторого множества X; Ri(x) - значение i-ой характеристики процесса резания; Ri-заданное предельное значение i-ой характеристики процесса резания.
В качестве первого технического ограничения режима обработки при сверлении принимаем ограничение скорости резания, накладываемое кинематикой станка.
С одной стороны, скорость резания при сверлении обусловлена принятой стойкостью инструмента, материалом режущей части инструмента, его геометрией, глубиной резания, подачей, механическими свойствами обрабатываемого материала; значение скорости резания при этом определяется по справочнику [5] по общеизвестной формуле. С другой стороны, скорость резания определяется кинематической схемой станка (частотой вращения шпинделя n). Приравнивая выражения для определения скорости резания, подсчитанные с учетом вышеназванных обстоятельств, получим выражение для первого технического ограничения
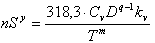 (1)
(1)
где Cv - постоянный коэффициент, характеризующий нормативные условия обработки; D - диметр инструмента, мм; Kv - общий поправочный коэффициент на скорость резания; T - принятая стойкость инструмента, мин; m - показатель относительной стойкости; q - показатель степени при D.
Второе техническое ограничение – это ограничение по мощности электропривода главного движения станка. Для нахождения аналитического выражения для этого ограничения определяют, с одной стороны, по справочнику [5] крутящий момент на шпинделе станка, возникающий вследствие наличия окружной силы резания при сверлении; с другой стороны, определяют крутящий момент на шпинделе станка, соответствующий мощности электродвигателя главного привода станка и числу оборотов шпинделя.
Учитывают, что крутящий момент вследствие возникающих усилий резания должен быть меньше крутящего момента, развиваемого станком по мощности установ-ленного на нем электродвигателя, то есть
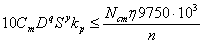 (2)
(2)
где Сm - постоянный коэффициент, учитывающий влияние на усилие резания обрабатываемого материала и других условий обработки; Кр - общий поправочный коэффициент, учитывающий условия обработки; q, y - показатели степеней соответственно при D, S; Nст - мощность электродвигателя главного привода станка, кВт;  - коэффициент полезного действия передачи от электродвигателя главного привода до инструмента.
- коэффициент полезного действия передачи от электродвигателя главного привода до инструмента.
Преобразуя неравенство (2), получаем
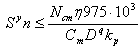 (3)
(3)
Полученное неравенство (3) устанавливает связь между силами резания при сверлении и мощностью электродвигателя главного привода станка и является одним из основных технических ограничений при определении оптимальных режимов резания.
Третье техническое ограничение устанавливает взаимосвязь искомых параметров и производительности станка Q, которая может быть определена как величина, обратная циклу работы станка Tц.
Производительность станка определяется из выражения
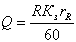 (4)
(4)
где R - теоретическая производительность станка, шт/ч.; Кз - коэффициент загрузки станка; rR - число деталей, одновременно обрабатываемых на одной позиции.
Продолжительность цикла работы станка Тц = 1/Q , или
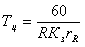 (5)
(5)
Время цикла определяется по формуле
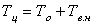 (6)
(6)
где То - основное технологическое время, мин; Тв.н - вспомогательное неперекрываемое время, мин.
Основное технологическое время определяется по формуле
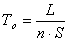 (7)
(7)
где L - длина рабочего хода инструмента.
Сравнивая уравнения (5) и (6) и учитывая, что время цикла работы станка долж-но быть больше времени цикла, определяемого суммой (Т0+Тв.н) получаем следующее неравенство
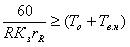 (8)
(8)
Подставляя в неравенство (8) значение Т0 из выражения (7) и решив его, получим третье техническое ограничение
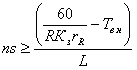 (9)
(9)
Четвертое техническое ограничение устанавливает взаимосвязь между усилием подачи Ро, действующим при резании на инструмент, и усилием подачи станка Pпод.ст., допускаемого прочностью механизма подачи станка.
Усилие подачи Ро, действующее на инструмент (определяемое по справочнику [5]), не должно превышать усилие подачи станка Pпод.ст.
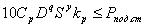 (10)
(10)
Полученное неравенство является одним из основных неравенств при определе-нии оптимальных режимов резания. Представим его в виде
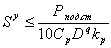 (11)
(11)
Пятое и шестое технические ограничения основаны на том, что полученное рас-четное значение частоты вращения шпинделя n должно находиться в диапазоне (min - max) частот, определяемых кинематикой станка (по минимумуnст.min и по максимуму nст.max ), или:
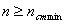 (12)
(12)
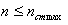 (13)
(13)
Седьмое и восьмое технические ограничения по своей структуре аналогичны двум предыдущим и устанавливают взаимосвязь расчётной величины подачи S с подачей, допустимой кинематикой станка (по минимумуSст.min и по максиму Sст.max ):
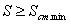 (14)
(14)
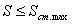 (15)
(15)
Так как в качестве критерия оптимизации будет использоваться минимальная себестоимость обработки, рассмотрим структуру себестоимости обработки детали на станке. Технологическая минутная себестоимость детали, то есть себестоимость детали, отнесенная к 1 мин работы станка, может быть определена из выражения
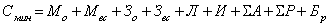 (16)
(16)
где Мо и Мвс - затраты на основные и вспомогательные материалы; Зо и Звс – за-работная плата основных и вспомогательных рабочих; Л – затраты на электроэнергию для технологических целей; И – затраты на инструмент и малоценные приспособления; 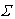 А – затраты на амортизационные отчисления от оборудования, технологического оснащения и производственных площадей;
А – затраты на амортизационные отчисления от оборудования, технологического оснащения и производственных площадей; 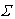 Р – затраты на ремонт оборудования, на ремонт и обслуживание систем управления; Бр – потери на технологический брак.
Р – затраты на ремонт оборудования, на ремонт и обслуживание систем управления; Бр – потери на технологический брак.
Приведенная себестоимость (на единицу пути инструмента)
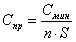 (17)
(17)
Принимаем, что при изменении режимов резания изменяется главным образом составляющая Спр , зависящая от затрат на электроэнергию для технологических целей; остальные составляющие от режимов резания не зависят, то есть остаются постоянными. В этом случае приведенная себестоимость определяется как
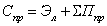 (18)
(18)
где Эл – приведенные удельные затраты на технологическую электроэнергию; 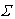 Ппр - приведенные удельные затраты от остальных элементов технологической себестоимости;
Ппр - приведенные удельные затраты от остальных элементов технологической себестоимости; 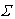 Ппр = const.
Ппр = const.
Приведенные удельные затраты на технологическую электроэнергию
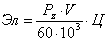 (19)
(19)
где Pz – тангенциальная составляющая силы резания; V – скорость резания; Ц – цена 1 кВт•ч электроэнергии. Элементы приведенной себестоимости определяются по нормативным документам [5]:
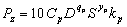 и
и 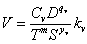
После подстановки значений Pz и V в выражение (19), преобразуем это уравнение таким образом, чтобы оно было представлено сомножителями, не зависящими и зависящими от подачи:
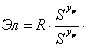 или
или
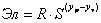 (20)
(20)
где R – часть приведенных удельных затрат на технологическую электроэнергию, не зависящая от подачи.
Покажем, что для конкретных условий обработки значение S(yp-yv) может быть близким к единице. Например, при обработке отверстий в конструкционной стали показатели степени при S равны [5]: yр=0,8 ; yv=0,7. При этом получаем численные значения вышеуказанного выражения: например, для S = 0,2 мм/об - S(yp-yv) = 0,20,1 = 0,85; для S = 0,5 мм/об - S(yp-yv) = 0,50,1 = 0,93.
С учетом вышеизложенного примем, что уравнение оценочной функции (критерия оптимальности) для минимальной себестоимости операции имеет следующий вид
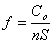 (21)
(21)
где Co – постоянная величина, не зависящая от режимов резания n, S.
Входящая в вышеприведенные уравнения и неравенства величина S в ряде случаев имеет значения порядка 0,01 - 0,1 мм, то есть этим значениям будут соответствовать отрицательные логарифмы. Для того чтобы избежать появления отрицательных логарифмов, умножим во всех уравнениях и неравенствах технических ограничений величину S на 100 и проведём соответствующие преобразования.
Прологарифмируем левые и правые части выше полученных уравнений и нера-венств, причем для удобства будем пользоваться натуральными логарифмами.
Введём следующие обозначения:
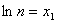
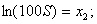
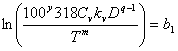
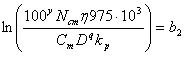
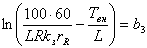
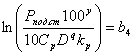
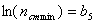
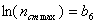
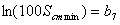
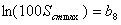
Подставляя введенные обозначения в полученные ранее уравнения и неравенства технических ограничений и критерия оптимальности, получим смешанную систему (А) линейных уравнений и неравенств и линейную функцию, подлежащую оптимизации:
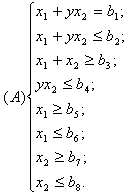
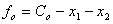 (22)
(22)
Смешанная система (А) линейных уравнений и неравенств и линейная функция fo в их совокупности представляют математическую модель (W) оптимального режима резания для одноинструментальной обработки на сверлильном станке. Полученная таким образом математическая модель W представляет собой универсальную теоретическую математическую модель оптимального режима резания.
Смешанная система (А) характеризует основные технические ограничения, в рамках которых протекает процесс резания. В том числе линейная форма уравнения (22) характеризует часть производительности операции, зависящую от режима резания.
Таким образом, задача определения оптимального режима резания математически сводится к тому, чтобы среди всевозможных неотрицательных решений x1,x2 системы (А) найти такие значения x1опт,ч2опт при которых линейное выражение (22) принимает наименьшее возможное значение.
Результаты этой работы представляют собой аналитическую модель оптимиза-ции режимов резания по критерию минимальной себестоимости. Пример реализации этой задачи будет выполнен в последующих исследованиях.
Список литературы:
1. Филоненко С.Н. Резание металлов. - Киев: Вища школа, 1969. – 260 с.
2. Макаров А.Д. Оптимизация процессов резания. – М.: Машиностроение. 1976. – 278 с.
3 Кроль О.С., Хмелевский Г.Л. Оптимизация и управление процессом резания. – К.УМК ВО,1991. – 140 с.
5. Справочник технолога-машиностроителя. В 2-х т. Т. 2. Под ред. А.М. Дальского. - М.: Машиностроение -1, 2001. - 944 с.


