Малышко И.А., Коваленко В.И. (ДонНТУ, г.Донецк, Украина)
Прогрессивные технологии и системы машиностроения: Международный сб. научных трудов. – Донецк: ДонНТУ, 2003, Вып. 24. С. 82 - 88.
Изучению процесса резания при сверлении посвящены многие исследования, в частности, [1 - 3]. Однако, в этих трудах процесс сверления рассматривается, в основном, с точки зрения физики самого процесса.
Целью работы является выявление взаимосвязи между силовыми и геометрическими параметрами процесса сверления, а также влияния точ-ности изготовления режущего инструмента на характер возникающих сил резания. В работе поставлена задача: выявить влияние взаимоотношения между точностью инструмента и принятой подачей на характер процесса резания при сверлении.
На основании выполненных раннее исследований [4] установлено, что наличие погрешностей заточки вызывает появление неуравновешенной радиальной силы резания Δ Py , оказывающей влияние на точность обработки отверстий при сверлении. Расчеты показывают, что колебания Δ Py соизмеримы с величиной радиальной составляющей силы резания Py на одной режущей кромке, а иногда могут быть равны этой силе.
В работе рассмотрено влияние величины погрешности заточки сверла на возникновение и величину неуравновешенной радиальной силы резания.
При симметричной заточке сверла исходное положение его режущих кромок AoAo и CoCo (рис. 1а) также симметрично. При повороте сверла (с рабочей подачей) на 180° режущие кромки сместятся в осевом направлении на величину подачи на зуб sz=0,5s , где s - подача сверла, и займут положение A1A1 и C1C1. При этом толщина среза ao для каждой из режущих кромок может быть найдена из треугольника EFG по выражению
ao=szsin (1)
(1)
где  - главный угол в плане. Так как снимаемые каждой режущей кромкой толщины среза равны, то и действующие на кромки радиальные силы резания Py также равны между собой и результирующая этих сил резания равна нулю. Таким образом, для случая симметричной заточки сверла величина неуравновешенной радиальной силы резания Δ Py = 0.
- главный угол в плане. Так как снимаемые каждой режущей кромкой толщины среза равны, то и действующие на кромки радиальные силы резания Py также равны между собой и результирующая этих сил резания равна нулю. Таким образом, для случая симметричной заточки сверла величина неуравновешенной радиальной силы резания Δ Py = 0.
В реальной практике металлообработки режущие кромки сверла всегда асимметричны. Согласно нормативным данным [5] регламентированы следующие значения допуска осевого биения режущих кромок сверл, приведенные в табл. 1; наличие указанного осевого биения вызывает появление неуравновешенной радиальной силы.
Таблица 1 - Допуск осевого биения режущих кромок сверл
| Вид сверла |
Диаметр сверла, мм |
Допуск, мм |
| Точное исполнение |
Общее назначение |
Быстрорежущие |
До 6 |
0,05 |
0,12 |
| 6-10 |
0,10 |
0,18 |
| Св. 10 |
0,20 |
0,30 |
| Оснащенные пластинами из твердого сплава |
5-10 |
0,06 |
0,12 |
| Св. 10 |
0,08 |
0,15 |
| Цельные твердосплавные |
1-3 |
0,02 |
0,04 |
| Св. 3-12 |
0,04 |
0,06 |
Следует отметить, что с точки зрения величины неуравновешенной силы резания имеет значение не только абсолютная величина погрешности заточки, но и ее относительное значение (по сравнению с величиной подачи на зуб, реализуемой на станке). Анализ показал, что существующие нормативы осевого биения зубьев могут превосходить величину подачи на зуб сверла.
Рассмотрим определение толщины среза для такого случая, когда при использовании сверл общего назначения величина осевого биения сверла Bo не меньше значения подачи на зуб: Bo>sz (рис. 1б).
Исходное положение режущих кромок сверла (рис. 1б1) - A’oA’o и C’oC’o (Q’o и Оo – воображаемые вершины сверла соответственно при асимметричной и симметричной заточке). При повороте сверла (без рабочей подачи) на 180° соответствующие режущие кромки займут положение A”oA”o и С”oС”o ; новое положение вершины сверла – Q”o . При сравнении положения режущих кромок сверла до и после поворота на 180° определится погрешность заточки сверла в осевом направлении: Bo = C’oА”o .
На рис. 1б2 (сплошными линиями) показано три положения режущих кромок сверла при его перемещении с рабочей подачей: AoAo и СoСo – исходное положение; A1A1 и С1С1 – положение после поворота на 180°;A2A2 и С2С2 – соответственно после поворота на 360°. Здесь: sz = OoO1 = O1O2 – подача на зуб; s = OoO2 – подача сверла.
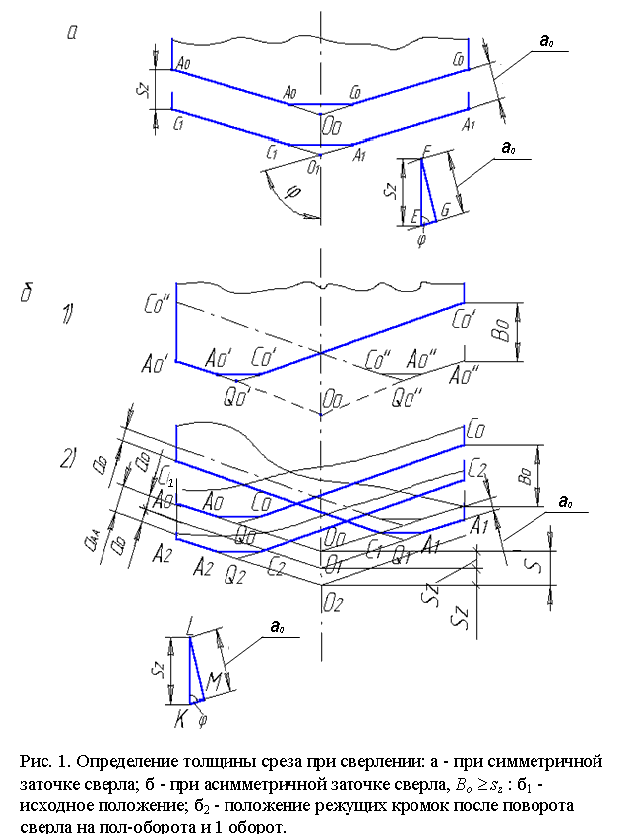
Если бы заточка сверла была строго симметричной, каждое из режущих кромок (AA и СС) снимало бы толщину среза, равную ao . Из анализа положений режущих кромок видно, что вследствие значительной асимметричности заточки сверла резание будет производиться только одной кромкой АА: толщина среза aAA > 0. В это же время вторая кромка (СС) будет оставаться ненагруженной: толщина среза aCC = 0. Таким образом, имеет место случай одностороннего резания. Единственная рабочая режущая
кромка (АА) снимает максимальную (при данной подаче) толщину среза, численно равную удвоенной толщине среза ао для случая симметричного резания: aAA = amax = 2ao . Используя соотношение (1), величина ао может быть определена из треугольника KLM. С учетом этого выражения колебание толщины среза для сверла в целом равно: Δа = aAA - aCC = 2ao ; или
Δao=2szsin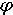 (2)
(2)
Именно возникновение величины Δа > 0 определяет появление не-уравновешенной радиальной составляющей силы резания ΔPy .
Для конкретизации поставленной задачи принят следующий числовой пример. Выполняется сверление отверстия D = 23,6 мм длиной l = 60 мм в чугуне НВ 187 – 196 твердосплавным сверлом общего назначения, имеющим следующие конструктивные параметры: двойной угол при вершине сверла 2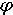 ’ = 118°; радиус сердцевины rc = 0,15r (где r – номинальный радиус сверла); сверло выполнено с плоской передней поверхностью (
’ = 118°; радиус сердцевины rc = 0,15r (где r – номинальный радиус сверла); сверло выполнено с плоской передней поверхностью (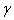 1 = 6°).
1 = 6°).
Прежде всего, проанализируем данные, относящиеся к геометриче-ским параметрам процесса резания (табл. 2).
Таблица 2 – Значения некоторых геометрических параметров сверла
| Ax=rx/r |
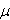 |
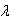 |
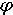 |
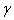 N N |
| 0,183 |
55°03´ |
-44°38´ |
43°38´ |
-29°24´ |
| 0,29 |
31°09´ |
-26°19´ |
54°56´ |
-10°19´ |
| 0,4 |
22°02´ |
-18°45´ |
57°03´ |
-4°47´ |
| 0,5 |
17°27´ |
-14°54´ |
57°48´ |
-2°13´ |
| 0,6 |
14°24´ |
-12°22´ |
58°11´ |
-0°35´ |
| 0,7 |
12°22´ |
-10°35´ |
58°24´ |
0°32´ |
| 0,8 |
10°48´ |
-9°15´ |
58°33´ |
1°22´ |
| 0,9 |
9°36´ |
-8°13´ |
58°39´ |
2°00´ |
| 1,0 |
8°37´ |
-7°23´ |
58°43´ |
2°31´ |
В таблице приняты следующие обозначения анализируемых параметров (помимо вышеуказанных): 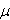 - угол, характеризующий положение произвольной точки режущей кромки сверла (sin
- угол, характеризующий положение произвольной точки режущей кромки сверла (sin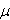 = rc / rx , где rx - текущий радиус произвольной точки режущей кромки);
= rc / rx , где rx - текущий радиус произвольной точки режущей кромки); 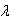 - угол наклона главной режущей кромки;
- угол наклона главной режущей кромки; 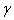 N- передний угол в нормальной секущей плоскости (см. [4]).
N- передний угол в нормальной секущей плоскости (см. [4]).
Для вычисления вышеуказанных углов использованы известные аналитические зависимости [1 - 3]. Анализ данных табл. 2 показывает, что характер изменения этих параметров вдоль режущей кромки сверла коррелирует с известными из литературных источников данными. Значения углов, приведенных в табл. 2, использованы при последующих вычислениях силовых зависимостей при сверлении.
Используя данные [6], для вышеуказанных исходных данных определяем рекомендуемую подачу: s = 0,28 мм/об; следовательно, подача на зуб sz = 0,5s = 0,14 мм/зуб. В то же время, для принятых в примере условий резания допуск осевого биения, определенный по источнику [5], равен Bo = 0,15 мм (см. табл. 1). Так как {Во = 0,15 мм} > {sz = 0,14 мм/зуб}, то имеет место рассмотренный выше случай односто-роннего резания.
Для определения сил резания при сверлении используем метод интегрирования по частям. В этом случае длина режущей кромки условно разбивается на несколько интервалов; в середине каждого из интервалов рассчитывается значение силы резания, а затем производится суммирование по всем интервалам и таким образом находится полная величина искомой силы резания. Для определения сил резания используем аналитические зависимости, приведенные в работе [4]. В частности, радиальная сила резания Py может быть определена из выражения, полученного после соответствующих преобразований аналитических зависимостей, взятых из [4]:
Py=0,9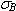 szt*[1+ctg(25°+
szt*[1+ctg(25°+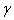 N)]*(20°-
N)]*(20°-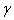 N)*cos(
N)*cos(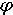 +
+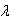 -Δ’) (3)
-Δ’) (3)
где 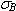 – предел прочности на растяжение обрабатываемого материала; t – глубина резания; Δ´ - вспомогательный расчетный угол.
– предел прочности на растяжение обрабатываемого материала; t – глубина резания; Δ´ - вспомогательный расчетный угол.
При выполнении расчетов режущая кромка сверла условно разделена на 4 интервала. В табл. 3 для каждого из интервалов приведены значения вспомогательных параметров, необходимых для последующих расчетов сил резания. Принятые в табл. 3 обозначения: ΔAxi и ΔbΔi – ширина интервала, выраженная соответственно в долях радиуса сверла и в мм; Δi - угол отклонения стружки.
Таблица 3 – Значения некоторых вспомогательных параметров
| N интервала |
Ax=rx/r |
ΔAxi |
Δbi,мм |
Δi |
| min...max |
Ax,расч |
| 1 |
0,183-0,4 |
0,29 |
0,217 |
2,56 |
-26°47´ |
| 2 |
0,4-0,6 |
0,5 |
0,2 |
2,36 |
-15°26´ |
| 3 |
0,6-0,8 |
0,7 |
0,2 |
2,36 |
-11°07´ |
| 4 |
0,8-1,0 |
0,9 |
0,2 |
2,36 |
-8°46´ |
Значения сил резания, рассчитанные для анализируемого случая, приведены в табл. 4. Принятые обозначения: а - толщина срезаемого слоя;  - угол скалывания; Pz - сила, действующая в направлении главного движения; PN - составляющая силы резания, направленная по нормали к режущей кромке инструмента; Py - радиальная сила резания.
- угол скалывания; Pz - сила, действующая в направлении главного движения; PN - составляющая силы резания, направленная по нормали к режущей кромке инструмента; Py - радиальная сила резания.
Таблица 4 – Определение сил резания
| N интервал |
аi,мм |
 i i |
Pzi |
PNi |
Pyi |
| 1 |
0,2396 |
12°11´ |
570,0 |
367,4 |
53,0 |
| 2 |
0,2586 |
20°17´ |
360,8 |
166,0 |
47,8 |
| 3 |
0,2624 |
23°02´ |
329,0 |
132,8 |
46,4 |
| 4 |
0,2638 |
24°30´ |
314,4 |
117,6 |
45,2 |
|
|
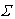 |
1574,2 |
783,8 |
192,4 |
На рис. 2 представлено графическое изображение изменения вдоль режущей кромки сверла взятых из табл. 4 величин толщины среза а и радиальной составляющей силы резания Pyi , что позволяет более наглядно представить характер изменения анализируемых параметров.
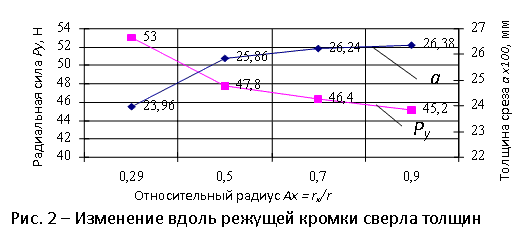
В качестве вывода по работе необходимо указать следующее. Анализ табл. 4 и рис. 2 позволяет выявить следующую закономерность: при перемещении расчетной точки от сердцевины сверла к периферии толщина среза а увеличивается, а составляющие сил резания Pz , PN и Py уменьшаются. Рост толщины среза ai (при неизменной подаче на зуб sz ) вызвано увеличением главного угла в плане 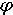 . Уменьшение составляющих сил резанияPz , PN и Py можно объяснить тем, что при соответствующем перемещении расчетной точки возрастает передний угол в нормальной секущей плоскости
. Уменьшение составляющих сил резанияPz , PN и Py можно объяснить тем, что при соответствующем перемещении расчетной точки возрастает передний угол в нормальной секущей плоскости 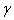 N (см. табл. 2), а следовательно, увеличивается угол скалывания
N (см. табл. 2), а следовательно, увеличивается угол скалывания 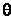 [4], что и приводит к снижению указанных составляющих сил резания.
[4], что и приводит к снижению указанных составляющих сил резания.
При оценке количественных результатов составляющих сил резания а увеличивается, а составляющие сил резания Pz , PN и Py следует иметь в виду следующие обстоятельства. При определении сил резания не учитывались силы, действующие на задние поверхности сверла; а также силы, дополнительно возникающие из-за смещения (эксцентриситета) оси сверла по отношению к оси шпинделя станка. Таким образом, можно предположить, что реальные значения сил резания будут выше сил, определенных расчетом; уточнение этого положения является предметом последующих исследований.
Список литературы:
1. Холмогорцев Ю.П. Оптимизация процессов обработки отверстий. – М.: Машиностроение, 1984. – 184 с.
2. Родин П.Р. Геометрия режущей части спирального сверла. – К.: Техніка, 1971. – 136 с.
3. Семенченко И.И., Матюшин В.М., Сахаров Г.Н. Проектирование металлорежущих инструментов. – М.: Машгиз, 1963. – 952 с.
4. Малышко И.А., Коваленко В.И. Определение неуравновешенной радиальной силы резания при сверлении / Прогрессивные технологии и системы машиностроения: Международный сб. научных трудов. – Донецк: ДонНТУ, 2002, Вып. 19. С. 119-123.
5. Справочник инструментальщика/ И.А. Ординарцев, С.Г. Филиппов, А.Н. Шевченко и др.; Под общ. ред. И.А. Ординарцева. – Л.: Ма-шиностроение. Ленингр. Отд-ние, 1987. – 846 с.
6. Справочник технолога-машиностроителя. В 2-х т. Т. 2/ Под ред. А.Г. Косиловой и Р.К. Мещерякова. – 4-е изд., перераб. и доп.- М.: Маши-ностроение, 1985. - 496 с.


