Коваленко В.И., Федосов Н.Н. (ДонНТУ, г.Донецк, Украина)
Прогрессивные технологии и системы машиностроения: Международный сб. научных трудов. – Донецк: ДонНТУ, 2007, Вып. 33. С.117 - 123.
Проблема точности отверстий, получаемых осевыми режущими инструментами, в том числе сверлами, является актуальной. Уже на стадии проектирования инструмента в ряде случаев необходимо рассчитать величину возможной погрешности, вызываемой инструментом во время работы. Для рациональной эксплуатации осевого режущего инструмента, в частности сверл, требуется их расчет на прочность, а в некоторых случаях (например, при сверлении глубоких отверстий) – также и на устойчивость [1].
При расчете сверл на прочность и устойчивость необходимо знание, в частности, сил резания (определяются по общемашиностроительным справочникам [2] или по специальным методикам [3]) и площадей поперечного сечения сверла. В известной литературе [4 - 6] подобные расчеты выполнены только для сверл, имеющих наиболее употребительные конструктивные характеристики. В то же время в зависимости от конкретных условий обработки могут использоваться нестандартные сверла с конструктивными характеристиками, отличающимися от наиболее употребительных; в этом случае требуется точное определение площади поперечного сечения сверл.
Целью работы является определения площади поперечного сечения сверл, имеющих различные конструктивные особенности. Для достижения поставленной цели необходимо решить следующие задачи: предложить общую методику определения площади поперечного сечения сверл; определить площадь поперечного сечения сверл при постоянном отношении радиуса сердцевины сверла к радиусу сверла; определить площадь поперечного сечения сверл при изменении расчетного се-чения от вершины сверла к хвостовику.
Общая методика определения площади поперечного сечения сверл.
Радиус сердцевины сверла rc определяется в зависимости от радиуса сверла r по выражению
rc=h·r (1)
где h – коэффициент радиуса сердцевины.
На практике сверла выполняют с радиусом сердцевины, увеличивающимся при перемещении расчетного сечения от вершины сверла к хвостовику по всей длине рабочей части; сердцевину увеличивают по направлению к хвостовику для повышения прочности и устойчивости сверл.
При постоянном радиусе сердцевины сверла, его значение в любой точке длины рабочей части определяется по зависимости (1). В этом случае площадь поперечного сечения сверла является функцией от r и h:
S=f(r,h). (2)
Определим значение радиуса сердцевины сверла в расчетном сечении, расположенном в любой произвольной точке вдоль оси сверла (rck).
Введем обозначения:
n = lp/l – коэффициент расчетной длины, где lp – расчетная длина (расстояние от конца режущей части сверла т. О до искомой точки, рис. 1); l - длина рабочей части сверла. Коэффициент n изменяется в пределах n = (0 ÷ 1). Например, n = 0,5 соответст-вует расчетной длине, равной половине общей длины сверла.
kc – коэффициент изменения радиуса сердцевины (радиус сердцевины увеличи-вается на kc мм на каждые 100 мм длины рабочей части сверла).

С учетом введенных коэффициентов, определение значения радиуса сердцеви-ны при его увеличении на определенной длине рабочей части сверла выполняется по следующей зависимости
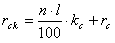 (3)
(3)
Учитывая выражение (3), функциональная зависимость (2) изменится. В этом случае площадь поперечного сечения является функцией от величин r,h,n:
S=f(r,h, n). (4)
Зависимость (4) можно свести к (2) при n = 0, то есть при рассмотрении сечения сверла в точке О (см. рис. 1).
Для стандартных сверл изменение коэффициента радиуса сердцевины колеблется в пределахh= 0,12 ÷ 0,30. В целях исследования влияния радиуса сердцевины на прочность и устойчивость сверл увеличим этот интервал до следующего диапазона значений коэффициента радиуса сердцевины: h = 0 ÷ 1.
Определение площади поперечного сечения сверл при постоянном отноше-нии радиуса сердцевины сверла к радиусу сверла.
Площадь поперечного сечения сверла определим для случая, когда радиус сердцевины постоянен по всей длине рабочей части сверла. Этот вариант подходит и для случая при n = 0; тогда . Полученные зависимости могут быть использованы для этого случая расчета путем подстановки величины rck вместо величины rc.
Общий вид поперечного сечения спирального сверла представлен на рис. 2. Рас-смотрим геометрическое представление элементов стружечной канавки сверла.
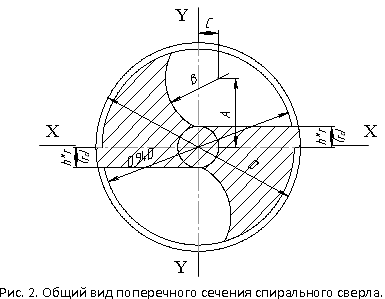
По рекомендациям [5] (см. рис. 2) при радиусе сердцевины rc = 0,2·r радиус ок-ружности канавки B = 0,26D = 0,52r. Центр данной окружности смещен относительно центра сверла на А = 0,33D = 0,66r по оси Y – Y и на C = 0,1D = 0,2r по оси Х – Х.
Сделаем следующие допущения:
- величины А и B изменяются в зависимости от величины радиуса сердцевины по квадратичному закону, а величина C - по линейному;
- при h = 0: А = 0,5∙0.94r = 0,47r, С = 0,25∙0,94r = 0,235r, В = 0,525r;
- при h = 1: А = 0,94r, С = 0, B = 0.
Учитывая вышеприведенные допущения, найдем взаимосвязь между коэффициентом радиуса сердцевины h и величинами А, С, B.
Пусть А =K1 r. Предположим, что
K1=a·h2+b·h+c (5)
Найдем коэффициенты а, b и с:
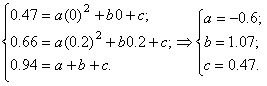 (6)
(6)
Тогда
K1=-0.6h2+1.07h+0.47 (7)
Пусть С = K2 r. Предположим, что
K2=ah+b (8)
Найдем коэффициенты а и b:
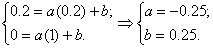 (9)
(9)
Тогда, учитывая выше сказанное, имеем
K2=-0.25h+0.25 (10)
Аналогично, пусть B = K3 r. Предположим, что
K3=ah2+bh+c (11)
Найдем коэффициенты а, b и с:
 (12)
(12)
Тогда
K3=-0.625h2+0.1h+0.525 (13)
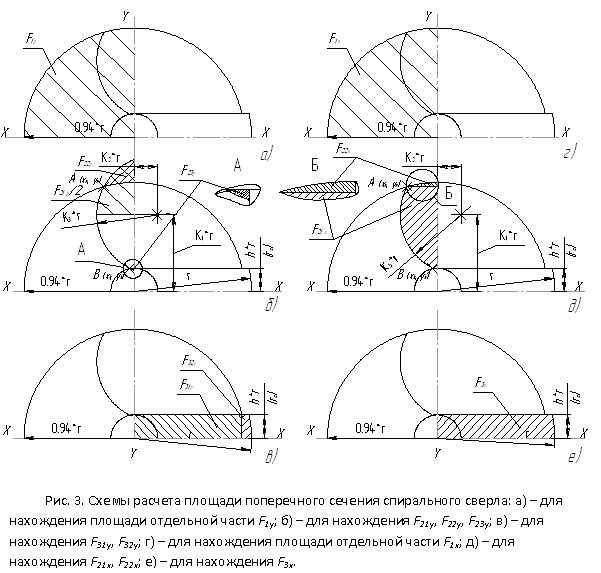
Найдем площадь поперечного сечения спирального сверла с помощью определенного интеграла по оси Y – Y и Х – Х; выведенные зависимости впоследствии будут использованы для определения осевых моментов инерции. Площадь определим по оси Y – Y (рис. 3) по следующей зависимости:
Sy-y=2(F1y-(F21y-F22y-F23y)+(F31y+F32yy)) (14)
где F1y, F21y, F22y, F23y, F31y, F32y – площади простых фигур (см. рис. 3 а, б, в), оп-ределяемых по следующим зависимостям:
 (15)
(15)
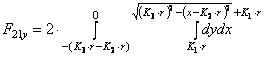 (16)
(16)
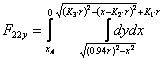 (17)
(17)
 (18)
(18)
 (19)
(19)
 (20)
(20)
где xA – абсцисса точки А(xA; yA) пересечения двух окружностей с радиусами r и B=K3 r; xB – абсцисса точки В(xB; yB) пересечения окружности радиусом B=К3 r и прямой y=hr.
Аналогичным образом определяется площадь сечения спирального сверла по оси X – X (рис. 3 г, д, е).
Выведенные зависимости для определения площади поперечного сечения спирального сверла могут быть использованы при следующих значениях коэффициента радиуса сердцевины (h) и самого радиуса сердцевины (rck), рассматриваемого в любой точке на всей длине рабочей части сверла:
- 0 < h < 0,94,
- rck ≤ r.
С целью уменьшения погрешности вычислений после определения суммарных площадей поперечного сечения сверла относительно осей Y – Y и Х – Х, найдем их усредненные (среднеарифметические) значения
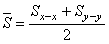 (21)
(21)
Результаты вычислений усредненной площади поперечного сечения для некоторых диаметров сверл (5; 10; 20; 30; 40; 50 мм) из диапазона 5 – 50 мм представлены в табл. 1. Приведенные значения соответствуют исходному сечению сверла, проведенному в точке О (см. рис.1).
Таблица 1. Площадь поперечного сечения спирального сверла в зависимости от отношения rc / r, мм2.
| Диаметр сверла, мм |
Диаметр сверла, мм |
| 0.1 |
0.2 |
0.4 |
0.6 |
0.8 |
0.9 |
| 10 |
29.773 |
35.125 |
47.274 |
59.189 |
68.949 |
72.345 |
| 20 |
119.093 |
140.501 |
189.096 |
236.754 |
275.798 |
289.38 |
| 30 |
267.959 |
316.126 |
425.465 |
532.697 |
620.545 |
651.106 |
| 40 |
476.371 |
562.002 |
756.383 |
947.017 |
1103.191 |
1157.522 |
| 50 |
744.33 |
878.129 |
1181.848 |
1479.714 |
1723.736 |
1808.628 |
Определение площади поперечного сечения сверл при изменении расчетного сечения от вершины сверла к хвостовику.
Рассмотрим случай, когда радиус сердцевины сверла увеличивается по направлению к хвостовику. Например, для сверла диаметром d = 5мм длиной l = 52 мм с от-ношением rc / r = 0.2, радиус сердцевины сверла увеличивается по направлению к хвостовику на 0.85мм на каждые 100мм длины (kc = 0,85).
В табл. 2 представлены результаты вычислений площади поперечного сечения спирального сверла для диапазона диаметров d = 5 – 50 мм, с отношением радиуса сердцевины к радиусу сверла rc / r = 0.2, и при увеличении радиуса сердцевины сверла по направлению к хвостовику на 0,85 мм на каждые 100 мм длины. Для соответствую-щего диаметра указана максимальная длина рабочей части сверла l по ГОСТ 10903-77.. Значения величин площадей определены в сечениях, равноудаленных друг от друга по всей длине рабочей части сверла (n = 0 ÷ 1, шаг 0.2).
Таблица 2. Площадь поперечного сечения спирального сверла при увеличении радиуса сердцевины по направлению к хвостовику, мм2.
| d, мм |
l, мм |
Диаметр сверла, мм |
| 0 |
0.1 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
| 5 |
52 |
8.781 |
8.997 |
9.213 |
9.64 |
10.63 |
10.482 |
10.894 |
| 10 |
87 |
35.125 |
35.849 |
36.57 |
38.004 |
39.426 |
40.835 |
42.23 |
| 20 |
140 |
140.501 |
142.83 |
145.152 |
149.778 |
154.375 |
158.94 |
163.47 |
| 30 |
175 |
316.126 |
320.494 |
324.852 |
333.538 |
342.181 |
350.776 |
359.319 |
| 40 |
200 |
562.002 |
568.659 |
575.303 |
588.553 |
601.747 |
614.881 |
627.95 |
| 50 |
220 |
878.129 |
887.283 |
896.422 |
914.653 |
932.818 |
950.913 |
968.932 |
Выполненные расчеты дают возможность определять площадь поперечного сечения сверл с учетом отношения радиуса сердцевины к радиусу сверлаrc / r и при увеличении радиуса сердцевины сверла по направлению к хвостовику. Приведем пример пользования таблицами 1 и 2.
Предположим, что необходимо определить площадь поперечного сечения сверла, имеющего следующие параметры: диаметр d = 20 мм; общая длина сверла l= 140 мм; расположение расчетного сечения по длине сверла n = 0,5; отношение радиуса сердцевины к радиусу сверла rc / r= 0,2; увеличение радиуса сердцевины сверла по направлению к хвостовику - 0.85 мм на каждые 100 мм длины (kc = 0,85).
По табл. 1 для d = 20 мм и rc / r = 0,2 находим исходную площадь поперечного сечения сверла (в точке О, см. рис.1) S0 = 140,501 мм2. В табл. 2 это же значение соответствует параметрам таблицы: d= 20 мм и n = 0. Далее по табл. 2 находим (интерполируя) искомую площадь поперечного сечения сверла S= 152,1 мм2 для d = 20 мм и n = 0,5.
Выводы.
Результаты выполненной работы дают возможность быстрого определения площади поперечного сечения сверл в диапазоне размеров 5 – 50 мм. Указанное определение площадей возможно как для случая постоянного отношения радиуса сердцевины к радиусу сверла, так и при перемещении расчетного сечения от вершины сверла к хвостовику. Полученные данные необходимы для последующих расчетов сверл на прочность и устойчивость.
Список литературы:
1. Малышко И.А., Коваленко В.И., Кизименко Т.М. К вопросу устойчивости осевого инструмента. Машиностроение и техносфера ХХІ века // Международный сб. научных трудов. – Донецк: ДонНТУ, 2004. Т2. С. 194 - 196.
2. Справочник технолога-машиностроителя. В 2-х т. Т. 2. / Под ред. А.Г. Косиловой и Р.К. Мещерякова. – 4-е изд., перераб. и доп.- М.: Машиностроение, 1985. 496 с.
3. 3. Малышко И.А., Коваленко В.И. Расчет тангенциальной составляющей силы резания при сверлении с учетом соотношения подачи на зуб и осевого биения сверла. Прогресивні технології і системи машинобудування: Міжнародний сб. наукових праць. – Донецьк: ДонНТУ, РВА ДонНТУ, 2005. - Вип. 29. С. 116-121.
4. Сопротивление материалов/Под ред. Писаренко Г.С. – 5-е изд. – К: Вища шк. Голов-ное изд-во, 1986. – 775с.
5. Проектирование металлорежущих инструментов./ Под ред. И.И. Семенченко. – М: Машиностроение, 1963. – 895с.
6. Пономарев С.Д. Основы современных методов расчета на прочность в машиностроении./ М: Машгиз, 1952. – 864с.


