УДК 621.873
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИНАМИКИ ПОДЪЕМА ГРУЗА КРАНАМИ С ПОДВИЖНОЙ КАРЕТКОЙ
Дворников В. И., докт. техн. наук, профессор, Михайлов А.А., студент Донецкий национальный технический университет
 Получены нелинейные дифференциальные уравнения движения при
подъеме груза при одновременном перемещении каретки и крана. Получены нелинейные дифференциальные уравнения движения при
подъеме груза при одновременном перемещении каретки и крана.
 Nonlinear differential equalizations of motion at getting up of load at the simultaneous moving of carriage and faucet are got. Nonlinear differential equalizations of motion at getting up of load at the simultaneous moving of carriage and faucet are got.
 Проблема и ее связь с научными или практическими задачами. Башенные, мостовые и козловые краны с подвижной кареткой подъема груза, схематически изображенные на рис. 1, широко используются в промышленности, строительстве и других отраслях народного хозяйства. Проблема и ее связь с научными или практическими задачами. Башенные, мостовые и козловые краны с подвижной кареткой подъема груза, схематически изображенные на рис. 1, широко используются в промышленности, строительстве и других отраслях народного хозяйства.

Рисунок 1 – Принципиальные схемы башенного, мостового и козлового кранов
 Отличительной особенностью таких кранов является то, что грузовая каретка в общем случае совершает двухмерное движение в горизонтальной плоскости. В связи с этим концевой груз кроме перемещения в вертикальном направлении также перемещается в двух поперечных взаимно перпендикулярных направлениях. В зависимости от принятого режима управления приводами подъемной лебедки, грузовой каретки и ходовых тележек крана концевой груз может интенсивно раскачиваться в поперечных направлениях. Неуправляемые поперечные перемещения груза могут представлять реальную опасность для обслуживающего персонала и окружающих объектов и, как правило, доставляют известного рода неудобства при ведении монтажных и погрузочных работ (так называемая проблема позицирования груза). Отличительной особенностью таких кранов является то, что грузовая каретка в общем случае совершает двухмерное движение в горизонтальной плоскости. В связи с этим концевой груз кроме перемещения в вертикальном направлении также перемещается в двух поперечных взаимно перпендикулярных направлениях. В зависимости от принятого режима управления приводами подъемной лебедки, грузовой каретки и ходовых тележек крана концевой груз может интенсивно раскачиваться в поперечных направлениях. Неуправляемые поперечные перемещения груза могут представлять реальную опасность для обслуживающего персонала и окружающих объектов и, как правило, доставляют известного рода неудобства при ведении монтажных и погрузочных работ (так называемая проблема позицирования груза).
 Анализ исследований и публикаций. Вопрос динамического состояния поднимаемого груза рассмотрен в работах [1, 2, 3]. Динамика подъема при трехмерном перемещении концевого груза ранее не изучалась. Анализ исследований и публикаций. Вопрос динамического состояния поднимаемого груза рассмотрен в работах [1, 2, 3]. Динамика подъема при трехмерном перемещении концевого груза ранее не изучалась.
 Постановка задачи. Целью данного исследования является разработка математической модели трехмерного движения концевого груза при одновременной работе приводов подъемной лебедки, грузовой каретки и ходовых тележек крана. Постановка задачи. Целью данного исследования является разработка математической модели трехмерного движения концевого груза при одновременной работе приводов подъемной лебедки, грузовой каретки и ходовых тележек крана.
 Изложение материала и результаты. Расчетная схематизация процесса подъема груза изображена на рис. 2. Изложение материала и результаты. Расчетная схематизация процесса подъема груза изображена на рис. 2.

Рисунок 2 – Схема подъема груза при горизонтальном перемещении каретки и крана
 Здесь показаны положения поднимаемого груза в двух состояниях: в начальном, когда длина отвеса каната равна l0 (концевая масса сосредоточена в точке B), и в некотором текущем, когда барабан лебедки повернулся на угол φ против хода часовой стрелки, и отвес каната образовал с вертикалью угол θ, отсчитываемый также против хода часовой стрелки, а длина отвеса стала равной l (концевая масса сосредоточена в точке D). Здесь показаны положения поднимаемого груза в двух состояниях: в начальном, когда длина отвеса каната равна l0 (концевая масса сосредоточена в точке B), и в некотором текущем, когда барабан лебедки повернулся на угол φ против хода часовой стрелки, и отвес каната образовал с вертикалью угол θ, отсчитываемый также против хода часовой стрелки, а длина отвеса стала равной l (концевая масса сосредоточена в точке D).
 Как следует из представленной схемы, положение в пространстве точки D в принятой декартовой системе XYZ, определяемое тремя координатами x, y, z, определяется соотношениями: Как следует из представленной схемы, положение в пространстве точки D в принятой декартовой системе XYZ, определяемое тремя координатами x, y, z, определяется соотношениями:
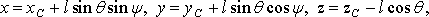 (1) (1)
где xC, yC, zC – текущие координаты точки набегания C, ψ и θ – полярные углы, задающие положение отвеса.
 Считая, что навивка каната на барабан происходит по спирали с шагом h, определим положение в пространстве точки C следующим образом: Считая, что навивка каната на барабан происходит по спирали с шагом h, определим положение в пространстве точки C следующим образом:
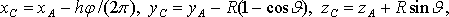 (2) (2)
где xA, yA, zA – текущие координаты неподвижной относительно барабана начальной точки набегания A, R – радиус спиральной навивки каната на барабан, считающимся постоянным, 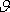 – угол наклона отвеса каната к вертикали в плоскости поперечного сечения барабана, проходящей через точку C. Этот угол, при помощи соотношений (1) определяется как – угол наклона отвеса каната к вертикали в плоскости поперечного сечения барабана, проходящей через точку C. Этот угол, при помощи соотношений (1) определяется как
 (3) (3)
(заметим, что координата ψ в частном случае является циклической).
 В свою очередь, в соотношениях (2) координаты точки A ( xA, yA, zA), а также угол поворота барабана (φ) определяются принятым режимом перемещения каретки вдоль оси X, крана вдоль оси Y и режимом навивки каната при ручном или автоматическом управлении, то есть В свою очередь, в соотношениях (2) координаты точки A ( xA, yA, zA), а также угол поворота барабана (φ) определяются принятым режимом перемещения каретки вдоль оси X, крана вдоль оси Y и режимом навивки каната при ручном или автоматическом управлении, то есть
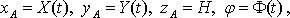 (4) (4)
X(t), Y(t), Φ(t) – некоторые заданные (известные) функции от времени t, H – теоретическая «высота» подъема, равная расстоянию по вертикали от основания крана до оси барабана, как показано на рис. 1 (zA считается постоянной, если стрела или мост крана, а также подкрановый путь имеют строго горизонтальную ориентацию).
 Далее установим взаимосвязь текущей длины отвеса l с введенными координатными углами φ, ψ, θ. Если бы концевая масса не отклонялась от вертикали, и канат представлял бы собой гибкую абсолютно нерастяжимую нить, то, очевидно, Далее установим взаимосвязь текущей длины отвеса l с введенными координатными углами φ, ψ, θ. Если бы концевая масса не отклонялась от вертикали, и канат представлял бы собой гибкую абсолютно нерастяжимую нить, то, очевидно,
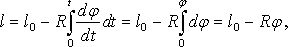 (5) (5)
но при неизбежных отклонениях, главным образом в направлении оси Y, точка набегания каната на барабан (точка C на рис. 2) отклоняется от образующей цилиндра барабана, проходящей через точку A. Следовательно, вместо (5) должно иметь место соотношение
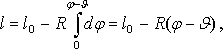 (6) (6)
в котором угол 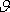 определен выражением (3). Однако в действительности канат является упруго растяжимым стержнем, в силу чего выражение (6) следует записать с учетом (4) в форме определен выражением (3). Однако в действительности канат является упруго растяжимым стержнем, в силу чего выражение (6) следует записать с учетом (4) в форме
 (7) (7)
где δ – упругая продольная деформация каната длиной
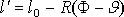 (8) (8)
в результате действия на него статических и динамических нагрузок.
 Обобщая формулы (1), (2), (4) и (7), пространственные координаты поднимаемой массы запишем в виде Обобщая формулы (1), (2), (4) и (7), пространственные координаты поднимаемой массы запишем в виде
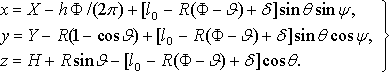 (9) (9)
При этом составляющие вектора скорости на основании (9) представим в форме следующих соотношений
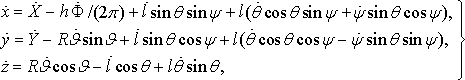 (10) (10)
где точка над символом функции означает производную от этой функции по времени, причем в силу (3)
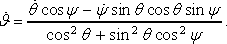 (11) (11)
 Предполагая в дальнейшем применение уравнений Лагранжа второго
рода для описания динамического состояния рассматриваемой системы, ее кинетическую энергию определим как Предполагая в дальнейшем применение уравнений Лагранжа второго
рода для описания динамического состояния рассматриваемой системы, ее кинетическую энергию определим как
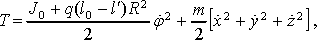 (12) (12)
где φ – текущий угол поворота барабана, определяемый четвертой формулой из (4); q – погонная масса каната; l' определяется соотношением (8); J0 – начальный момент инерции барабана (здесь считается, что текущий момент инерции барабана изменяется за счет присоединенной массы навиваемого на барабан каната); m – масса концевого груза; компоненты абсолютной скорости концевой массы  вычисляются в соответствии с формулами (10). вычисляются в соответствии с формулами (10).
 Потенциальная энергия системы обусловлена изменением положения
концевой массы в гравитационном поле Земли и упругой деформацией каната, в силу чего запишем (см. рис.1 и рис. 2): Потенциальная энергия системы обусловлена изменением положения
концевой массы в гравитационном поле Земли и упругой деформацией каната, в силу чего запишем (см. рис.1 и рис. 2):
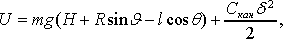 (13) (13)
где Cкан – коэффициент жесткости отвеса каната, определяемый формулой
 (14) (14)
где kП – кратность подъемного полиспаста; E – модуль упругости стали проволоки ( E = 2,06 ×1011 Н / м2 ); a – безразмерный параметр, зависящий от конструкции применяемого каната (для канатов двойной крестовой свивки ГОСТ 7668-80 – a ≈ 0,315 ; для других типов канатов численное значение этого параметра отличается незначительно); dкан – диаметр каната, м; l' определяется соотношением (8).
 Функция Лагранжа L = T - U с учетом (12) и (13), а также с учетом того обстоятельства, что она определена с точностью до слагаемых, представляющих известные функции от времени, будет иметь вид Функция Лагранжа L = T - U с учетом (12) и (13), а также с учетом того обстоятельства, что она определена с точностью до слагаемых, представляющих известные функции от времени, будет иметь вид
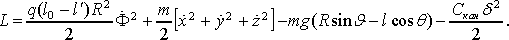 (15) (15)
 В уравнениях Лагранжа В уравнениях Лагранжа
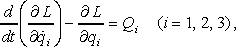 (16) (16)
в качестве обобщенных координат и скоростей дискретных элементов установки целесообразно взять
 (17) (17)
а обобщенные непотенциальные силы - Q1, Q2, Q3 принять равными нулю:
 (18) (18)
так как предполагается, что концевой груз не подвержен действию иных внешних силовых факторов, кроме уже учтенных сил. При более строгом подходе Qi в (16) можно интерпретировать как упруго-вязкие силы сопротивления внешней среды, силы внутреннего трения проволок в канате и др.
 Вычисление в соответствии с (16) частных производных от функции Лагранжа (15) по обобщенным координатам (17) приводит к следующим формальным результатам: Вычисление в соответствии с (16) частных производных от функции Лагранжа (15) по обобщенным координатам (17) приводит к следующим формальным результатам:
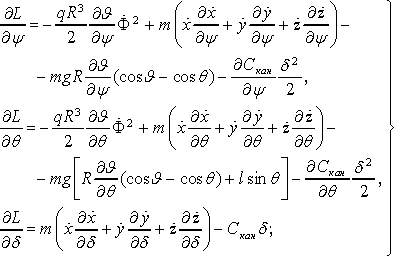 (19) (19)
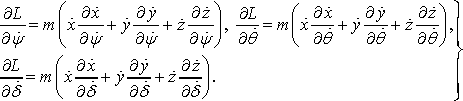 (20) (20)
 В соотношениях (19) в силу обозначения (3) В соотношениях (19) в силу обозначения (3)
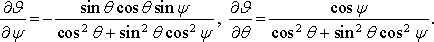 (21) (21)
Кроме того, в соответствии с определением (14) и выражением (8) имеем:
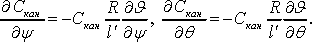 (22) (22)
Что касается остальных частных производных в (19) и (20), то их несложно получить из соотношений (10), однако они здесь не выписаны из-за громоздкости выражений.
 Уравнения динамического состояния поднимаемого груза получим подстановкой (19) и (20) в уравнения Лагранжа (16) с учетом предположения (18) для обобщенных сил: Уравнения динамического состояния поднимаемого груза получим подстановкой (19) и (20) в уравнения Лагранжа (16) с учетом предположения (18) для обобщенных сил:
 (23) (23)
 Выводы и направления дальнейших исследований. Полученная система уравнений относительно полярных углов отвеса каната ψ, θ и упругой деформации каната δ принадлежат к классу нелинейных дифференциальных уравнений, численные решения которых позволят установить рациональные режимы управления приводными механизмами крана для исключения интенсивных колебаний груза. В дальнейшем предполагается рассмотреть автономную, замкнутую систему с регулируемыми электроприводами. Выводы и направления дальнейших исследований. Полученная система уравнений относительно полярных углов отвеса каната ψ, θ и упругой деформации каната δ принадлежат к классу нелинейных дифференциальных уравнений, численные решения которых позволят установить рациональные режимы управления приводными механизмами крана для исключения интенсивных колебаний груза. В дальнейшем предполагается рассмотреть автономную, замкнутую систему с регулируемыми электроприводами.
Список источников
 1. Лобов Н. А. Динамика грузоподъемных кранов. – М.: Машиностроение. – 1987. – 156 с. 1. Лобов Н. А. Динамика грузоподъемных кранов. – М.: Машиностроение. – 1987. – 156 с.
 2. Казак С. А. Динамика мостовых кранов. – М.: Машиностроение. – 1968. – 332 с. 2. Казак С. А. Динамика мостовых кранов. – М.: Машиностроение. – 1968. – 332 с.
 3. Дворников В. И., Геммерлинг В. А. Моделирование динамических процессов в кранах с подвижной кареткой подъема груза. Труды ДонНТУ, вып. 83. – Донецк. – 2004. С. 71-81. 3. Дворников В. И., Геммерлинг В. А. Моделирование динамических процессов в кранах с подвижной кареткой подъема груза. Труды ДонНТУ, вып. 83. – Донецк. – 2004. С. 71-81.
|






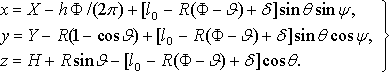 (9)
(9)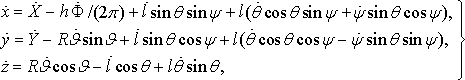 (10)
(10)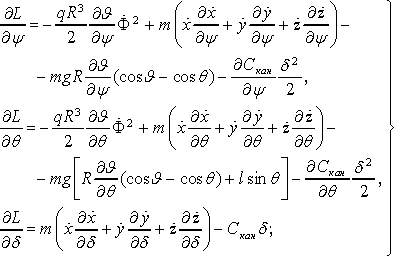 (19)
(19)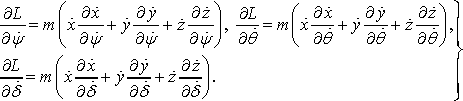 (20)
(20) (23)
(23)