Рудской Денис Станиславович

Факультет: Энергомеханики и автоматизации

Специальность: Подъемно-транспортные, строительно-дорожные, мелиоративные машины и оборудование

Тема выпускной работы:

Анализ и исследование динамического состояния стрелового крана в переходных режимах при подъеме груза

Руководитель: д.т.н. проф. кафедры ГЗТиЛ, Дворников Владимир Иванович

Введение

Грандиозный размах строительства в мире требует постоянного совершенствования средств механизации строительных работ, среди которых важное место занимают стреловые краны. Увеличение грузоподъемности, вылета, высоты подъема, повышение скоростей механизмов современных стреловых кранов приводит к возрастанию динамических нагрузок, действующих на их элементы. Колебательные явления и возникающие при этом динамические нагрузки существенно влияют на прочность и долговечность металлоконструкций, на кинематическую точность рабочих движений, оказывают вредное воздействие на машиниста крана. Поэтому разработка новых высокоэффективных стреловых кранов требует тщательного анализа их динамической нагруженности и дальнейшего совершенствования методов расчета.

Интенсификация погрузочно-разгрузочных работ в строительстве предъявляет высокие требования к надежности каждого грузоподъемного крана, узла и детали, так как отказ в работе любого элемента приводит к простоям основного технологического оборудования, нарушению технологического процесса в целом.

В прямой зависимости от надежности грузоподъемных кранов находится эффективность их использования, которая определяется затратами на их эксплуатацию в виде расходов на оплату труда, обслуживание и ремонты.

Реальные условия работы кранов сопровождаются значительными динамическими перегрузками. Резкое изменение нагрузок на рабочие органы кранов, его механизмы и металлоконструкцию возникает при работе кранов. Поэтому разработка новых высокоэффективных кранов требует тщательного анализа их динамической нагруженности и дальнейшего совершенствования методов расчета.

Общие вопросы динамического расчета машин и механизмов с учетом упругости звеньев достаточно полно освещены в работах А.П. Бессонова, В.Л. Бидермана, В.Л. Вейца, Д.П. Волкова, А.Н. Голубенцева, Ф.К. Иванченко, С.А. Казака, А.Е. Кобринского, С.Н. Кожевникова, М.С. Комарова, С.А. Панкратова, В.П. Терских и др. [2] Большое количество исследований относится к изучению колебательных явлений в грузоподъемных кранах. Главное внимание в этих работах уделяется исследованию переходных процессов и определению динамических нагрузок в элементах кранов.

Исследованиям динамики стреловых кранов посвящены работы И.И. Абрамовича, А.А. Зарецкого, В.Л.. Лифшица, В.В. Момота, Л.А. Невзорова, Н.И. Портного, В.Н. Черенкова, М. Дитриха и др. [2] Преимущественно рассматриваются башенные краны с поворотной башней и подъемной стрелой. Вопросы исследования динамических нагрузок в элементах башенных кранов при повторно-кратковременных режимах работы и при одновременной работе механизмов наиболее полно освещены в работах А.А. Зарецкого. Проведенные на протяжении последних десятилетий теоретические и экспериментальные исследования позволили выработать основные принципы динамического расчета башенных кранов.

Переходные процессы в подъемно-транспортных машинах

Реальные машины и механизмы, как правило, работают по схеме: пуск – разгон до заданной скорости – движение с постоянной скоростью – замедление – стопорение. Далее этот процесс повторяется сколь угодно раз в зависимости от технологического назначения машины. Имеется целый ряд машин, работающих в таком повторно-кратковременном режиме, когда указанный процесс от пуска до стопорения имеет сравнительно небольшую продолжительность и часто повторяется. Примером могут служить подъемно-транспортные машины (краны всевозможных типов), лебедки и подъемные машины, предназначенные для транспортировки различных грузов. В нашем же случае объектом исследования являются стреловые краны [3].

Процессы, происходящие в моменты времени изменения режима движения или работы машины, называются переходными. Разумеется, переходные процессы возникают не только при изменении характера движения, но и при изменении вида внешнего нагружения, при изменении структуры системы и во многих других случаях. Мы же рассмотрим переходные процессы, вызванные только переменностью условий движения

Рисунок 1.1 - К понятию рывка

Анимация состоит из 5 кадров с задержкой 1 с между кадрами; задержка до повторного воспроизведения составляет 5 с; количество циклов воспроизведения - 3

Итак, пусть скорость подъема груза является переменной во времени и управляется либо оператором вручную, либо с помощью специального регулятора по заданной программе.

В простейшем случае, как показано на рис. 1.1, регулируемая скорость изменяется по некоторой ломаной линии .

В физически реальных системах, даже при отсутствии специального регулирования, фактическая скорость, как правило, не имеет резкого излома и между точками 1 и 2, расположенных вблизи точки , изменяется по некоторой плавной дуге, как изображено на рисунке. Происходит это из-за инерционности механизма управления, из-за различного рода задержек и запаздывания сигналов, а также по многим другим причинам.

В большинстве случаев, впрочем, точки 1 и 2 настолько близки к точке , что даже высокочувствительные регистраторы фиксируют это место именно как «излом». Естественно, что в таких случаях в окрестности точки происходит резкое изменение ускорения (или замедления) движения машины. Так, если при движении по линии ускорение равно , то при переходе через точку ускорение практически мгновенно становится равным . Изменение ускорения за единицу времени в механике принято называть рывком, то есть

(1.1)

где , , – соответственно рывок, ускорение и скорость какой-либо специально выбранной для контроля (то есть для управления) точки машины. В дальнейшем перечисленные параметры будут относиться лишь только к этой контрольной или управляемой точке.

Как уже говорилось, в реальности рывок хотя и может достигать больших значений, но все же он ограничен естественными факторами. Искусственное снижение рывка возможно с применением специальных устройств. Системы автоматического управления электроприводом, как правило, основаны на принципе ограничения рывка, и они так и называются – системы подчиненного регулирования с ограничением рывка.

Установим основные зависимости величины рывка от параметров движения с изменяющейся скоростью.

Пусть требуется осуществить плавное изменение скорости в интервале времени такое, чтобы ее вторая производная согласно (1.1) равнялась заданной величине рывка внутри данного интервала. Для этого представим переменную скорость функцией

(1.2)

где и – соответственно скорость и ускорение в точке 1 на рис. 1.1. Как следует из (1.2), функция удовлетворяет условиям сопряжения в точке 1, то есть

но аналогичные условия должны быть и в точке 2 при :

Подстановка сюда выражения (1.2) однозначно приводит к соотношениям:

(1.3)

Путь, пройденный машиной за время , найдем путем интегрирования по функции (1.2) от до :

    (1.4)

Как следует из (1.3), рывок является алгебраической величиной, и его знак определяется знаком разности .

Рассмотрим теперь отвлеченную модель машины, представленную одномерным осциллятором, изображенным на рис. 1.2 (как системы с одной степенью свободы). Такая модель в первом, но в достаточном инженерном приближении описывает подъем груза подъемно-транспортными машинами, подъем стрелы крана. Дифференциальное уравнение такой системы записывается в форме

(1.5)

где применительно к рассматриваемой модели – общая или, как говорят, приведенная к названной выше контрольной точке масса машины; – коэффициент вязкого сопротивления; – жесткость упругой связи; – малая величина деформации упругой связи; – заданный закон движения контрольной (управляемой) точки машины. Дальнейшая задача состоит в назначении такой функции , чтобы как решение уравнения (1.5) обуславливало минимальные напряжения в упругой связи, являющейся основным грузонесущим элементом машины и ответственным за ее безаварийное состояние.

Рисунок 1.2 - Осциллятор с управляемой скоростью спуска-подъема

Пусть точка на рис. 1.2 перемещается так, что вначале она ускоряется, двигаясь вниз, затем некоторое время движется с постоянной скоростью, после чего замедляется и, наконец, останавливается. По истечении времени паузы точка начинает перемещаться в обратном направлении, проходя такие же стадии движения. Затем эти циклы повторяются неоднократно.

Сказанное иллюстрирует диаграмма на рис. 1.3, на которой показано изменение скорости и ускорения точки в течение одного цикла операции спуска-подъема. Здесь рывок в моменты изменения ускорений принят настолько большим, что в точках 0, 1, 2, 3 имеют место резкие «изломы» функции скорости и при этом ускорение изменяется «скачкообразно».

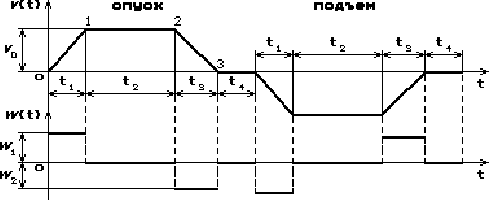
Рисунок 1.3 - Диаграммы скорости и ускорения без ограничения рывка

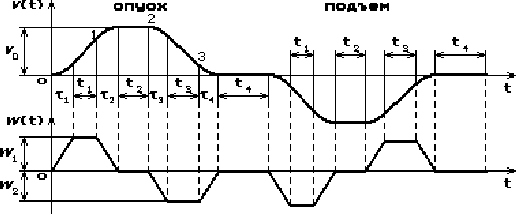
Рисунок 1.4 - Диаграммы скорости и ускорения с ограничением рывка

На рис. 1.4 показано изменение переменной скорости и ускорения точки при достаточно небольших рывках, обеспечивающих плавное изменение скорости в точках 0,1,2,3 (то есть на интервалах , , и ) и трапецеидальный характер изменения ускорений . Функция изменения рывка здесь также не показана, но можно сказать, что она представляет собой ступенчатую линию и отличается от нуля только на интервалах времени , , и , причем согласно с первой формулой (1.3) этим интервалам соответствуют величины рывков, определяемые очевидными соотношениями

(1.6)

в которых знаки рывков обусловлены знаками соответствующих ускорений. В частности, так как (разгон), а (замедление), то , а , разумеется, при естественной положительной определенности .

Знак можно определить также по следующему мнемоническому правилу: если функция на интервале вогнутая, то , а если выпуклая – то

Как правило, в управляемых системах величины являются заданными, как и величины и , и тогда формулы (1.6) могут служить для определения продолжительности интервалов , что также необходимо для возможности интегрирования уравнения движения (1.5). Кроме этого, необходимо определить продолжительности и остальных этапов движения – , , и , а так как интервал (пауза между операциями спуска и подъема) не определяется параметрами движения, а назначается технологическими требованиями, то подлежат определению только три из них – , , . Перед началом вычисления этих интервалов условимся, что помимо параметров , , , , , известными являются еще два параметра – максимальная скорость движения и так называемая высота подъема , которая представляет собой путь движения машины (точки ) от пуска до стопорения.

Интервалы и определяются просто – для этого достаточно в соотношении (1.2) положить , как для равноускоренного движения, и при известных скоростях в начале и в конце интервала вычислить

    (1.7)

Величину можно считать также скоростью в конце интервала , которую определим согласно с (1.2) по формуле

(1.8)

где использовано первое из соотношений (1.6). Скорость же может рассматриваться и как начальная на интервале , а так как в конце этого интервала скорость становится равной , то с помощью (1.2) нетрудно получить

(1.9)

где использовалось второе из соотношений (1.6). Заметим, что здесь , следовательно . Подставив теперь полученные выражения для и в первую формулу (1.7), получим

    (1.10)

Аналогично поступим при определении . Величину можно считать скоростью в конце интервала , и она определяется согласно с (1.2) по формуле

(1.11)

где использовано третье из соотношений (1.6). Скорость же может рассматриваться и как начальная на интервале , а так как в конце этого интервала скорость становится равной нулю, то с помощью (1.2) получим

(1.12)

где использовано четвертое из соотношений (1.6). Подставив теперь полученные выражения для и во вторую формулу (1.7), получим

    (1.13)

Что же касается интервала , то его определим так. Найдем вначале отрезки пути , , , , пройденные машиной соответственно за промежутки времени , , и . Найдем также отрезки пути , , пройденные машиной соответственно за промежутки времени , . А так как общий путь движения машины равен , и на интервале машина движется с постоянной скоростью , то

    (1.14)

Означенные отрезки пути легко находятся по формуле (1.4) с учетом полученных соотношений (1.6). Так,

    (1.15)

С помощью той же формулы (1.4), выражений (1.8), (1.9), (1.11), (1.12), а также соотношений (1.10) и (1.13) найдем, опуская промежуточные выкладки,

    (1.16)

Подстановка (1.15) и (1.16) в (1.14) дает

С помощью найденных выражений для всех интервалов времени несложно записать формулу для суммарного времени движения машины с момента пуска до стопорения в форме

(1.17)

где обозначено

Для интегрирования уравнения движения машины (1.5) теперь можно уже записать:

    (1.18)

где , , ..., – моменты времени, соответствующие началу каждого из означенных на рис. 1.3 интервалов, а именно:

причем последняя отметка времени , где – продолжительность паузы. Заметим, что , определяемое формулой (1.17).

Решение уравнения (1.5), записанное в форме

(1.19)

представляется как сумма решений однородного и неоднородного уравнений, и его несложно получить на любом из означенных интервалов. Затем необходимо потребовать, чтобы на границах каждых соседних интервалов выполнялись равенства этих решений и их первые производные по времени. Такой способ построения решений известен под названием метода сшивания или припасовки. В анализе ограничимся ссылкой на результаты моделирования рассматриваемой системы, представленные на рис. 1.6. Здесь изображены две различные функции , полученные при моделировании операции спуска груза подъемной машиной (кривые 1 и 2). Кривая 1 построена, для варианта, когда все настолько велики, что диаграмма скорости (вверху на рисунке) состоит из одних ломаных линий. Кривая же 2 построена для случая, когда величины рассчитаны по формуле «оптимального рывка»

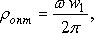
и при этом, как видно, полностью отсутствует колебательный характер функции перемещений. Сама же функция как бы копирует диаграмму ускорения , что и подтверждает сказанное выше.

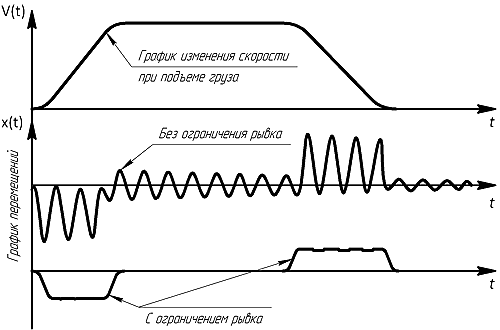
Рисунок 1.5 - Динамические процессы при спуске груза при различных рывках

Анализ изменения динамического состояния груза с применением систем, ограничивающих рывок

На основании теоретических положений был произведен расчет оптимального значения рывка при подъеме груза стреловым краном. Было произведено сравнение поведения динамического состояния машины при различных значениях рывка – без ограничения рывка и с ограничением рывка, рассчитанным соответственно для конкретной подъемной машины с учетом типа каната, его длинны.

Расчет был произведен в программной среде MathCad v.14.0, на основании которого были построены графики как изменения скорости при подъеме груза стреловым краном, так и соответственно ускорения (рис 1.6).

Рисунок 1.6 – Общий вид графика скорости и ускорения груза при подъеме груза

Основой для построения послужила следующая функция:

Временные интервалы t движения груза также рассчитывались исходя из максимальной высоты подъема машины и паспортных значений грузоподъемной машины интегральным методом.

После чего было произведено построение графика изменения скорости для случая без ограничения рывка, т.е. имитация случая без применения специальных средств для ограничения рывка.

Для второго же случая, с ограничением рывка, сперва рассчитывается оптимальное значение рывка, на основании таких значений:

Рисунок 1.7 – К расчету временных интервалов

На основании полученных значений был построен график, отображенный на рис. 1.8 – на котором изображен переходной процесс движения машины при подъеме груза, как с ограничением рывка, так и с его отсутствием. Как видно из графика, с применением ограничения рывка изменение скорости движения груза происходит значительно плавнее, что благоприятно сказывается на общем динамическом состоянии машины – уменьшаются

Рисунок 1.8 – График влияния рывка на скорость машины в момент изменения типа движения

динамические нагрузки на все элементы конструкции подъемной машины, что в достаточной точности отображает рис. 1.5

В дальнейшем планируется исследование данного вопроса более детально, с учетом более широкого ряда значений, основных из которых является учет массы как самого каната, так и других элементов системы подъема груза стреловых кранов.

При написании данного автореферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2009 г. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.

Список использованной литературы

1. Лобов Николай Александрович / Динамика грузоподъемных кранов, М.: Машиностроение, 1987. - 156 с.

2. Гелетий Владимир Николаевич / Разработка динамических моделей и совершенствование расчета башенных кранов. Автореф. дис., (01.02.06). – Львов, 1985. – 18 с.

3. Дворников Владимир Иванович / Конспект лекций по курсу «Динамика строительных машин», Макеевка 2001. - 63 с.

4. Улучшение эксплуатационных характеристик грузоподъемных кранов / Сарадачев, Владимир Иванович, Сердюк, Э.И., Железняк, В.А. – М.: Недра, 1992. – 238 с.

5. Александров М.П. / Подъемно-транспортные машины – М.: Высшая школа, 1985. - 514 с.

6. Ваинсон А.А. / Подъемно-транспортные машины. Машиностроение, 1975. - 431 с.

7. Иванченко Ф.К. / Конструкция и расчет подъемно-транспортных машин. – Киев: Вища школа, 1983. - 351 с.

8. Кузьмин А.В., Марон Ф.Л. / Справочник по расчетам механизмов подъемно-транспортных машин. – Минск: Высшая школа, 1983. - 351 с.