Вступ
 Грандіозний розмах будівництва в світі вимагає постійного вдосконалення засобів механізації будівельних робіт, серед яких важливе місце займають стрілові крани. Збільшення вантажопідйомності, вильоту, висоти підйому, збільшення швидкостей механізмів сучасних стрілових кранів приводить до зростання динамічних навантажень, діючих на їх елементи. явища й виникаючі при цьому динамічні навантаження істотно впливають на міцність і довговічність металоконструкцій, на кінематичну точність робочих рухів, впливають на машиніста крана. Тому розробка нових високоефективних стрілових кранів вимагає ретельного аналізу їх динамічного навантаження і подальшого вдосконалення методів розрахунку.
Інтенсифікація вантажно-розвантажувальних робіт у будівництві висуває високі вимоги до надійності кожного вантажопідйомного крана, вузла й деталі, тому що відмова в роботі будь-якого елемента приводить до простоїв основного технологічного обладнання, порушенню технологічного процесу в цілому.
У прямої залежності від надійності вантажопідйомних кранів перебуває ефективність їхнього використання, що визначається витратами на їхню експлуатацію у вигляді витрат на оплату праці, обслуговування й ремонти.
Реальні умови роботи кранів супроводжуються значними динамічними перевантаженнями. Різка зміна навантажень на робочі органи кранів, його механізми й металоконструкцію виникає при роботі кранів. Тому розробка нових високоефективних кранів вимагає ретельного аналізу їх динамічного навантаження й подальшого вдосконалювання методів розрахунку.
Загальні питання динамічного розрахунку машин і механізмів з урахуванням пружності ланок досить повно освітлені в роботах А.П. Бессонова, Вейца, Д.П. Волкова, А.Н., Іванченко, С.А. Козака, М.С. Комарова, С.А. Панкратова, В.П. і ін. [2] Велика кількість досліджень відноситься до вивчення коливальних явищ у вантажопідйомних кранах. Головна увага в цих роботах приділяється дослідженню перехідних процесів і визначенню динамічних навантажень в елементах кранів.
Дослідженням динаміки стрілових кранів присвячені роботи И.И. Абрамовича, А.А. Зарецького, В.В. Момота, Л.А. Незорова, Н.И. Кравця, М. Дитріха й ін. [2] Переважно розглядаються баштові крани з поворотною вежею й підйомною стрілою. Питання дослідження динамічних навантажень в елементах баштових кранів при повторно-короткочасних режимах роботи й при одночасній роботі механізмів найбільше повно освітлені в роботах А.А. Зарецького. Проведені протягом останніх десятиліть теоретичні й експериментальні дослідження дозволили виробити основні принципи динамічного розрахунку баштових кранів.
Перехідні процеси в підйомно-транспортних машинах
Реальні машини й механізми, як правило, працюють за схемою: пуск – розгін до заданої швидкості – рух з постійною швидкістю – уповільнення – стопоріння. Далі цей процес повторюється може повторюватися багаторазово, залежно від технологічного призначення машини. Є цілий ряд машин, що працюють у такому повторно-короткочасному режимі, коли зазначений процес від пуску до стопоріння має порівняно невелику тривалість і часто повторюється. Прикладом можуть служити підйомно-транспортні машини (крани всіляких типів), лебідки й підіймальні машини, призначені для транспортування різних вантажів. У нашому випадку об'єктом дослідження являються стрілові крани [3].
Процеси, що відбуваються в моменти часу зміни режиму руху або роботи машини, називаються перехідними. Зрозуміло, перехідні процеси виникають не тільки при зміні характеру руху, але й при зміні виду зовнішнього навантаження, при зміні структури системи й у багатьох інших випадках. Ми розглянемо перехідні процеси, викликані тільки змінністю умов руху
Рисунок 1.1 - До поняття ривка
Анімація складається з 5 кадрів із затримкою 1 с між кадрами; затримка до повторного відтворення становить 5 с; кількість циклів відтворення – 3
Отже, нехай швидкість підйому вантажу є перемінною в часі й управляється або оператором вручну, або за допомогою спеціального регулятора по заданій програмі.
У найпростішому випадку, як показано на рис. 1.1, регульована швидкість змінюється по деякій ламаній лінії
 .
У фізично реальних системах, навіть при відсутності спеціального регулювання, фактична швидкість, як правило, не має різкого зламу й між точками 1 і 2, розташованих поблизу точки  , змінюється по деякій плавній дузі, як зображено на рисунку. Відбувається це через інерційність механізму керування, через різного роду затримок і запізнювання сигналів, а також по багатьом іншим причинам.
У більшості випадків, втім, точки 1 і 2 настільки близькі до точки , що навіть високочутливі реєстратори фіксують це місце саме як «злам». Безпосередньо, що в таких випадках в околиці точки відбувається різка зміна прискорення (або уповільнення) руху машини. Так, якщо при русі по лінії  прискорення дорівнює  , то при переході через точку прискорення практично миттєво стає рівним  . Зміна прискорення за одиницю часу в механіку прийнято називати ривком, тобто
(1.1)
де
 ,
 ,
– відповідно ривок, прискорення й швидкість якої-небудь спеціально обраної для контролю (тобто для управління) точки машини. Надалі перераховані параметри будуть стосуватися тільки цієї контрольної
або керованої точки.
Як уже говорилося, у реальності ривок хоча й може досягати великих значень, але все-таки він обмежений природними факторами. Штучне зниження ривка можливо із застосуванням спеціальних пристроїв. Системи автоматичного керування електроприводом, як правило, засновані на принципі обмеження ривка, і вони так і називаються – системи підлеглого регулювання з обмеженням ривка.
Встановимо основні залежності величини ривка від параметрів руху зі швидкістю, що змінюється.
Нехай потрібно здійснити плавну зміну швидкості в інтервалі часу  таку, щоб її друга похідна згідно (1.1) дорівнювала заданій величині ривка усередині даного інтервалу. Для цього представимо змінну швидкість функцією
 (1.2)
де
та
 – відповідно швидкість і прискорення в точці 1 на рис. 1.1. Як слід з (1.2), функція  задовольняє умовам сполучення в точці 1, тобто
але аналогічні умови повинні бути й у точці 2 при  :
Підстановка сюди вираження (1.2) однозначно приводить до співвідношень:
 (1.3)
Шлях, пройдений машиною за час
 , знайдемо шляхом інтегрування по
 функції (1.2) від
 до
 :
 (1.4)
Як слід з (1.3), ривок є алгебраїчною величиною, і його знак визначається знаком різниці  .
Розглянемо тепер відвернену модель машини, представлену одномірним осцилятором, зображеним на рис. 1.2 (як системи з одним ступенем волі). Така модель у першому, але в достатнім інженерному наближенні описує підйом вантажу підйомно-транспортними машинами, підйом стріли крана. Диференціальне рівняння такої системи записується у формі
 (1.5)
де стосовно до розглянутої моделі
 – загальна або, як говорять, приведена до названої вище контрольній точці маса машини;  – коефіцієнт грузлого опору;  – твердість пружного зв'язку;  – мала величина деформації пружного зв'язку;  – заданий закон руху контрольної (керованої) точки машини. Подальше завдання полягає в призначенні такої функції , щоб  як розв'язання рівняння (1.5) обумовлювало мінімальні напруги в пружному зв'язку, що є основним вантажонесучім елементом машини й відповідальним за її безаварійний стан.
Рисунок 1.2 - Осцилятор з керованою швидкістю спуска-підйому
Нехай точка  на рис. 1.2 переміщається так, що спочатку вона прискорюється, рухаючись долілиць, потім якийсь час рухається з постійною швидкістю, після чого вповільнюється й, нарешті, зупиняється. Після закінчення часу паузи точка
починає переміщатися у зворотному напрямку, проходячи такі ж стадії руху. Потім ці цикли повторюються неодноразово.
Сказане ілюструє діаграма на рис.1.3, на якій показане зміна швидкості
 і прискорення  точки протягом одного циклу операції спуска-підйому. Тут ривок у моменти зміни прискорень прийнятий настільки великим, що в точках 0, 1, 2, 3 мають місце різкі «злами» функції швидкості і при цьому прискорення  змінюється «стрибкоподібно».
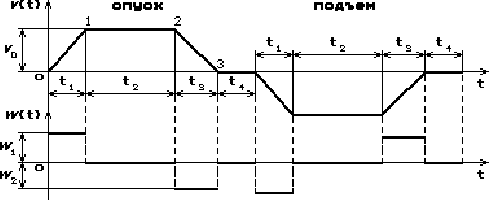
Рисунок 1.3 - Діаграми швидкості й прискорення без обмеження ривка
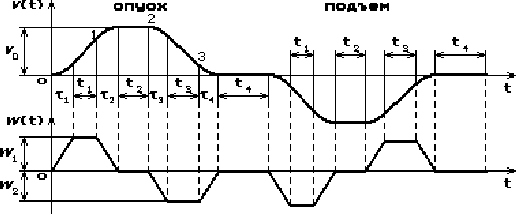
Рисунок 1.4 - Діаграми швидкості й прискорення з обмеженням ривка
На рис. 1.4 показана зміна перемінної швидкості й прискорення точки при досить невеликих ривках, що забезпечують плавну зміну швидкості у точках 0,1,2,3 (тобто на інтервалах
 ,
 ,
 і
 ) і трапецієподібний характер зміни прискорень
.
ункція зміни ривка тут також не показана, але можна сказати, що вона являє собою східчасту лінію й відрізняється від нуля тільки на інтервалах часу
,
,
і
,
причому згідно з першою формулою (1.3) цим інтервалам відповідають величини ривків, обумовлені очевидними співвідношеннями
(1.6)
у яких знаки ривків обумовлені знаками відповідних прискорень. Зокрема, тому що
(розгін), а 
(уповільнення), то  , а
 , зрозуміло, при природній позитивній визначеності  .
Знак
 можна визначити також по наступному мнемонічному правилу: якщо функція на інтервалі увігнута, то  , а якщо опукла - то 
Як правило, у керованих системах величини являються заданими, як і величини і , і тоді формули (1.6) можуть служити для визначення тривалості інтервалів , що також необхідні для можливості інтегрування рівняння руху (1.5). Крім цього, необхідно визначити тривалості й інших етапів руху -  ,
 ,
 і
 , а тому що інтервал (пауза між операціями спуска й підйому) не визначається параметрами руху, а призначається технологічними вимогами, то підлягають визначенню тільки три з них -
,
,
.
Перед початком обчислення цих інтервалів умовимося, що крім параметрів
 ,
 ,
 ,
 ,
,
відомими є ще два параметри - максимальна швидкість руху
 і так звана висота підйому  , що є шляхом руху машини (точки ) від пуску до стопоріння.
Інтервали
і
визначаються просто - для цього досить у співвідношенні (1.2) покласти  , як для рівноприскореного руху, і при відомих швидкостях на початку  і наприкінці інтервалу  обчислити
(1.7)
Величину  можна вважати також швидкістю наприкінці інтервалу , що обумовимо згідно з (1.2) по формулі
(1.8)
де використане перше зі співвідношень (1.6). Швидкість же  може розглядатися і як початкова на інтервалі , а тому що наприкінці цього інтервалу швидкість стає рівної , то за допомогою (1.2) неважко одержати
(1.9)
де використовувалося друге зі співвідношень (1.6). Помітимо, що тут  , отже  . Підставивши тепер отримані вираження для і у першу формулу (1.7), одержимо
(1.10)
Аналогічно надійдемо при визначенні . Величину  можна вважати швидкістю наприкінці інтервалу , і вона визначається згідно з (1.2) по формулі
 (1.11)
де використане третє зі співвідношень (1.6). Швидкість же
 може розглядатися і як початкова на інтервалі , а тому що наприкінці цього інтервалу швидкість стає рівної нулю, то за допомогою (1.2) одержимо
(1.12)
де використане четверте зі співвідношень (1.6). Підставивши тепер отримані вираження для і у другу формулу (1.7), одержимо
(1.13)
Що ж стосується інтервалу , то його визначимо так. Знайдемо спочатку відрізки шляху
 ,
 ,
 ,
 ,
пройдені машиною відповідно за проміжки часу
,
,
и
.
Знайдемо також відрізки шляху
 ,
 ,
пройдені машиною відповідно за проміжки часу
,
. А
А тому що загальний шлях руху машини дорівнює
, и
і на інтервалі
машина рухається з постійною швидкістю
,
то
(1.14)
Зазначені відрізки шляху легко находяться по формулі (1.4) з урахуванням отриманих співвідношень (1.6). Так,
(1.15)
За допомогою тієї ж формули (1.4), виражень (1.8), (1.9), (1.11), (1.12), а також співвідношень (1.10) і (1.13) знайдемо, опускаючи проміжні викладення,
(1.16)
Підстановка (1.15) і (1.16) в (1.14) дає
За допомогою знайдених виражень для всіх інтервалів часу нескладно записати формулу для сумарного часу руху машини з моменту пуску до стопоріння у формі
(1.17)
де позначено
Для інтегрування рівняння руху машини (1.5) тепер можна вже записати:
(1.18)
де
 ,
 ,
...,
 - моменти часу, що відповідають початку кожного із зазначених на рис. 1.3 інтервалів, а саме:
причому остання позначка часу
 ,
де
–
тривалість паузи. Помітимо, що
 ,
обумовлене формулою (1.17).
Рішення рівняння (1.5), записане у формі
(1.19)
представляється як сума рішень однорідного й неоднорідного рівнянь, і його нескладно одержати на кожному із зазначених інтервалів. Потім необхідно зажадати, щоб на границях кожних сусідніх інтервалів виконувалися рівності цих рішень і їхні перші похідні за часом. Такий спосіб побудови рішень відомий за назвою методу зшивання або припасування. В аналізі обмежимося посиланням на результати моделювання розглянутої системи, представлені на рис. 1.6. Тут зображені дві різні функції , отримані при моделюванні операції спуска вантажу підйомною машиною (криві 1 і 2). Крива 1 побудована, для варіанта, коли всі настільки великі, що діаграма швидкості (угорі на рисунку) складається з одних ламаних ліній. Крива ж 2 побудована для випадку, коли величини розраховані по формулі «оптимального ривка»
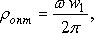
і при цьому, як видно, повністю відсутній коливальний характер функції переміщень. Сама ж функція як би копіює діаграму прискорення  , що й підтверджує сказане вище.
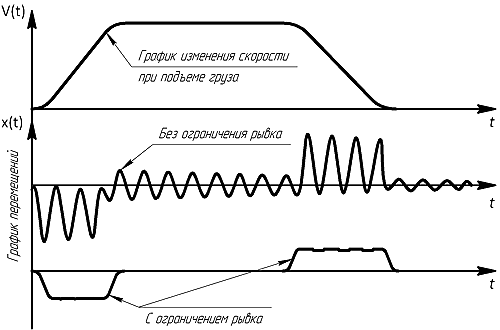
Рисунок 1.5 - Динамічні процеси при спуску вантажу при різних ривках
Аналіз зміни динамічного стану вантажу із застосуванням систем обмеження ривка
На підставі теоретичних положень був зроблений розрахунок оптимального значення ривка при підйомі вантажу стріловим краном. Було зроблене порівняння поводження динамічного стану машини при різних значеннях ривка - без обмеження ривка й з обмеженням ривка, розрахованим відповідно для конкретної піднімальної машини з урахуванням типу каната, його довжини.
Розрахунок був зроблений у програмному середовищі MathCad v.14.0, на підставі якого були побудовані графіки як зміни швидкості при підйомі вантажу стріловим краном, так і відповідно прискорення (рис 1.6).
Рисунок 1.6 – Загальний вигляд графіка швидкості й прискорення вантажу при підйомі вантажу
Основою для побудови є наступна функція:
Тимчасові інтервали t руху вантажу також розраховувалися виходячи з максимальної висоти підйому машини й паспортних значень вантажопідйомної машини інтегральним методом.
Після чого була зроблена побудова графіка зміни швидкості для випадку без обмеження ривка, тобто імітація випадку без застосування спеціальних засобів для обмеження ривка.
Для другого ж випадку, з обмеженням ривка, спершу розраховується оптимальне значення ривка, на підставі таких значень:
Рисунок 1.7 – До розрахунку тимчасових інтервалів
На підставі отриманих значень був побудований графік, відображений на рис. 1.8 - на якому зображений перехідний процес руху машини при підйомі вантажу, як з обмеженням ривка, так і з його відсутністю. Як видно із графіка, із застосуванням обмеження ривка зміна швидкості руху вантажу відбувається значно плавніше, що сприятливо позначається на загальному динамічному стані машини - зменшуються
Рисунок 1.8 – Графік впливу ривка на швидкість машини в момент зміни типу руху
динамічні навантаження на всі елементи конструкції підйомної машини, що в достатній точності відображає рис. 1.5
Надалі планується дослідження даного питання більш детально, з обліком більш широкого ряду значень, основні з яких є облік маси як самого каната, так і інших елементів системи підйому вантажу стрілових кранів.
При написанні даного автореферату магістерська робота ще не завершена. Остаточне завершення: грудень 2009 р. Повний текст роботи й матеріали по темі можуть бути отримані в автора або його керівника після зазначеної вище дати.
Література
1. Лобов Николай Александрович / Динамика грузоподъемных кранов, М.: Машиностроение, 1987. - 156 с.
2. Гелетий Владимир Николаевич / Разработка динамических моделей и совершенствование расчета башенных кранов. Автореф. дис., (01.02.06). – Львов, 1985. – 18 с.
3. Дворников Владимир Иванович / Конспект лекций по курсу «Динамика строительных машин», Макеевка 2001. - 63 с.
4. Улучшение эксплуатационных характеристик грузоподъемных кранов / Сарадачев, Владимир Иванович, Сердюк, Э.И., Железняк, В.А. – М.: Недра, 1992. – 238 с.
5. Александров М.П. / Подъемно-транспортные машины – М.: Высшая школа, 1985. - 514 с.
6. Ваинсон А.А. / Подъемно-транспортные машины. Машиностроение, 1975. - 431 с.
7. Иванченко Ф.К. / Конструкция и расчет подъемно-транспортных машин. – Киев: Вища школа, 1983. - 351 с.
8. Кузьмин А.В., Марон Ф.Л. / Справочник по расчетам механизмов подъемно-транспортных машин. – Минск: Высшая школа, 1983. - 351 с.
|
