1. Введение.

Построение эффективного механизма поиска в коллекциях визуальной информации является одной из наиболее актуальных задач современных научных исследований в сфере компьютерного зрения. Такая задача возникает как при содержательной классификации изображений (к примеру, в медицинской диагностике), так и при контекстном поиске изображений в базах данных (к примеру, при поиске изображений в сети Интернет) [1].

Выделяют следующие основные технологии индексирования изображений в электронных коллекциях [2, 3]:

• индексирование текстовых описаний, ассоциированных с изображениями [2];
• метод цветовых гистограмм [3]. Идея метода цветовых гистограмм для индексирования и сравнения изображений сводится к следующему: все множество цветов анализируемого изображения разбивается на набор непересекающихся, полностью покрывающих его подмножеств. Для изображения формируется гистограмма, отражающая долю каждого подмножества цветов в цветовой гамме изображения. Для сравнения гистограмм вводится понятие расстояния между ними;
• методы поиска по “цветовой планировке” [3, 4]. Отличительной чертой этой группы методов является предварительное разбиение изображений на блоки заданного размера или в заданном количестве. Этот этап позволяет учитывать местоположение того или иного цвета за счет сравнения между собой отдельных блоков, а не всего изображения целиком, что делает методы поиска по “цветовой планировке” более совершенными по сравнению с предыдущей группой методов;
• методы, основанные на кластеризации изображений [4]. При поиске изображений методами этой группы сравнение визуальных примитивов осуществляется на уровне отдельных объектов (регионов, областей) изображений, которые автоматически выделяются в процессе кластеризации на основании подобия значений визуальных характеристик внутри одной области.

Следует отметить, что удовлетворение наибольшего числа запросов возможно при использовании методов, базирующихся на кластеризации, в виду следующих недостатков методов других групп:

• невозможность выделения характеристик формы, текстуры, местоположения объектов изображений без выделения самих объектов [5];
• “чувствительность” к масштабированию, повороту объектов внутри изображений в случае использования группы методов цветовых гистограмм, и к масштабированию – группы методов поиска по “цветовой планировке” [4];
• зависимость результатов поиска от вариации цвета и освещенности изображений [4].

Таким образом, эффективность поиска изображений в электронных коллекциях напрямую связана с эффективностью выделения регионов изображений.

Согласно [4, 6] существует две основные группы методов выделения регионов изображений: статистические методы кластеризации и методы выделения границ объектов путем локализации на изображениях резких перепадов яркости цвета. Однако, методы второй из перечисленных групп более чувствительны к вариации освещенности изображений [4]. Исходя из этого, цель данной работы – разработка нового подхода к использованию статистических методов кластеризации для выделения регионов изображений.

В настоящей работе особое внимание уделено разработке подхода к статистической кластеризации пикселей изображений с учетом специфики объектов кластеризации. Необходимо отметить, что данный подход ориентирован на обработку цветовых характеристик изображений в пространстве с равнозначными составляющими (каждая из составляющих имеет одинаковое влияние на результирующий цвет). В качестве примера такого пространства можно привести пространство RGB.

2. Особенности формирования цветов пространства RGB.

Пусть цвет модели RGB определяется с помощью трех составляющих: R, G, B. Причем, 0≤R≤1, 0≤G≤1, 0≤B≤1 [7].

Возможны следующие основные комбинации, задающие цвет в пространстве RGB.

1. Если числовые значения всех компонентов одинаковые (R=G=B), то результатом является:

• белый цвет (R=G=B=0);
• черный цвет (R=G=B=1);
• серый цвет (если значение больше нуля и меньше единицы: R=G=B, 0<R<1, 0<G<1, 0<B<1).

2. Если числовое значение только одного из анализируемых компонентов больше нуля, то результатом является цвет, которому соответствует ненулевой компонент, степень яркости этого цвета не линейно зависит от значения компонента (чем меньше числовое значение компонента, тем темнее цвет).

3. Если числовые значения двух из трех компонентов больше нуля, то возможны следующие случаи (третий нулевой):

• значения двух компонентов одинаковые, получаем голубой, фиолетовый или желтый цвет, степень яркости которого не линейно зависит от величины ненулевого значения;
• значения ненулевых компонентов неодинаковые. Пусть, к примеру, это будут значения компонентов R и G (R=0.9, G=0.5, B=0.0). Для определения цвета необходимо найти минимум среди ненулевых значений составляющих (для рассматриваемого случая – 0.5), далее рассматривается цвет, получаемый при смешивании ненулевых составляющих с одинаковым числовым значением, которое соответствует найденному минимуму (в общем случае это может быть голубой, фиолетовый или желтый; в нашем примере – желтый), с доминирующим цветом, соответствующем максимальному из значений ненулевых компонентов (в нашем примере – красному). Таким образом, для наших числовых значений цветовых компонентов, имеем смешивание красного и зеленого цветов, результатом которого будет темно-желтый цвет, с дополнением доминирующего красного цвета; т.е. оранжевый цвет.

4. Если числовые значения всех трех компонентов отличны от нуля:

• значения всех компонентов одинаковые – случай 1;
• значения двух из трех компонентов одинаковые, значение третьего компонента меньше значения двух остальных: проводится условное смешивание цветов всех компонентов со значениями, соответствующими минимуму из значений компонентов, получаем серый цвет, степень яркости которого не линейно зависит от найденного минимума, с дополнением цвета смеси компонентов с максимальным числовым значением (голубого, фиолетового или желтого);
• значения двух из трех компонентов одинаковые, значение третьего компонента больше значения двух остальных: проводится условное смешивание цветов одинаковых компонентов, получаем цвет смеси анализируемых цветов (голубой, фиолетовый или желтый), степень яркости которого не линейно зависит от числового значения соответствующих компонентов, с дополнением цвета, соответствующего компоненту с максимальным значением;
• значения всех трех компонентов различные: проводится условное смешивание цветов всех компонентов со значениями, соответствующими минимуму из значений компонентов, получаем серый цвет; проводится условное смешивание компонентов, соответствующих не минимальному значению, с дополнением цвета, соответствующего компоненту с максимальным значением.

В основе предлагаемого метода решения задачи выделения регионов изображений лежит сравнение цветовых характеристик пикселей и объединение пикселей с визуально подобными цветовыми компонентами в кластеры.

Исходя из приведенных выше сведений, можно выделить несколько необходимых (но не достаточных) условий визуального подобия цветов:

1. у визуально подобных цветов не должен отличаться доминирующий цвет (максимальные значения должны соответствовать одной и той же цветовой составляющей);
2. отношения между компонентами подобных цветов должны совпадать (т.е. если для одного пикселя отношения значений соответствующих цветовым компонентам R>G>B, то и для другого пикселя (визуально подобного первому) должны выполняться те же условия между цветовыми компонентами R>G>B);
3. чем меньше величина отличия сравниваемых пикселей по каждой из цветовых компонентов, тем визуально более подобными являются анализируемые цвета.

В зависимости от конкретных изображений выполнение введенных условий может быть более или менее строгим. К примеру, для изображений с объектами в одной цветовой гамме условие может выполняться только для одной пары компонентов (например, только R>G).

3. Битовая маска взаимосвязей и рангов как способ учета особенностей пространства RGB.

Все необходимые условия визуального подобия, отмеченные выше, можно учесть с помощью битовой маски взаимосвязей и рангов цветовых компонентов центров кластеров. Младшие биты битовой маски характеризуют отношения между цветовыми компонентами. При рассмотрении трехмерного цветового пространства и введении трех типов связей (меньше, больше, равно) получаем 9 младших бит. Старшие биты маски описывают уровни каждой из трех характеристик (можно учитывать любое число уровней). Предлагается рассмотреть три основных уровня – низкий, средний и высокий. Для этого весь интервал изменения каждой из цветовых составляющих [x_l, x_h] делится на три равных промежутка – [x_l, GL], (GL, GH], (GH, x_h], соответствующих приведенным уровням. Причем, числовые значения x_l и x_h не связаны с конкретным кластером (или изображением), они определяются исходя из свойств анализируемого цветового пространства. При введении трех уровней имеем 9 старших бит маски.

Таким образом, при рассмотрении трех основных отношений между цветовыми компонентами центров кластеров и трех рангов цветовых компонент предлагаемая битовая маска взаимосвязей и рангов будет состоять из 18 бит.

В качестве цветового пространства выберем пространство цветов RGB, для которого x_l=0 (0), x_h=1 (255).

В таблицах 1, 2 приведены правила формирования старших и младших бит маски для пространства цветов RGB.

Кроме того, предлагается “размывать” границы, как отношений, так и уровней, с помощью введения некоторой погрешности маски – eps.

Таблица 1. Маска рангов компонентов пространства RGB

Старшие биты
Компонент	Предел изменения компонента	Ранг	Маска
B	[xl …GL]	низкий	0 0 0 0 0 0 0 0 1
	(GL…GH]	средний	0 0 0 0 0 0 0 1 0
	(GH… xh]	высокий	0 0 0 0 0 0 1 0 0
G	[xl …GL]	низкий	0 0 0 0 0 1 0 0 0
	(GL…GH]	средний	0 0 0 0 1 0 0 0 0
	(GH… xh]	высокий	0 0 0 1 0 0 0 0 0
R	[xl …GL]	низкий	0 0 1 0 0 0 0 0 0
	(GL…GH]	средний	0 1 0 0 0 0 0 0 0
	(GH… xh]	высокий	1 0 0 0 0 0 0 0 0

Таблица 2. Маска взаимосвязей компонентов пространства RGB

Младшие биты
Компонент	Связь цветовых характеристик	Маска
R и G	R>G	0 0 0 0 0 0 0 0 1
	R=G	0 0 0 0 0 0 0 1 0
	R<G	0 0 0 0 0 0 1 0 0
R и B	R>B	0 0 0 0 0 1 0 0 0
	R=B	0 0 0 0 1 0 0 0 0
	R<B	0 0 0 1 0 0 0 0 0
G и B	G>B	0 0 1 0 0 0 0 0 0
	G=B	0 1 0 0 0 0 0 0 0
	G<B	1 0 0 0 0 0 0 0 0

Приведем анализ рангов цветовых характеристик. К примеру, пусть X₁=x₁, тогда:

• если x₁≤(GL+eps), то Х₁ имеет низкий уровень;
• если x₁≥(GH– eps), то Х₁ имеет высокий уровень;
• если (х₁>(GL– eps) или х₁<(GН+eps)), то Х1 имеет средний уровень.

Кроме того, необходимо так подбирать eps, чтобы было удовлетворено условие: (GL+ eps)<(GН– eps).

В отношении между компонентами X₁ и Х₂ присутствует связь, к примеру “>”, в случае, если удовлетворяется условие X₁ > Х₂; кроме того, предполагается, что если выполняется условие X₁ < (Х₂+ eps), то между X₁ и Х₂ существует и связь “=”. Аналогичными являются рассуждения и для отношения “<”.

Формальное описание построения битовой маски взаимосвязей и рангов кластера с центром {R,G,B} можно записать в следующем виде.

Определим рассматриваемую маску в виде многомерного вектора:

(1)

причем компоненты векторов могут принимать только два значения: 0 или 1.

Условно обозначим вектора рангов 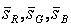вектором , который можно представить как:

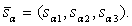(2)

Компоненты вектора определяются по формулам:

(3)

Условно обозначим вектора взаимосвязей вектором , который можно представить в виде:

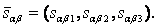(4)

Компоненты вектора определяются по формулам:

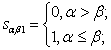, , (5)

В таблице 3 приведены примеры построения битовых масок взаимосвязей и рангов для конкретных числовых значений цветовых составляющих центров кластеров. Предполагается, что значения компонентов R, G и B принадлежат интервалу [0, 1], eps=0.1, GL=0.33 и GH=0.67.

Таким образом, стоит отметить, что как пара компонентов может иметь одновременно две связи (к примеру, больше и равно), так и отдельный компонент может иметь два уровня (к примеру, низкий и средний).

Таблица 3. Примеры битовых масок

Числовые значения центров кластеров			Маска
R	G	B	Биты
			17	16	15	14	13	12	11	10	9	8	7	6	5	4	3	2	1	0
0.5	0.5	0.5	0	1	0	0	1	0	0	1	0	0	1	0	0	1	0	0	1	0
0.7	0.1	0.3	1	1	0	0	0	1	0	1	1	0	1	0	0	0	1	0	0	1
0.2	0.8	1	0	0	1	1	0	0	1	0	0	1	0	0	1	0	0	1	0	0
0.3	0.35	0.9	0	1	1	0	1	1	1	0	0	1	0	0	1	0	0	1	1	0
0.35	0.6	0.3	0	1	1	1	1	0	0	1	1	0	0	1	0	0	1	1	0	0

Разработанная маска применяется как для первоначального разделения пикселей по кластерам, так и в качестве критерия окончания кластеризации статистического иерархического агломеративного алгоритма кластеризации [8]. Рассматривается агломеративная технология, согласно которой, изначально каждый пиксель представляет собой отдельный кластер, для каждого из которых производится расчет битовой маски взаимосвязей и рангов. Затем объекты с одинаковыми битовыми масками образуют новые кластеры, последующее объединение которых производится по Евклидовому расстоянию в цветовом пространстве между центрами кластеров. Такие итерации повторяются до тех пор, пока выполняется условие “сравнимости” анализируемых кластеров. В основе условия “сравнимости” – подсчет числа эквивалентных ненулевых бит масок кластеров, претендующих на объединение.

4. Выводы.

Для построения систем индексации изображений на основе характеристик отдельных кластеров (таких как, характеристики цвета, формы, текстуры) необходимо использование методов кластеризации пикселей изображений, учитывающих специфику объектов кластеризации. Кроме того, иерархические методы и методы группы разбиений не имеют эффективного критерия окончания кластеризации объектов.

Построенная в данной работе маска взаимосвязей и рангов центров кластеров позволяет учесть все приведенные выше ограничения статистических методов кластеризации. В её основе два типа бит – биты взаимосвязей (для учета типов отношений больше, меньше, равно между числовыми значениями составляющих цветового пространства) и биты рангов (для учета уровней числовых значений составляющих цветового пространства).

Литература

1. Chen C.H., Pau L.F., Wang P.S.P. The Handbook of Pattern Recognition and Computer Visions (2nd Edition). – World Scientific Publishing Co., 1998. – 1004 p.
2. Eakins J.P., Graham M.E. A report to the JISC Technology Applications Programе. – Institute for Image Data Research, University of Nothumbria at Newcastle. – 1999. – 54 p.
3. Башков Е.А., Шозда Н.С. Поиск изображений в больших БД с использованием коэффициента корреляции цветовых гистограмм // GraphiCon’2002. – Нижний Новгород. – 2002. – C. 458-460.
4. Wang J. Z., Li J. Wiederhold G. SIMPLIcity: Semantics-Sensitive Integrated Matching for Picture Libraries // IEEE Transactions on Pattern Analysis and Machine Intelligence. – 2001. – vol. 23, №9. – P. 947-963.
5. Karu K., Jain A.K., Bolle R.M. Is There any Texture in the Image? // Pattern Recognition. – 1996. – vol. 29. – P. 1437-1446.
6. Байгарова Н.С., Бухштаб Ю.А., Евтеева Н.Н. Современная технология содержательного поиска в электронных коллекциях изображений. – Институт прикладной математики им. М. В. Келдыша РАН, http://www.artinfo.ru/eva/EVA2000M/eva-papers/200008/Baigarova-R.htm
7. Lansdown J. Visual Perception. – Middlesex: Center for Electronic Arts, 1998. – 157 p.
8. Башков Е.А., Вовк О.Л. Оценка эффективности нового статистического иерархического агломеративного алгоритма кластеризации для распознавания регионов изображений // Системные исследования и информационные технологии. – Институт прикладного системного анализа НАН Украины, Киев. – 2005. – №2. – С. 117-130.