INTRODUCTION

In many machine vision and image processing algorithms simplifying assumption are made about the uniformity of intensities in local image regions. However, images of real objects often do not exhibit region of uniform intensities. For example, the image of a wooden surface is not uniform but contains variations of intensities which form certain repeated pattern called visual texture [1].

Classification of the texture content plays an important role in several image processing applications. Such as medical image analysis, biometric identification, remote sensing, content-based image retrieval, document analysis, environment modeling, texture synthesis and model-based image coding [2].

The accuracy of texture classification depends on the quality of features that are extracted from the analysed image. There are several different groups of features extraction methods [1,3]: statistical, geometrical, structural, model-based, and signal processing techniques. The focus on this paper will be on statistical approaches.

The aim of this article is evaluation of efficacy of three popular statistical texture methods on large textures database. In this connection this work has the following parts: formulation of textures classifications task, statistical features extraction approaches, experiments and results of textures classification.

1 FORMULATION OF TASK

The goal of the texture classification in general is to select the most appropriate category for an unknown object, given a set of known categories [2]. The objects are presented with features vectors that describe their characteristics with numbers.

Classifier techniques have been traditionally divided into two categories [2]: supervised and non-supervised techniques. The first classifiers need some knowledge of the data, be it either training samples or parameters of the assumed feature distributions. With non-supervised techniques, classes are to be found with no prior knowledge. This process is often called clustering.

A supervised classification process involves two phases. First, the classifier must be presented with known training samples or other knowledge of feature distributions. Only after that the classifier can be used in recognizing unknown samples. Prior to the training and the recognition the samples must be processed with the texture analysis method to get a feature vector. The choice of the most efficient statistical method of feature extraction is the aim of this paper.

Examples where texture classification was applied as the appropriate texture processing method include the classification of regions in satellite images into categories of land use [1].

2 STATISTICAL TEXTURE FEATURES

The statistical approach treats the texture as the statistical phenomena. The formation of the texture is described with the statistical properties of the intensities and positions of pixels [2].

It is necessary to remark that color images must be converted to luminance images before these texture features are computed [4]. The conversion rules from color images to luminance images are described in [5,6].

2.1 Co-occurrence Matrices

This method uses the second order statistics to model the relationships between pixels within the image of the texture by constructing the co-occurrence matrix [1,3,5,7].

The co-occurrence matrix is the joint probability occurrence of different gray levels for two pixels with the defined spatial relationship in the image. The spatial relationship is defined in terms of distance r and angle θ. The L*L gray level co-occurrence matrix P is defined as follows [1,5]:

(1)

where:

• i, j – the indexes (gray levels) of matrix P ();
• I(k,s), I(t,v) – the elements of image luminance matrix in positions (k,s) and (t,v) correspondingly;
• r – the distance between elements I(k,s), I(t,v) ( );
• θ – the angle between elements I(k,s), I(t,v) relatively of horizontal axis.

The most commonly used features which are extracted from co-occurrence matrix are presented in Table 1.

Table 1 – The Computation of Co-occurrence Matrix Textures Features

№;	Texture Feature	Formula
1	Energy (angular second moment)
2	Contrast
3	Entropy
4	Correlation

In Table 1:

It is necessary to note that all co-occurrence features are commonly computed for different sets of parameters (r,θ) [5].

2.2 Autocorrelation Features

The autocorrelation method is based on findings of the linear spatial relationships between texture primitives [8]. If the primitives are large (e.g. rock surface), the function decreases slowly with increasing distance whereas it decreases rapidly if texture consists of small primitives (e.g. silk surface). However, if the primitives are periodic, then the autocorrelation increases and decreases periodically with distance.

Formally, the autocorrelation function of the image I is defined as follows [1,5,8]:

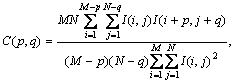
where: p and q is the positional difference in the i, j direction, and M, N are image dimensions.

2.3 Statistical Geometrical Features

The statistical geometrical features algorithm presented in [10] computes statistical measures based on the geometrical properties of connected regions in a series of binary images. These binary images are produced by thresholding operations on the luminance image. Geometrical features like the number of connected regions and their irregularity together with their statistics (mean, standart derivation) describing the stack of binary images are used.

For the image I with L luminance levels the binary image I_Bα can be obtained by thresholding with the threshold value resulting in [11,12]:

For each binary image, all 1-valued pixels are grouped into a set of connected pixel groups termed connected regions. The same is done to all 0-valued pixels.

Let the number of connected regions of 1-valued pixels in the binary image I_Bα be denoted by NOC₁(α), and that of 0-valued pixels in the same binary image by NOC₀(α).

The total number of j-valued pixels (j=0,1) within a region R_i will be called NOP_j(i,α)= | R_i,j |.

To each of the connected regions R_i (of j-valued pixels), the measure of irregularity (un-compactness) is applied, which is defined to be [11,12]:

where

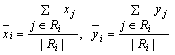
are the centers of mass of the respective region.

The weighted mean irregularity of regions within corresponding binary image is computed as:

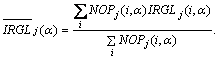
Four function of α i.e. NOC₁(α), NOC₀(α), , , 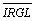have been obtained, each of which is further characterised using four statistics (see Table 2) [10-12].

Table 2 – The Computation of Statistical Geometrical Features

№	Texture Feature	Formula
1	Max value
2	Average value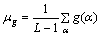
3	Sample mean
4	Sample S.D.

3 EXPERIMENTAL RESULTS

OULU database [13] is used for images classification experiments. Each image has a size of 128*128 pixels and is distributed in BMP format. Seven classes of textures are offered to consider: brick, clouds, grass, leaves, metal, sand, stone. Examples of images of textures are shown in Figure 1.

Figure 1 – The samples of textures classes

Some transformations were applied to original images from database to increase the number of samples available in each class (original class consists of 16 images) and to satisfy criterion of invariant to rotate and scale of images [14]:

• each image was divided into 4 sub-images;
• each image was rotated on 4 angels;
• each image was scaled with 3 scale coefficients.

Finally the test base consists of 1344 images from which texture features are extracted. The features of statistical methods of textures classification are proposed to obtain with the following parameters:

• Co-occurrence matrix method: L=10; r=1,2,3,4; θ=0, π/2, π, 3π/2;
• Autocorrelation method: p=5; q=5;
• Statistical geometrical method: L=5.

The method of supervised textures classification which is proposed in this paper consists of the two following stages :

1) Definition of average features for each group. The results of this stage are shown in Table 3.

2) Classification of all images from the test database is realized by minimal distance between extracted and average features. The different rules of computation distance between groups objects are considered in [15]. In this work the Euclidean distance is used as the measure of similarity between images. In Table 4 the rate of correct textures recognition is shown separately for classification of original images, sub-images, rotated images and scaled images. Thus four criteria of textures classification are described.

Table 3 – The average features for each class

Co-occurrence Matrix (CM)
	Sand	Grass	Brick	Metal	Stone	Clouds	Leaves
Energy	1.921383	9.526959	2.178164	7.086754	2.819481	1.25058	3.994174
Contrast	3.068225	201.544	4.013438	101.4591	9.754948	0.267831	26.10964
Entropy	5.086793	36.98405	6.524425	23.73788	8.49578	1.482942	16.19461
Correlation	-0.349463	-0.05259	-0.3411	-0.07581	-0.24845	-4.12852	-0.13213
Autocorrelation Function (AF)
Max Value	0.927646	0.897977	0.989367	0.891452	0.974844	0.99976	0.956555
Min Value	0.847765	0.81675	0.973531	0.871132	0.965476	0.996583	0.892081
Statistical Geometrical Features (SGF)
Average(NOC0)	44.386719	121.7826	52.38672	272.0729	112.9518	16.94681	57.98828
Max(NOC0)	115.609375	211.5	159.5052	462.2865	278.0729	61.31915	105.9479
Average(NOC1)	26.580729	149.9154	40.27214	158.8763	82.58594	22.59575	49.12109
Max(NOC1)	101.963542	231.8698	121.6615	534.2865	247.9323	86.42553	120.1823
Average(IRGL0)	1.73775	2.120869	2.469744	1.695479	1.644211	1.057186	1.952619
Max(IRGL0)	1.925408	1.975638	3.483693	1.736344	1.884221	1.714998	2.046286
Average(IRGL1)	1.058283	2.401373	1.527258	1.82265	1.727668	1.253473	2.239632
Max(IRGL1)	1.967859	2.557163	1.869386	1.823214	1.858208	1.650004	2.454355

Analyzing the results of experiments it is possible to make the following conclusions:

• SG features are the most suitable features for textures classification because the average total rate of correct classification are the greatest;
• The results of CM and AF methods are less dependent on quantity of tested data than results of SG method (see rows of Table 4 that are depicted recognition rates of original images);
• The class of clouds textures are less visually similar to others classes (for example, the class of metal is visually similar to classes of sand and stone). The results of recognition show that all of tested methods appropriate to computation texture features of those classes but more accurate results are achieved by the methods of the first and second groups.

Table 4 – The Experimental Results of Textures Classification

Co-occurrence Matrix (CM)
Recognition rate (altogether in class	Sand	Grass	Brick	Metal	Stone	Clouds	Leaves	Average rate
Original images (16)	62.5%	81.25%	50%	50%	93.75%	100%	87.5%	75%
Sub-images (64)	54.69%	70.31%	31.25%	51.56%	71.86%	100%	73.44%	64.73%
Rotated images (64)	100%	90.63%	28.13%	53.13%	42.22%	100%	65.63%	68.53%
Scaled images (48)	100%	89.59%	52.08%	41.67%	27.08%	100%	89.59%	71.43%
Total rate (192)	81.77%	82.81%	36.98%	48.44%	51.56%	100%	76.04%	68.23%
Autocorrelation Function (AF)
Original images (16)	56.25%	93.75%	81.25%	50%	93.75%	100%	62.5%	76.79%
Sub-images (64)	50%	84.38%	56.25%	34.38%	96.88%	100%	50%	67.41%
Rotated images (64)	40.63%	29.69%	68.75%	50%	42.22%	100%	65.63%	56.70%
Scaled images (48)	25%	37.5%	77.08%	27.08%	27.08%	100%	48.44%	48.88%
Total rate (192)	42.19%	55.21%	67.71%	39.06%	60.94%	100%	59.90%	60.72%
Statistical Geometrical Features (SG)
Original images (16)	62.5%	37.5%	93.75%	62.5%	37.5%	75%	25%	56.25%
Sub-images (64)	100%	31.25%	75%	31.25%	93.75%	100%	90.63%	74.55%
Rotated images (64)	100%	100%	84.38%	73.44%	100%	96.88%	100%	93.52%
Scaled images (48)	95.83%	100%	93.75%	93.75%	70.83%	97.92%	83.33%	90.77%
Total rate (192)	95.83%	71.35%	84.44%	64.06%	85.42%	96.35%	88.54%	83.71%

CONCLUSION

In this paper three base statistical methods of textures features computation for texture classification were considered. The experimental analysis of investigated methods stability to rotate and scale of the tested images was carried out. The experimental database of textures images contained a total of 1344 samples of seven classes (192 images to class).

The results of experiments show that statistical geometrical methods are the most suitable to depict textures features but those methods have a few restrictions which require additional research. It is also possible to carry out experiments of textures classification by combination of described features.

SUMMARY

In article the base statistic methods of the description of texture features of the images for texture classification are considered. The scheme of experimental estimation of efficacy of textures classification according to each of the methods by criteria of invariant to rotate and scale of textures images are proposed.

REFERENCES

1. Chen C.H., Pau L.F., Wang P.S.P. The Handbook of Pattern Recognition and Computer Vision (2nd Edition), World Scientific Publishing Co., 1998, p.1004.
2. Maenpaa T., The Local Binary Pattern Approach to Texture Analysis – Extensions and application, OULU, 2003, p. 78.
3. Randen T., Husoy J. H., Filtering for Texture Classification: A Comparative Study, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 21, no. 4, April 1999, pp. 291-310.
4. Indexing Color-Texture Image Patterns, Imaging and Vision Laboratory, 2002, http://www.itim.mi.cnr.it/Linee/Linea1/ argomenti/arg3/arg31.htm.
5. Прэтт У., Цифровая обработка изображений. – М.: Мир, 1982. – Кн. 2 – 480 с.
6. Tkalcic M., Tasic J., "Colour spaces: Project for the Digital signal processing course", http://ldos.fe.uni-lj.si/docs/documents/20021113135017_markot.pdf
7. Sharma M., Markou M., Singh S., Evaluation of Texture Methods for Image Analysis, Proc. 7th Australian and New Zealand Intelligent Information Systems Conference, pp. 117-121.
8. Singh M., Singh S., Spatial Texture Analysis: A comparative Study.
9. Sharma M., Performance Evaluation of Image Segmentation and Texture Extraction Methods in Scene Analysis, A thesis for the degree of Master of Philosophy in Computer Science, January 2001, p. 220.
10. Chen Y.Q., Nixon M.S., Thomas D.W., Statistical Geometrical Features for Texture Classification, Pattern Recognition, vol. 28, no. 4, September 1995, pp. 537-552.
11. Munzenmayer C., Volk H., Paulus D., Vogt F., Wittenberg T., Multispectral Statistical Geometrical Features for Texture Analysis and Classification, In K.-H. Franke, editor, 8. Workshop Farbbildverarbeitung, Ilmenau, 2002. Schriftenreihe des Zentrums fur Bild- und Signalverarbeitung e.V. Ilmenau, 1/2002, pp. 87-94.
12. Chen Y.Q., Novel Techniques for Image Texture Classification, A thesis submitted for the degree of Doctor of Philosophy, University of Southampton, March 1995, p. 125.
13. OULU Database, http://www.outex.oulu.fi
14. Wang J. Z., Li J., Wiederhold G., "SIMPLIcity: Semantics-Sensitive Integrated Matching for Picture Libraries", IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 23, no. 9, Sept. 2001, pp. 947-963.
15. Айвазян С. А., Мхитарян В. С. Прикладная статистика и основы эконометрики. Учебник для вузов. – М.: ЮНИТИ, 1998. – 1022 с.