2 СТАТИСТИЧЕСКИЕ МЕТОДЫ

2.1 Матрицы смежности

Статистические методы данной группы используют гистограммные признаки второго порядка для построения модели отношений яркости пикселей рассматриваемого изображения [1,3,5,7].

Пусть матрица компоненты яркости анализируемого изображения – I размером N x M (N – высота, M – ширина изображения). Требуется построить матрицу смежности P (матрицу яркостной зависимости) размером L x L для L квантованных значений яркости рассматриваемого изображения согласно следующему правилу:

(1)

где:

• i, j индексы (уровни яркости) матрицы ();
• I(k,s), I(t,v) – элементы матрицы яркости с координатами (k,s) и (t,v) соответственно;
• r – расстояние между элементами I(k,s), I(t,v) ( );
• θ – угол между элементами I(k,s), I(t,v) относительно горизонтальной оси.

Основные текстурные признаки, которые принято рассчитывать по матрице яркостной зависимости, приведены в таблице 1.

Таблица 1 – Основные текстурные признаки, рассчитанные по матрице зависимости

№	Наименование текстурного признака	Методика расчета
1	Второй угловой момент
2	Контрастность
3	Энтропия
4	Корреляция

В таблице 1:

(2)

Стоит отметить, что матрица P рассчитывается для нескольких наборов значений (r,θ); причем, с точки зрения уменьшения числа вычислительных операций, необходимо ограничить угол и вектор расстояний небольшим количеством дискретных значений.

2.2 Пространственная автокорреляционная функция

С помощью данной функции принято устанавливать относительный размер текстурных примитивов анализируемой текстуры. В области крупнозернистой текстуры значение автокорреляционной функции уменьшается незначительно по сравнению с областью мелкозернистой текстуры.

Формально, в терминах обозначений, введенных в предыдущем подпункте, автокорреляционная функция как [1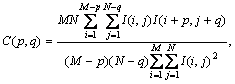3]:

(3)

где: p и q позиционная разница в горизонтальном и вертикальном (соответственно) направлениях изображения..

2.3 Статистические геометрические характеристики

Статистические геометрические признаки текстуры, согласно, основаны на статистических геометрических свойствах соседних регионов бинарного изображения, полученного из анализируемого изображения текстуры.

Для любого изображения текстуры I, бинарное изображение I_Bα получается путем пороговой классификации с пороговым значением согласно правилу [11,12]:

(4)

Для каждого бинарного изображения, все смежные пиксели, имеющие значение «1», группируются в регионы. То же самое действие производится с пикселями - «0». Традиционными являются следующие обозначения:

• NOC₁(α) – число регионов, полученных из пикселей-«1» (регионов-«1»), для бинарного изображения, полученного при пороговом значении α;
• NOC₀(α) – число регионов-“0” полученного при пороговом значении α;
• NOP₁(i,α)=|R_i1| – число пикселей в i-ом регионе-«1»;
• NOP₀(i,α)=|R_i0| – число пикселей в i-ом регионе-«0»;

Меру неравномерности регионов-j (j=0,1) определяют как:

(5)

где

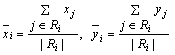(6)

центры тяжести регионов бинарного изображения по координате абсцисс и ординат соответственно.

Взвешенную меру неравномерности регионов соответсвующего бинарного изображения I_Bα можно вычислить по формуле:

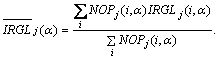(7)

Для каждой из четырех функций NOC₁(α), NOC₀(α), (α), 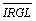(α) предлагается считать статистические текстурные характеристики, приведенные в таблице 2.

Таблица 2 – Вычисление статистическихгеометрических признаков

№	Наименование текстурного признака	Методика расчета
1	Максимальное значение
2	Среднее значение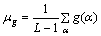
3	Выборочное среднее
4	Выборочное стандартное отклонение

ЛИТЕРАТУРА

1. Chen C.H., Pau L.F., Wang P.S.P. The Handbook of Pattern Recognition and Computer Vision (2nd Edition), World Scientific Publishing Co., 1998, p.1004.
2. Maenpaa T., The Local Binary Pattern Approach to Texture Analysis – Extensions and application, OULU, 2003, p. 78.
3. Randen T., Husoy J. H., Filtering for Texture Classification: A Comparative Study, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 21, no. 4, April 1999, pp. 291-310.
4. Indexing Color-Texture Image Patterns, Imaging and Vision Laboratory, 2002, http://www.itim.mi.cnr.it/Linee/Linea1/ argomenti/arg3/arg31.htm.
5. Прэтт У., Цифровая обработка изображений. – М.: Мир, 1982. – Кн. 2 – 480 с.
6. Tkalcic M., Tasic J., "Colour spaces: Project for the Digital signal processing course", http://ldos.fe.uni-lj.si/docs/documents/20021113135017_markot.pdf
7. Sharma M., Markou M., Singh S., Evaluation of Texture Methods for Image Analysis, Proc. 7th Australian and New Zealand Intelligent Information Systems Conference, pp. 117-121.
8. Singh M., Singh S., Spatial Texture Analysis: A comparative Study.
9. Sharma M., Performance Evaluation of Image Segmentation and Texture Extraction Methods in Scene Analysis, A thesis for the degree of Master of Philosophy in Computer Science, January 2001, p. 220.
10. Chen Y.Q., Nixon M.S., Thomas D.W., Statistical Geometrical Features for Texture Classification, Pattern Recognition, vol. 28, no. 4, September 1995, pp. 537-552.
11. Munzenmayer C., Volk H., Paulus D., Vogt F., Wittenberg T., Multispectral Statistical Geometrical Features for Texture Analysis and Classification, In K.-H. Franke, editor, 8. Workshop Farbbildverarbeitung, Ilmenau, 2002. Schriftenreihe des Zentrums fur Bild- und Signalverarbeitung e.V. Ilmenau, 1/2002, pp. 87-94.
12. Chen Y.Q., Novel Techniques for Image Texture Classification, A thesis submitted for the degree of Doctor of Philosophy, University of Southampton, March 1995, p. 125.
13. OULU Database, http://www.outex.oulu.fi
14. Wang J. Z., Li J., Wiederhold G., "SIMPLIcity: Semantics-Sensitive Integrated Matching for Picture Libraries", IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 23, no. 9, Sept. 2001, pp. 947-963.
15. Айвазян С. А., Мхитарян В. С. Прикладная статистика и основы эконометрики. Учебник для вузов. – М.: ЮНИТИ, 1998. – 1022 с.