В работе предлагается статистический иерархический агломератив-ный алгоритм для выделения подобных областей изображений по цветовым характеристикам. Отличительной особенностью рассматриваемого алгоритма является битовая маска взаимосвязей и рангов цветовых признаков. Также в статье приведены обоснования возможности применения данного алгоритма для кластеризации изображений на регионы.

Введение

Повышенный интерес научных исследователей в сфере компьютерного зрения к анализу оцифрованных изображений делает все более актуальной проблему выделения областей изображений по цветовому подобию. В общем виде данная проблема представляет собой задачу кластеризации – распределения пикселей изображений на несколько групп, однородных по цветовым характеристикам. Полученные группы обычно представляет собой объекты (некоторые области) изображений. Решение такой задачи актуально как при поиске изображений в электронных коллекциях так и при анализе визуальной информации (к примеру, при медицинской диагностике).
Все методы кластеризации изображений можно условно разделить на две группы: статистические методы кластеризации [1] и методы кластеризации, основанные на выделении перепадов яркости [2].
Цель предлагаемой работы – на основании статистических технологий кластеризации  разработать алгоритм выделения значимых областей (регионов, кластеров). В качестве основного применения рассматриваемого в работе алгоритма предполагается контекстный поиск изображений в базах данных [3].

Постановка задачи статистической кластеризации  изображений

При решении проблемы кластеризации каким-либо методом из статистической группы необходимо предварительно представить изображение в виде статистической выборки. После этого над пикселями изображения производятся операции, подобные операциям над элементами выборки.
Кластеризация [4] – общее название множества вычислительных процедур, используемых при создании классификации объектов. В результате кластеризации образуются “кластеры” (регионы, области) – группы похожих по различным характеристикам объектов.
Исходные данные для процедуры кластеризации [4] – набор объектов, каждый из которых задается вектором своих характеристик. В ходе процедуры кластеризации происходит объединение “подобных” объектов в отдельные классы. Результатом кластеризации является набор классов, содержащих однородные объекты.
В случае решения задачи кластеризации изображения задан набор пикселей, каждый из которых определяется тремя цветовыми компонентами в одном из цветовых пространств. С помощью процедуры кластеризации осуществляется выделение групп пикселей, имеющих наиболее “близкие” цветовые компоненты.
Пример выделения регионов (кластеров) изображения приведен на рис. 1.

Рис. 1. Пример кластеризации изображения

Иерархический агломеративный алгоритм кластеризации

На сегодняшний день, по мнению авторов работы, основным недостатком применения статистических методов для выделения однородных областей (регионов) изображений является отсутствие учета “природы” характеристик анализируемых объектов.
В основе предлагаемого алгоритма – битовая маска связей и рангов цветовых компонентов центров кластеров. Так как любое цветовое пространство трехмерно [5], то разработанная маска отражает взаимосвязи и ранги трех цветовых характеристик. Она содержит 18 бит, причем 9 младших бит характеризуют взаимосвязи цветовых составляющих, а старшие 9 бит отражают уровни (ранги) каждого из анализируемых компонентов в отдельности.
При формировании младших бит маски, каждая пара компонентов анализируется на наличие связей типа: меньше, больше и равно.
Старшие биты маски описывают уровни каждой из трех характеристик; вводится три основных уровня – низкий, средний и высокий. Для этого весь интервал изменения каждой из цветовых составляющих [xl, xh] делится на три равных промежутка – [xl, GL], (GL, GH], (GH, xh], соответствующих приведенным уровням.  Причем, числовые значения xl и xh не связаны с конкретным кластером (или изображением), они определяются исходя из свойств анализируемого цветового пространства. Авторами рассматривается пространство цветов RGB, для которого xl=0 (0), xh=1 (255).
В таблицах 1, 2 приведены правила формирования старших и младших бит маски для пространства цветов RGB.

Таблица 1.  Маска рангов компонентов пространства RGB

Старшие биты
компонент	предел изменения компонента	ранг	маска
B	[xl …GL]	низкий	0 0 0 0 0 0 0 0 1
	(GL…GH]	средний	0 0 0 0 0 0 0 1 0
	(GH… xh]	высокий	0 0 0 0 0 0 1 0 0
G	[xl …GL]	низкий	0 0 0 0 0 1 0 0 0
	(GL…GH]	средний	0 0 0 0 1 0 0 0 0
	(GH… xh]	высокий	0 0 0 1 0 0 0 0 0
R	[xl …GL]	низкий	0 0 1 0 0 0 0 0 0
	(GL…GH]	средний	0 1 0 0 0 0 0 0 0
	(GH… xh]	высокий	1 0 0 0 0 0 0 0 0

Таблица 2. Маска взаимосвязей компонентов пространства RGB

Младшие биты
компоненты	связь цветовых характеристик	маска
R и G	R>G	0 0 0 0 0 0 0 0 1
	R=G	0 0 0 0 0 0 0 1 0
	R<G	0 0 0 0 0 0 1 0 0
R и B	R>B	0 0 0 0 0 1 0 0 0
	R=B	0 0 0 0 1 0 0 0 0
	R<B	0 0 0 1 0 0 0 0 0
G и B	G>B	0 0 1 0 0 0 0 0 0
	G=B	0 1 0 0 0 0 0 0 0
	G<B	1 0 0 0 0 0 0 0 0

Кроме того, предлагается “размывать” границы, как отношений, так и уровней, с помощью введения некоторой погрешности маски – eps.
Приведем анализ рангов цветовых характеристик. К примеру, пусть X1=x1, тогда:
если x1<=(GL+eps), то Х1 имеет низкий уровень;
если x1>=(GH– eps), то Х1 имеет высокий уровень;
если (х1>(GL– eps) или х1<(GН+eps)), то Х1 имеет средний уровень.
Кроме того, необходимо так подбирать eps, чтобы было удовлетворено условие: (GL+ eps)<(GН– eps).
В отношении между компонентами X1 и Х2 присутствует связь, к примеру  “>”, в случае, если удовлетворяется условие X1 > Х2; кроме того, предполагается, что если выполняется условие X1 < (Х2+ eps), то между X1 и Х2 существует и связь “=”. Аналогичными являются рассуждения и для отношения “<”.
Таким образом, стоит отметить, что как пара компонентов может иметь одновременно две связи (к примеру, больше и равно), так и отдельный компонент может иметь два уровня (к примеру, низкий и средний).
Разработанный иерархический агломеративный алгоритм предназначен для кластеризации изображений в трехмерном цветовом пространстве RGB (т.е. для каждой точки изображения вектор характеристик содержит свойства красного, зеленого и синего компонентов) и состоит из двух основных этапов.
1. Этап полной связи. Предполагается, что изначально каждый пиксель изображения представляет собой отдельный кластер (свойство агломеративности); на этом шаге происходит группировка точек изображения в кластеры с одинаковыми битовыми масками. Т.е. для каждого пикселя изображения формируется маска взаимосвязей и рангов, затем пиксели с различными масками разносятся в разные кластеры (соответственно, кластеры с одинаковыми масками объединяются в один кластер). Данный этап предназначен для ускорения процесса кластеризации изображения. Для формального описания рассмотренного этапа введем следующие классы, переменные и методы:
класс Cluster (описание его переменных и методов – рис. 2.);
класс Color, объекты которого отражают цветовые характеристики в пространстве RGB;
ArrMask – массив битовых масок взаимосвязей и рангов кластеров. Для данного массива предполагается наличие методов Добавить(маска элемента) и Удалить(маска элемента) элемент;
ArrColors – массив цветов анализируемого изображения, элементы массива типа Color;
Np – количество точек анализируемого изображения;
ArrCluster – массив кластеров изображения, элементы массива типа Cluster. Для данного массива предполагается наличие методов Длина(), Добавить(кластер), Удалить(кластер), ПоискМаски(маска кластера). Последний  метод предполагает возращение булевого результата ({Да, Нет}) – есть ли в массиве элемент с заданной параметром маской;
CurrMask – рассматриваемая маска;
CurrCluster – текущий кластер (объект типа Cluster);
i, j – переменные цикла.

Рис.2. Описание класса Cluster

Упрощенная блок-схема этапа приведена на рис. 3.

Рис.3. Блок-схема этапа полной связи

Этап одиночной связи. Для полученных на предыдущем этапе кластеров строится матрица близости (расстояний) между кластерами. В качестве расстояния между кластерами используется среднее Евклидово расстояние между всеми парами точек, входящих в кластеры, расстояние между которыми рассчитывается. В полученной матрице происходит поиск наиболее “близких” кластеров (т.е. минимумов матрицы близости). Если расстояния между несколькими парами кластеров являются одинаковыми и минимальными, то, в первую очередь, в качестве “близких” кластеров, выбираются кластеры с минимальной площадью. Найденные “близкие” кластеры объединяются, образуя новые кластеры, для которых производится перерасчет центров. Из матрицы расстояний удаляются строки и столбцы, соответствующие объединенным кластерам, и добавляется строка и столбец, соответствующие полученному кластеру. Причем, объединение кластеров с минимальным расстоянием матрицы близости производится только при выполнении условия “сравнимости” масок кластеров; в противном случае процесс кластеризации заканчивается. Обозначим маски кластеров,  претендующих  на  объединение – M1 и М2. Тогда основные стадии анализа выполнения условия “сравнимости” масок следующие:
расчет результирующей маски объединения: Mr=M1&M2 (& – побитовое умножение);
установка начального значения количества эквивалентных бит анализируемых масок: Kb=0;
анализ всех соответствующих триад масок Mr, M1 и М2 в отдельности:
Если ((Mr & 7) И  НЕ((M1 & 2 ИЛИ M2 & 2)  И
                         ((M1 & 4 И M2 & 1) ИЛИ (M2 & 4 И M1 & 1))))
То Kb= Kb+1
переход к следующей триаде масок: Mr= Mr>>3, M1= M1>>3 и M2= M2>>3;
возращение к анализу следующей триады масок.
анализ полученного числа эквивалентных битов:
Если (Kb>=Kopt) (Kopt подбирается экспериментально)
То  условие “сравнимости” масок выполняется;
Иначе условие “сравнимости ” масок не выполняется.
Т.е. при анализе триад масок количество эквивалентных бит инкрементируется, если конъюнкция масок кластеров содержит хотя бы одну единицу (Mr & 7), причем пара триад рассматриваемых масок не должна быть двух следующих типов (НЕ ((M1 & 2 ИЛИ M2 & 2) И ((M1 & 4 И M2 & 1) ИЛИ (M2 & 4 И M1 & 1)))): 1) (1 1 0) и (0 1 1); 2) (0 1 1) и (1 1 0).
            Для наглядного описания этапа одиночной связи c помощью блок-схемы (рис. 4) кроме обозначений, введенных для описания предыдущего этапа, необходимо описание следующих:
D – матрица расстояний между кластерами, для которой предполагается наличие методов: ОбъединениеКластеров(индекс кластера1, идекскластера2) (в основе метода – удаление строк и столбцов матрицы, соответствующих кластеру1 и кластеру 2, добавление новой строки и столбца, соответствующих кластеру, полученному в результате объединения кластера 1 и кластера2; соответствующие изменения происходят и массиве ArrCluster), ПоискМинимумов(нижний предел минимума) (возвращает массив минимумов матрицы D, элементы которой являются координатами строк и столбцов минимальных элементов; при поиске диагональные элементы не рассматриваются – они нулевые; нижний предел отражает границу, выше которой минимумы анализируются, необходим для рассмотрения минимумов только между “сравнимыми” кластерами). Элементы матрицы D (с учетом обозначений введенных выше) рассчитываются как:

(1)

ArrMins – массив минимумов матрицы D. Предполагается наличие методов: Длина(), ПоискМинимальнойПлощади() (возвращает координаты того минимума, который соответствует кластерам с минимальной площадью);
Хmin, Ymin – координаты кластеров с минимальной площадью;
Mingr – нижняя граница минимумов (для функции ПоискМинимумов(нижняя граница) в матрице расстояний);
Comparable – признак “сравнимости” кластеров (булевского типа).

Экспериментальное обоснование возможности применения иерархического агломеративного алгоритма для выделения регионов изображений

Согласно [6] при качественной кластеризации изображений с помощью некоторого алгоритма: энтропия кластеризированных изображений должна возрастать с возрастанием количества выделенных кластеров. Экспериментальное тестирование авторами работы проводилось на базе данных из 1000 24-битных изображений, доступной на [7]. При тестировании экспериментально были подобраны следующие значения параметров анализируемого алгоритма: eps=0.05, Kopt=6.
 Результаты эксперимента, удовлетворяющие приведенному выше положению, приведены на рис.5.  

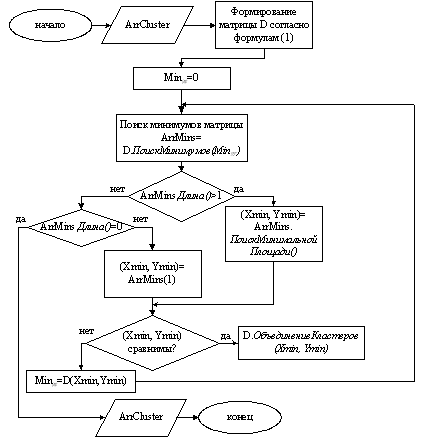
Рис.4. Блок-схема этапа одиночной связи

Рис.5. Зависимость энтропии изображений от числа кластеров

Заключение

В работе предлагается применение статистического иерархического агломеративный алгоритма кластеризации для выделения отдельных регионов изображений. Особенностью описываемого алгоритма является введение битовой маски взаимосвязей и рангов, которая позволяет учитывать особенности кластеризируемых объектов. Также в статье предлагается одно из возможных обоснований возможности использования предлагаемого алгоритма для выделения кластеров изображений. Как дальнейшее направление работы можно выделить проверку устойчивости предлагаемого алгоритма к различным искажениям.

 

Литература

1. Chen C.H., Pau L.F., Wang P.S.P. The Handbook of Pattern Recognition and Computer Vision (2nd Edition). – World Scientific Publishing Co. – 1998. – 1004 p.
2. Байгарова Н. С., Бухштаб Ю. А., Евтеева Н. Н. Современная технология содержательного поиска в электронных коллекциях изображений. – Институт прикладной математики им. М. В. Кел-дыша РАН, http://artinfo.ru/eva/eva2000M/eva-papers/200008/Baigarova-R.htm.
3. Вовк О.Л. Поиск изображений в электронных коллекциях на основе регионального разбиения // САИТ-2003. – Киев. – 2003. – с. 144-145.
4. Ким Д.О., Мьюллер Ч.У., Клекка У.Р. Факторный, дискриминантный и кластерный анализ. – М.: Финансы и статистика. – 1989. – 215 с.
5. Прэтт У. Цифровая обработка изображений. – М.: Мир. – 1982. – Кн. 1 – 312 с.
6. Chen Y., Wang J.Z., Li J. FIRM: Fuzzily Integrated Region Matching for Content-based Image Retrieval // Proc. ACM Multimedia. – Otta-wa. – September, 2001. – P. 543-545.
7. База данных изображений, http://wang.ist.psu.edu/~jwang/test1.tar.